SDE 在生成模型中的统一作用

SDE 统一视角

​ 在之前的文章中，我们介绍了 score-based model 的基本概念，包括其如何对数据分布进行建模、如何从建模的分布中采样，以及通过对分布施加扰动来提高建模精度的方法。本文将重点探讨如何运用随机微分方程（Stochastic Differential Equations, SDEs）来构建和理解 score-based 生成模型。

​ SDE 提供了一个强大的数学框架，能够将 score-based model 和 DDPM (Denoising Diffusion Probabilistic Models) 等看似不同的模型统一起来。尽管基于 SDE 构建扩散模型引入了新的视角，但其核心思想依然围绕着 score function。

随机微分方程简介

​ 首先，我们回顾一些随机微分方程的基础知识。作为对比，我们先看一个常微分方程（Ordinary Differential Equation, ODE）的例子：

$$\frac{d\boldsymbol x}{dt} = f(\boldsymbol x, t) \quad \text{or} \quad d\boldsymbol x = f(\boldsymbol x, t) dt$$

其中 $f(\boldsymbol x, t)$ 描述了向量 $\boldsymbol x$ 随时间 $t$ 的变化规律。该 ODE 的解析解为：

$$\boldsymbol x(t) = \boldsymbol x(0) + \int_0^t f(\boldsymbol x, \tau) d\tau$$

在实际计算中，我们通常无法得到解析解，而是采用数值方法（如前向欧拉法）进行迭代逼近：

$$\boldsymbol x(t + \Delta t) \approx \boldsymbol x(t) + f(\boldsymbol x(t), t) \Delta t$$

​ ODE 描述的是确定性过程。然而，许多现实世界的过程（例如从复杂分布中采样）本质上是随机的，这时就需要随机微分方程（SDE）来进行描述。SDE 在 ODE 的基础上引入了一个随机噪声项：

$$\frac{d\boldsymbol x}{dt} = \underbrace{f(\boldsymbol x, t)}_{漂移项(drift)} + \underbrace{g(t) \boldsymbol w_t}_{扩散项(diffusion)} \quad \text{or} \quad d\boldsymbol x_t = f(\boldsymbol x_t, t) dt + g(t) d\boldsymbol w_t$$

​ 其中：

• $f(\boldsymbol x, t)$ 称为漂移系数（drift coefficient），描述了 $\boldsymbol x_t$ 的确定性趋势。
• $g(t)$ 称为扩散系数（diffusion coefficient），控制随机扰动的强度。
• $\boldsymbol w_t$ 表示标准布朗运动（Brownian motion），也称为维纳过程（Wiener process）。它是驱动随机性的核心，具有以下关键性质：
  1. 独立增量：对任意时间 $s < t < u < v$，增量 $\boldsymbol w_t - \boldsymbol w_s$ 和 $\boldsymbol w_v - \boldsymbol w_u$ 是独立的。
  2. 正态增量：增量 $\boldsymbol w_{t+\Delta t} - \boldsymbol w_t$ 服从均值为 $\boldsymbol 0$、协方差矩阵为 $\Delta t \cdot I$ 的正态分布，即 $\boldsymbol w_{t+\Delta t} - \boldsymbol w_t \sim \mathcal{N}(\boldsymbol 0, \Delta t \cdot I)$。
  3. 连续而不可导：$\boldsymbol w_t$ 的样本路径几乎处处连续，但几乎处处不可导。

​ $d\boldsymbol w_t$ 的积分（如伊藤积分）用于建模随机波动对系统动态的累积影响。与 ODE 类似，SDE 也可以通过数值方法进行迭代求解，例如使用欧拉-丸山（Euler-Maruyama）法：

$$\boldsymbol x(t + \Delta t) \approx \boldsymbol x(t) + f(\boldsymbol x(t), t) \Delta t + g(t) \sqrt{\Delta t} \boldsymbol z_t$$

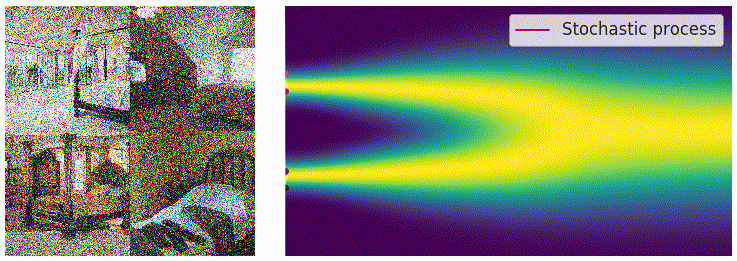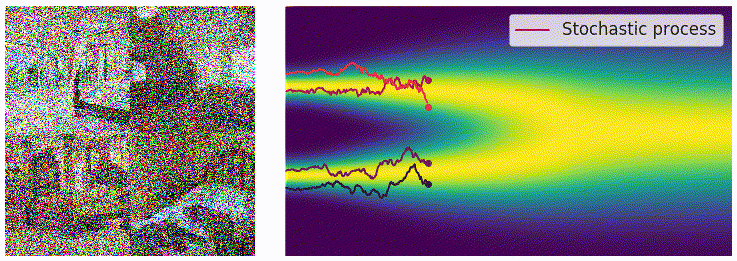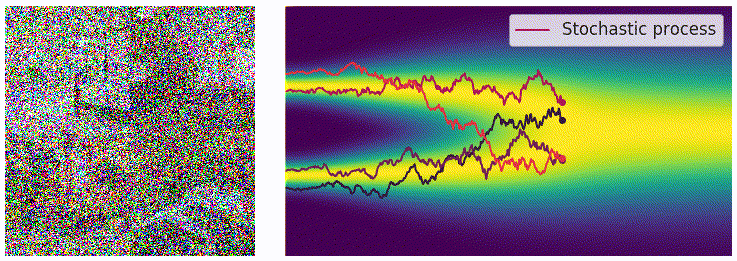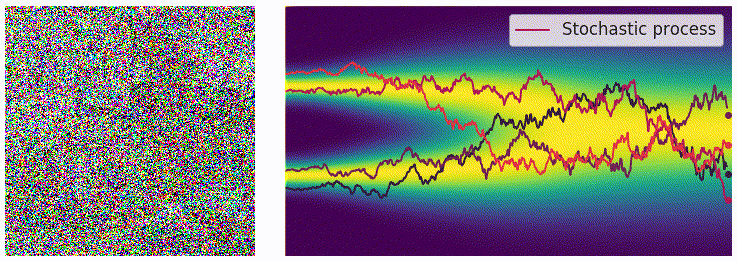
其中 $\boldsymbol z_t \sim \mathcal{N}(\boldsymbol 0, I)$ 是一个标准高斯随机向量。由于采样过程中存在高斯噪声，对同一个 SDE 进行多次数值求解会得到不同的样本路径，如下图右侧所示的一系列绿色折线。

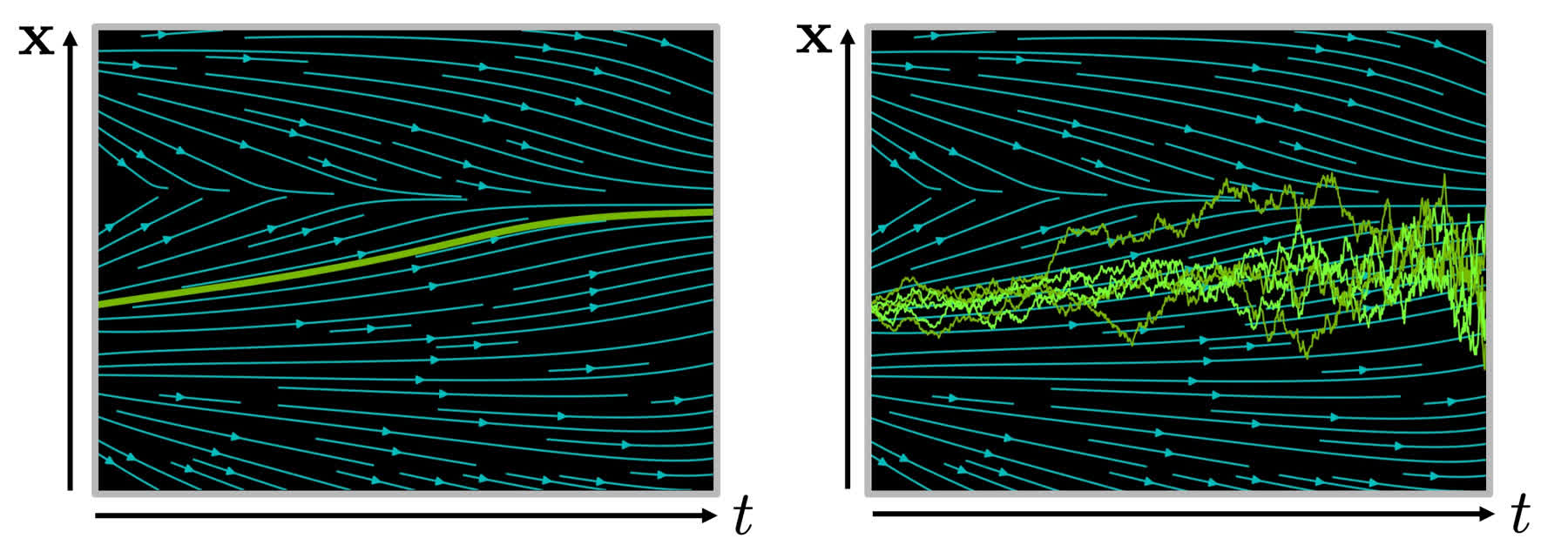
左：ODE 的确定性轨迹。右：SDE 的多条随机轨迹。

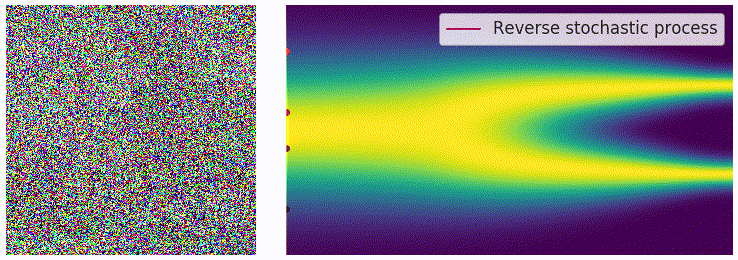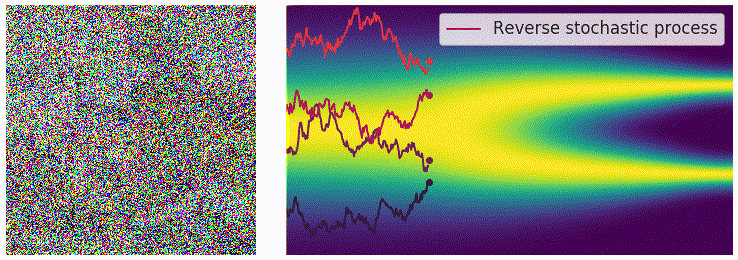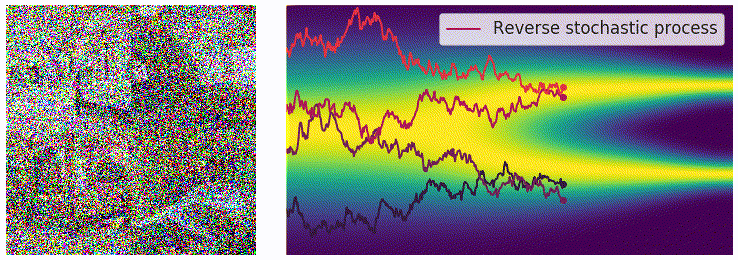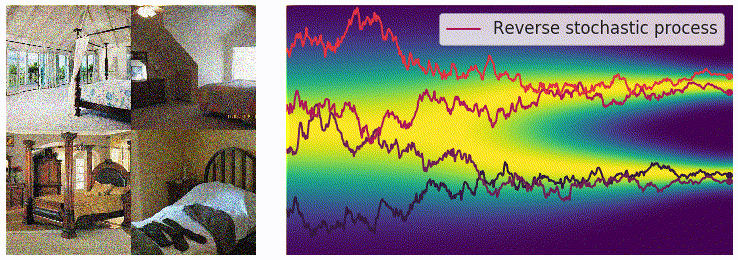
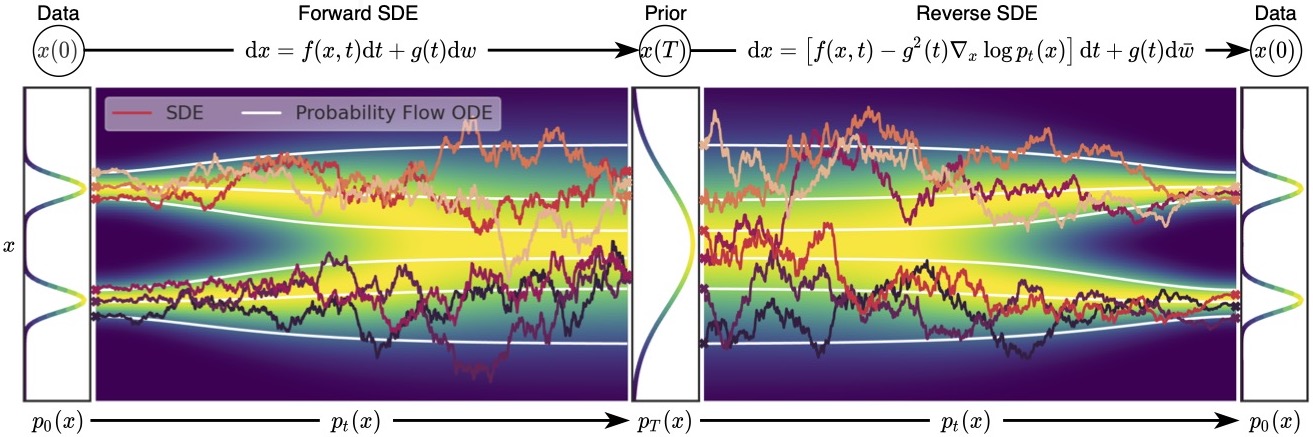
​ 一个非常关键的结论是（不加证明地给出，数学家干的事情），对于一个由上述 SDE 定义的前向过程（forward process），其时间反向过程（reverse process）也同样由一个 SDE 描述。若前向 SDE 和反向 SDE 满足：

$$d\boldsymbol x = f(\boldsymbol x,t)dt + g(t)d\boldsymbol w \\ d\boldsymbol x = \left[ f(\boldsymbol x,t) - g^2(t) {\color{red} \nabla_{\boldsymbol x} \log p_t(\boldsymbol x)} \right] dt + g(t)d\overline{\boldsymbol w}$$

其中 $d\overline{\boldsymbol w}$ 表示反向的布朗运动，$p_t(\boldsymbol x)$ 是 $\boldsymbol x(t)$ 在时刻 $t$ 的概率密度函数。通常，我们设定 $t=0$ 对应于真实数据分布 $p_0(\boldsymbol x) = p_{\text{data}}(\boldsymbol x)$，$t=T$ 对应于一个已知的先验分布（如标准高斯分布 $p_T(\boldsymbol x) \approx \mathcal{N}(\boldsymbol 0, I)$）。

​ 在反向 SDE 中，红色的项 ${\color{red} \nabla_{\boldsymbol x} \log p_t(\boldsymbol x)}$ 正是我们在 score-based models 中定义的 score function，记为 $\boldsymbol s(\boldsymbol x, t)$。与早期 score-based models 不同的是，这里的 score function 明确地依赖于时间 $t$（或者说，依赖于噪声水平）。实际上，在早期的 score-based models 中，$p(\boldsymbol x)$ 指的是在特定噪声水平扰动下的数据分布，因此它也隐式地依赖于扰动（或时间）。SDE 将这种依赖性明确化为 $p_t(\boldsymbol x)$

​ 离散形式下，前向和反向过程可以近似为：

$$\begin{aligned} \text{前向: } \quad \boldsymbol x_{k+1} &\approx \boldsymbol x_k + f(\boldsymbol x_k, t_k)\Delta t + g(t_k)\sqrt{\Delta t}\boldsymbol z_k \\ \text{反向: } \quad \boldsymbol x_{k-1} &\approx \boldsymbol x_k + \left[ f(\boldsymbol x_k, t_k) - g^2(t_k) {\color{red} \nabla_{\boldsymbol x} \log p_{t_k}(\boldsymbol x_k)} \right](-\Delta t') + g(t_k)\sqrt{\Delta t'}\boldsymbol z'_k \\ &\approx \boldsymbol x_k - \left[ f(\boldsymbol x_k, t_k) - g^2(t_k) {\color{red} \boldsymbol s(\boldsymbol x_k, t_k)} \right]\Delta t' + g(t_k)\sqrt{\Delta t'}\boldsymbol z'_k \end{aligned}$$

（注意：这里 $\Delta t$ 和 $\Delta t'$ 均为正的时间步长，反向过程是从 $t_k$ 到 $t_{k-1} = t_k - \Delta t'$）。

​ 如果我们希望从随机噪声（先验分布 $p_T$）中采样生成真实数据（目标分布 $p_0$），我们只需要模拟这个反向 SDE。注意到，漂移项 $f(\boldsymbol x,t)$ 和扩散项 $g(t)$ 在前向过程中是人为设定的，因此是已知的。所以，求解反向过程的关键在于估计 score function $\nabla_{\boldsymbol x} \log p_t(\boldsymbol x)$。这正是 SDE 生成模型的训练核心：训练一个神经网络 $\boldsymbol s_\theta(\boldsymbol x, t)$ 来逼近真实的 score function。

​ 因此，对于 SDE 模型，我们可以采用类似 score matching 的方法来训练模型 $\boldsymbol s_\theta(\boldsymbol x, t)$，其优化目标通常为：

$$J(\theta) = \mathbb{E}_{t \sim \mathcal{U}(0,T)} \mathbb{E}_{\boldsymbol x_0 \sim p_0(\boldsymbol x)} \mathbb{E}_{\boldsymbol x_t \sim p_t(\boldsymbol x|\boldsymbol x_0)} \left[ \lambda(t) \Vert \boldsymbol s_\theta(\boldsymbol x_t, t) - \nabla_{\boldsymbol x_t} \log p_t(\boldsymbol x_t|\boldsymbol x_0) \Vert^2_2 \right]$$

其中 $\lambda(t)$ 是一个与时间相关的正权重函数，$\nabla_{\boldsymbol x_t} \log p_t(\boldsymbol x_t|\boldsymbol x_0)$ 是给定 $\boldsymbol x_0$ 时 $\boldsymbol x_t$ 的真实 score。

SDE 与 DDPM

​ 通过上述介绍，我们不难发现基于 SDE 的 score-based model 与 DDPM (Denoising Diffusion Probabilistic Models) 之间存在诸多相似之处。下面我们将展示 DDPM 实际上可以被视为一种特定 SDE 的离散化实现。

DDPM 的前向 SDE (VP SDE)

​ 在 DDPM 中，前向加噪过程被定义为一系列离散步骤：

$$\boldsymbol{x}_k=\sqrt{1-\beta_k}\boldsymbol{x}_{k-1}+\sqrt{\beta_k}\boldsymbol\epsilon_{k-1},\quad\boldsymbol\epsilon_{k-1}\sim\mathcal{N}(\boldsymbol 0,I)$$

其中 $k \in \{1, \dots, N\}$，$N$ 是总的扩散步数，$\beta_k$ 是预设的噪声方差表。为了将其与连续时间的 SDE 联系起来，我们将时间 $t$ 标准化到 $[0, T]$（通常 $T=1$）。离散时间步 $k$ 对应连续时间 $t = k/N \cdot T$。设 $\Delta t = T/N$。我们可以将 $\beta_k$ 重新参数化为与连续时间相关的函数 $\beta(t)$，使得 $\beta_k \approx \beta(t_k) \Delta t$ （这里假设 $\Delta t = 1/N$，是为了计算简便表述）。

​ 考虑 $\boldsymbol x(t)$ 和 $\boldsymbol x(t+\Delta t)$ 的关系：

$$\boldsymbol{x}(t+\Delta t) = \sqrt{1-\beta(t+\Delta t)\Delta t}\boldsymbol{x}(t)+\sqrt{\beta(t+\Delta t)\Delta t}\boldsymbol\epsilon(t) \\ \approx \left(1 - \frac{1}{2}\beta(t+\Delta t)\Delta t\right)\boldsymbol{x}(t) + \sqrt{\beta(t+\Delta t)\Delta t}\boldsymbol\epsilon(t)$$

整理后得到：

$$\boldsymbol{x}(t+\Delta t) - \boldsymbol{x}(t) \approx -\frac{1}{2}\beta(t+\Delta t)\Delta t \boldsymbol{x}(t) + \sqrt{\beta(t+\Delta t)\Delta t}\boldsymbol\epsilon(t)$$

当 $\Delta t \to 0$，并且假设 $\beta(t+\Delta t) \to \beta(t)$，上式可以写作 SDE 的形式：

$$d\boldsymbol x_t = -\frac{1}{2}\beta(t)\boldsymbol x_t dt + \sqrt{\beta(t)} d\boldsymbol w_t$$

这就是所谓的方差保持（Variance Preserving, VP）SDE。在此 SDE 中：

$$f(\boldsymbol x_t, t) = -\frac{1}{2}\beta(t)\boldsymbol x_t, \quad g(t) = \sqrt{\beta(t)}$$

DDPM 的逆向 SDE

​ 根据前向 SDE 和通用的反向 SDE 公式，DDPM 对应的反向 SDE 为：

$$\begin{aligned} d\boldsymbol x_t &= \left[ f(\boldsymbol x_t, t) - g^2(t) \nabla_{\boldsymbol x_t} \log p_t(\boldsymbol x_t) \right] dt + g(t) d\overline{\boldsymbol w}_t \\ &= \left[ -\frac{1}{2}\beta(t)\boldsymbol x_t - \beta(t) \nabla_{\boldsymbol x_t} \log p_t(\boldsymbol x_t) \right] dt + \sqrt{\beta(t)} d\overline{\boldsymbol w}_t \end{aligned}$$

​ 在 DDPM 中，score function $\nabla_{\boldsymbol x_t} \log p_t(\boldsymbol x_t)$ 通常通过一个神经网络 $\boldsymbol s_\theta(\boldsymbol x_t, t)$ 来估计。这个网络实际上被训练来预测噪声 $\boldsymbol \epsilon_t$ (给定 $\boldsymbol x_t$ 和 $\boldsymbol x_0$)，两者之间存在如下关系：

$$\boldsymbol x_t = \sqrt{\bar{\alpha}_t}\boldsymbol x_0 + \sqrt{1-\bar{\alpha}_t}\boldsymbol \epsilon$$

其中 $\bar{\alpha}_t = \prod_{s=1}^{k} (1-\beta_s)$。真实的 score function $\nabla_{\boldsymbol x_t} \log p_t(\boldsymbol x_t|\boldsymbol x_0)$ 为：

$$\nabla_{\boldsymbol x_t} \log p_t(\boldsymbol x_t|\boldsymbol x_0) = -\frac{\boldsymbol x_t - \boldsymbol x_0 e^{-\frac{1}{2}\int_0^t \beta(s)ds}}{1 - e^{-\int_0^t \beta(s)ds}} = -\frac{\boldsymbol \epsilon_t}{\sqrt{1 - e^{-\int_0^t \beta(s)ds}}}$$

（这里 $\boldsymbol \epsilon_t$ 是使得 $\boldsymbol x_t = \boldsymbol x_0 e^{-\frac{1}{2}\int_0^t \beta(s)ds} + \sqrt{1 - e^{-\int_0^t \beta(s)ds}} \boldsymbol \epsilon_t$ 成立的标准高斯噪声）。
DDPM 训练的噪声预测模型 $\boldsymbol \epsilon_\theta(\boldsymbol x_t, t)$ 与 score 模型 $\boldsymbol s_\theta(\boldsymbol x_t, t)$ 的关系为：

$$\boldsymbol s_\theta(\boldsymbol x_t, t) = -\frac{\boldsymbol \epsilon_\theta(\boldsymbol x_t, t)}{\sqrt{1 - \bar{\alpha}_t}}$$

其中 $\bar{\alpha}_t$ 是与 DDPM 中 $\alpha_k$ 累乘对应的连续时间量。

​ DDPM 的祖先采样（ancestral sampling）过程可以被视为上述逆向 SDE 的一种特定离散化求解器。例如，Euler-Maruyama 方法对逆向 SDE 进行离散化（时间步从 $t$ 到 $t-\Delta t$，即 $dt = -\Delta t$）：

$$\begin{aligned} \boldsymbol x_{t-\Delta t} \approx& \boldsymbol x_t + \left[ -\frac{1}{2}\beta(t)\boldsymbol x_t - \beta(t) \boldsymbol s_\theta(\boldsymbol x_t, t) \right] (-\Delta t) + \sqrt{\beta(t)} \sqrt{\Delta t} \boldsymbol z_t \\ =& \boldsymbol x_t + \left[ \frac{1}{2}\beta(t)\boldsymbol x_t + \beta(t) \boldsymbol s_\theta(\boldsymbol x_t, t) \right] \Delta t + \sqrt{\beta(t)\Delta t} \boldsymbol z_t \end{aligned}$$

这个形式与 DDPM 论文中推导出的采样步骤是紧密相关的，尽管 DDPM 的采样器有其特定的形式和推导

​ 为了更清晰地展示这种联系，我们首先写出经过替换 $\boldsymbol s_\theta(\boldsymbol x_t, t) = -\frac{\boldsymbol \epsilon_\theta(\boldsymbol x_t, t)}{\sqrt{1 - \bar{\alpha}_t}}$ 后的 Euler-Maruyama 离散形式。记 $\Delta\beta_t = \beta(t)\Delta t$ 为单步离散的噪声方差：

$$\boldsymbol x_{t-\Delta t} \approx \left(1 + \frac{1}{2}\Delta\beta_t\right) \boldsymbol x_t - \frac{\Delta\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol \epsilon_\theta(\boldsymbol x_t, t) + \sqrt{\Delta\beta_t} \boldsymbol z_t \quad (\text{SDE Euler-Maruyama})$$

DDPM 论文中祖先采样步骤（若取采样方差为 $\beta_t^{\text{DDPM}}$，对应此处的 $\Delta\beta_t$）可以写作：

$$\boldsymbol x_{t-\Delta t} = \frac{1}{\sqrt{1-\Delta\beta_t}} \boldsymbol x_t - \frac{\Delta\beta_t}{\sqrt{1-\Delta\beta_t}\sqrt{1-\bar{\alpha}_t}} \boldsymbol \epsilon_\theta(\boldsymbol x_t, t) + \sqrt{\Delta\beta_t} \boldsymbol z_t \quad (\text{DDPM Sampler})$$

比较两式：

1. 噪声项 $\sqrt{\Delta\beta_t} \boldsymbol z_t$ 完全相同
2. $\boldsymbol x_t$ 的系数：在 DDPM Sampler 中为 $(1-\Delta\beta_t)^{-1/2}$，其泰勒展开为 $1 + \frac{1}{2}\Delta\beta_t + \frac{3}{8}(\Delta\beta_t)^2 + \dots$。SDE Euler-Maruyama 中的系数 $1 + \frac{1}{2}\Delta\beta_t$ 是其一阶近似
3. $\boldsymbol \epsilon_\theta(\boldsymbol x_t, t)$ 的系数：在 DDPM Sampler 中为 $-\frac{\Delta\beta_t}{\sqrt{1-\bar{\alpha}_t}}(1-\Delta\beta_t)^{-1/2}$。展开后为 $-\frac{\Delta\beta_t}{\sqrt{1-\bar{\alpha}_t}}(1 + \frac{1}{2}\Delta\beta_t + \dots) = -\frac{\Delta\beta_t}{\sqrt{1-\bar{\alpha}_t}} - \frac{1}{2}\frac{(\Delta\beta_t)^2}{\sqrt{1-\bar{\alpha}_t}} + \dots$。SDE Euler-Maruyama 中的系数 $-\frac{\Delta\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$ 是其主导项

因此，当 $\Delta\beta_t$（即 $\beta(t)\Delta t$）很小时，Euler-Maruyama 离散化与 DDPM 的采样步骤非常接近。DDPM 的采样器可以看作是对应逆向过程的一个更精确的（针对其离散推导的）数值解法

​ 推导到这里可以发现，DDPM 的核心机制，无论是前向加噪还是逆向去噪，都可以被统一在 SDE 的框架下进行描述和理解。这为我们提供了一个更普适的视角来看待和设计扩散模型，并允许我们利用 SDE 理论中的各种数值求解器进行采样

SDE 与 SMLD (NCSN)

​ 除了 DDPM，另一类 score-based 生成模型是基于朗之万动力学（Langevin Dynamics）的 Score Matching with Langevin Dynamics (SMLD)，也常被称为 Noise Conditional Score Networks (NCSN)。SMLD 同样可以被 SDE 框架所统一

SMLD 的前向 SDE (VE SDE)

​ SMLD/NCSN 的核心思想是在一系列递增的噪声水平 $\{\sigma_1 < \sigma_2 < \dots < \sigma_M\}$ 下扰动数据，并为每个噪声水平训练一个 score network $\boldsymbol s_\theta(\boldsymbol x, \sigma_i) \approx \nabla_{\boldsymbol x} \log p_{\sigma_i}(\boldsymbol x)$。
​ 这个过程可以用一个连续时间的 SDE 来描述，通常被称为方差爆炸（Variance Exploding, VE）SDE。VE SDE 的一般形式为：

$$d\boldsymbol x_t = g(t) d\boldsymbol w_t$$

​ 注意到，这个 SDE 的漂移项 $f(\boldsymbol x_t, t) = \boldsymbol 0$。扩散系数 $g(t)$ 的选择需要使得在时间 $t$ 时，$\boldsymbol x_t$ 的条件分布 $p_t(\boldsymbol x_t | \boldsymbol x_0)$ 的方差与 SMLD 中离散噪声水平 $\sigma(t)^2$ 相匹配。具体来说，从 $\boldsymbol x_0$ 出发，经过时间 $t$ 后，$\boldsymbol x_t$ 的分布为：

$$p_t(\boldsymbol x_t | \boldsymbol x_0) = \mathcal{N}(\boldsymbol x_t; \boldsymbol x_0, \int_0^t g(s)^2 ds \cdot I)$$

​ 我们希望 $\int_0^t g(s)^2 ds = \sigma(t)^2$，其中 $\sigma(t)$ 是一个随时间 $t$（从 $0$ 到 $T$）单调递增的函数，例如从 $\sigma_{\text{min}}$ (接近0) 变化到 $\sigma_{\text{max}}$。对上式两边关于 $t$ 求导，可得：

$$g(t)^2 = \frac{d}{dt} \sigma(t)^2$$

​ 因此，$g(t) = \sqrt{\frac{d}{dt} \sigma(t)^2}$。一个常见的 $\sigma(t)$ 选择是指数形式，例如 $\sigma(t) = \sigma_{\text{min}} \left(\frac{\sigma_{\text{max}}}{\sigma_{\text{min}}}\right)^{t/T}$，这使得噪声方差随时间指数增长

SMLD 的逆向 SDE

​ 知道了 SMLD 对应的前向 SDE（漂移项 $f(\boldsymbol x_t, t) = \boldsymbol 0$，扩散项 $g(t) = \sqrt{\frac{d}{dt} \sigma(t)^2}$），我们可以利用通用的反向 SDE 公式得到其逆向 SDE：

$$\begin{aligned} d\boldsymbol x_t &= \left[ f(\boldsymbol x_t, t) - g^2(t) \nabla_{\boldsymbol x_t} \log p_t(\boldsymbol x_t) \right] dt + g(t) d\overline{\boldsymbol w}_t \\ &= \left[ \boldsymbol 0 - g^2(t) \boldsymbol s_\theta(\boldsymbol x_t, t) \right] dt + g(t) d\overline{\boldsymbol w}_t \\ &= -g^2(t) \boldsymbol s_\theta(\boldsymbol x_t, t) dt + g(t) d\overline{\boldsymbol w}_t \end{aligned}$$

​ 其中 $\boldsymbol s_\theta(\boldsymbol x_t, t)$ 是神经网络对真实 score $\nabla_{\boldsymbol x_t} \log p_t(\boldsymbol x_t)$ 的估计。在 SMLD 的实践中，这个网络通常以噪声水平 $\sigma(t)$ 作为条件输入，即 $\boldsymbol s_\theta(\boldsymbol x_t, \sigma(t))$。

与退火朗之万动力学的联系

​ SMLD/NCSN 在生成样本时采用的是退火朗之万动力学（Annealed Langevin Dynamics）。该过程从一个高噪声水平 $\sigma_M$ 开始，逐步降低噪声水平到 $\sigma_1$，在每个噪声水平 $\sigma_i$ 下，通过多步朗之万采样来精炼样本：

$$\boldsymbol x^{(k+1)} = \boldsymbol x^{(k)} + \eta_i \boldsymbol s_\theta(\boldsymbol x^{(k)}, \sigma_i) + \sqrt{2\eta_i} \boldsymbol z_k$$

其中 $\eta_i$ 是步长，$\boldsymbol z_k \sim \mathcal{N}(\boldsymbol 0, I)$。

​ 我们可以看到，上述朗之万动力学步骤与逆向 SDE 的 Euler-Maruyama 离散化形式非常相似。对 SMLD 的逆向 SDE 进行离散化（时间步从 $t$ 到 $t-\Delta t$，即 $dt = -\Delta t$）：

$$\begin{aligned} \boldsymbol x_{t-\Delta t} \approx& \boldsymbol x_t + \left[-g^2(t) \boldsymbol s_\theta(\boldsymbol x_t, t)\right](-\Delta t) + g(t)\sqrt{\Delta t} \boldsymbol z_t \\ =& \boldsymbol x_t + g^2(t) \boldsymbol s_\theta(\boldsymbol x_t, t) \Delta t + g(t)\sqrt{\Delta t} \boldsymbol z_t \end{aligned}$$

​ 如果我们将朗之万动力学中的步长 $\eta_i$ 对应于 $g^2(t)\Delta t / 2$ （或者说，如果 $g^2(t)\Delta t = \alpha_i$ 且 $g(t)\sqrt{\Delta t} = \sqrt{2\alpha_i}$，则需要 $g^2(t)\Delta t = 2\alpha_i$），那么两者形式上就非常接近了。更准确地说，朗之万动力学本身就是对某个目标概率分布 $p(\boldsymbol x)$ 进行采样的随机过程，其对应的 SDE（过阻尼朗之万方程）为 $d\boldsymbol X_t = \nabla \log p(\boldsymbol X_t) dt + \sqrt{2} d\boldsymbol W_t$（这里步长被吸收到时间尺度中）。
​ SMLD 的逆向 SDE $d\boldsymbol x_t = -g^2(t) \boldsymbol s_\theta(\boldsymbol x_t, t) dt + g(t) d\overline{\boldsymbol w}_t$ 正是指导样本从噪声向数据演化的过程。退火朗之万动力学可以被视为求解这个逆向 SDE 的一种特定数值方法，其中 score $\boldsymbol s_\theta(\boldsymbol x_t, t)$ 扮演了 $\nabla \log p_t(\boldsymbol x_t)$ 的角色，而 $g(t)$ 控制了噪声的注入。

SMLD 的训练目标

​ SMLD 的训练目标是让神经网络 $\boldsymbol s_\theta(\boldsymbol x, \sigma_i)$ 在每个离散的噪声水平 $\sigma_i$ 上逼近真实的 score $\nabla_{\boldsymbol x} \log p(\boldsymbol x | \boldsymbol x_0, \sigma_i)$。对于高斯扰动核 $p(\boldsymbol x | \boldsymbol x_0, \sigma_i) = \mathcal{N}(\boldsymbol x; \boldsymbol x_0, \sigma_i^2 I)$，真实的 score 是：

$$\nabla_{\boldsymbol x} \log p(\boldsymbol x | \boldsymbol x_0, \sigma_i) = - \frac{\boldsymbol x - \boldsymbol x_0}{\sigma_i^2}$$

​ SMLD 的损失函数通常是所有噪声水平上带权重的 score matching 损失之和：

$$J_{\text{SMLD}}(\theta) = \sum_{i=1}^M \lambda(\sigma_i) \mathbb{E}_{p_0(\boldsymbol x_0)} \mathbb{E}_{\boldsymbol x \sim p(\boldsymbol x|\boldsymbol x_0, \sigma_i)} \left[ \Vert \boldsymbol s_\theta(\boldsymbol x, \sigma_i) - \nabla_{\boldsymbol x} \log p(\boldsymbol x|\boldsymbol x_0, \sigma_i) \Vert^2_2 \right]$$

​ 这与 SDE 的通用训练目标形式一致，其中 $\lambda(\sigma_i)$ 是权重，通常取 $\sigma_i^2$ 或者 $g(\text{map to continuous time}(\sigma_i))^2$。SDE 框架将离散的噪声水平 $\sigma_i$ 推广到了连续的时间 $t$ 和连续的噪声尺度函数 $\sigma(t)$。

​ 通过 SDE 的视角，SMLD/NCSN 模型也被纳入了统一的框架中，其前向过程是一个无漂移的 SDE，逆向过程则通过估计随时间（或噪声水平）变化的 score function 来驱动。这不仅加深了我们对这些模型的理解，也为开发新的采样算法和模型变体提供了理论基础