基于分数的生成模型 (Score-based Generative Models)

基于分数的生成模型（Score-based Generative Model）

Overview

​ 首先，我们来探讨一下什么是基于分数的生成模型（Score-based Generative Models，简称SGM）。其核心思想可以概括为：该模型通过估计数据概率密度函数的对数梯度（即“分数”），并借鉴**朗之万动力学（Langevin Dynamics）**的原理来逐步生成新的数据样本

Score Matching (分数匹配)

​ 假设我们有一组从真实数据分布 $p_{\text{data}}(\boldsymbol x)$ 中采样得到的数据点 $\{\boldsymbol x_1, \boldsymbol x_2, \dots, \boldsymbol x_n\}$。我们的目标是学习一个模型 $p_\theta(\boldsymbol x)$ 来拟合真实数据分布，这通常通过最大化对数似然来实现：

$$\max_\theta \sum_{i=1}^n \log p_\theta(\boldsymbol x_i)$$

​ 为了处理概率分布的归一化约束（积分为1且非负），我们通常将概率密度函数参数化为能量模型的形式：

$$p_\theta(\boldsymbol x) = \frac{e^{-f_\theta(\boldsymbol x)}}{\int_\mathcal{X} e^{-f_\theta(\boldsymbol y)}d\boldsymbol y}$$

​ 其中 $f_\theta(\boldsymbol x)$ 是一个能量函数（通常由神经网络表示），而 $Z_\theta = \int_\mathcal{X} e^{-f_\theta(\boldsymbol y)}d\boldsymbol y$ 是归一化常数，也称为配分函数（partition function）。此时，对数似然函数可以表示为：

$$\log p_\theta(\boldsymbol x)= -f_\theta(\boldsymbol x) - \log Z_\theta$$

​ 因此，最大化对数似然的优化问题转变为：

$$\max_\theta \left( - \sum_{i=1}^n f_\theta(\boldsymbol x_i) - n \log Z_\theta \right)$$

​ 然而，直接计算配分函数 $Z_\theta$ (及其梯度) 通常是难以处理的（intractable），因为它涉及到对整个数据空间的高维积分。这使得直接优化上述目标函数变得非常困难。例如，在变分自编码器（VAE）中，通过引入证据下界（ELBO）来规避这个问题。本文将介绍另一种基于分数匹配（Score Matching）的方法来解决这一挑战。

Score (分数) 的定义：

​ 我们将数据点 $\boldsymbol x$ 处的分数（score）定义为对数概率密度函数 $\log p_\theta(\boldsymbol x)$ 关于输入数据 $\boldsymbol x$ 的梯度：

$$s_\theta(\boldsymbol x) = \nabla_x \log p_\theta(\boldsymbol x)$$

​ 结合能量模型的形式，由于 $Z_\theta$ 不依赖于 $\boldsymbol x$，我们有：

$$s_\theta(\boldsymbol x) = \nabla_x (-f_\theta(\boldsymbol x) - \log Z_\theta) = -\nabla_x f_\theta(\boldsymbol x)$$

​ 分数匹配的核心思想是训练一个模型 $s_\theta(\boldsymbol x)$ 来直接逼近真实数据分布 $p_{\text{data}}(\boldsymbol x)$ 的分数函数 $s_{\text{data}}(\boldsymbol x) = \nabla_x \log p_{\text{data}}(\boldsymbol x)$。其优化目标通常表示为两者之间L2距离的期望：

$$\theta^* = \arg\min_\theta \frac{1}{2} \mathbb{E}_{\boldsymbol x \sim p_{\text{data}}(\boldsymbol x)}\left\Vert s_{\text{data}}(\boldsymbol x) - s_\theta(\boldsymbol x) \right\Vert^2$$

​ 其中 $s_{\text{data}}(\boldsymbol x)$ 是真实数据分布的分数函数。直接计算 $s_{\text{data}}(\boldsymbol x)$ 是不可行的，因为它需要知道 $p_{\text{data}}(\boldsymbol x)$。幸运的是，可以通过一些技巧（如显式分数匹配、去噪分数匹配或切片分数匹配）来规避这个问题，使得我们只需要从 $p_{\text{data}}(\boldsymbol x)$ 中采样即可。

​ 一种避免直接计算 $s_{\text{data}}(\boldsymbol x)$ 的方法是显式分数匹配 (Explicit Score Matching)。假设 $p_{\text{data}}(\boldsymbol x)$ 在数据空间的边界处趋于零，通过分部积分法，上述优化目标可以等价地转化为（忽略不依赖 $\theta$ 的常数项）：

$$\theta^* = \arg\min_\theta \mathbb{E}_{\boldsymbol x \sim p_{\text{data}}(\boldsymbol x)}\left[ \frac{1}{2}\Vert s_\theta(\boldsymbol x; \theta) \Vert^2 + \nabla_x \cdot s_\theta(\boldsymbol x; \theta) \right]$$

​ 其中 $\nabla_x \cdot s_\theta(\boldsymbol x; \theta)$ 是 $s_\theta(\boldsymbol x; \theta)$ 的散度 (divergence)。这个形式虽然避免了 $s_{\text{data}}(\boldsymbol x)$，但计算散度的 Hessian 矩阵迹（trace of Hessian）在实践中对于高维数据和复杂模型（如神经网络）仍然可能计算量巨大。

​ 正如其名，“分数”即指数据点 $\boldsymbol x$ 处对数概率密度 $\log p(\boldsymbol x)$ 关于 $\boldsymbol x$ 的梯度 $\nabla_x \log p(\boldsymbol x)$。这个概念也被称为 Stein Score。基于分数的模型的核心任务就是训练一个网络（通常称为分数网络 $s_\theta(\boldsymbol x)$）来准确地估计这个分数。

物理意义

​ 分数的物理意义非常直观：它指向数据点 $\boldsymbol x$ 处概率密度函数值增长最快的方向。换言之，沿着分数的方向移动，可以使得样本的对数似然（即概率密度）增加。一旦我们训练好了一个分数网络 $s_\theta(\boldsymbol x) \approx \nabla_x \log p_{\text{data}}(\boldsymbol x)$，理论上我们可以从任意初始点出发，通过梯度上升法（因为分数是梯度的方向）来迭代更新样本，使其逐渐靠近高概率密度区域，从而生成符合数据分布的样本。

然而，单纯的梯度上升可能会导致生成的样本仅仅是训练数据的简单复制，缺乏多样性。为了生成新颖且多样化的样本，同时确保它们仍然符合目标数据分布，引入了随机性。朗之万动力学（Langevin Dynamics）采样方法便为此提供了一个有效的框架。

Langevin Dynamics (朗之万动力学)

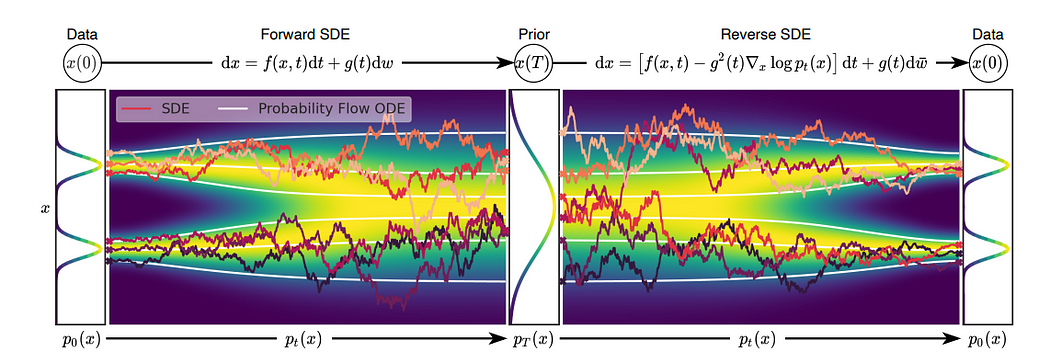
​ 朗之万动力学最初用于描述物理学中粒子在势场中的随机运动（如布朗运动）。在生成模型领域，它被借鉴为一种从复杂分布中采样的方法。其核心思想是：从一个简单的先验分布（如高斯分布）中随机初始化一个样本，然后通过迭代更新使其逐渐向目标数据分布的高概率密度区域移动。这个更新过程不仅包括了沿着分数（梯度）方向的确定性移动，还引入了高斯噪声以保证生成样本的多样性和随机性。其随机微分方程 (SDE) 形式可以写作：

$$d \boldsymbol X(t) = -\nabla_x U(\boldsymbol X(t)) dt + \sqrt{2D} d\boldsymbol W(t)$$

​ 其中 $U(\boldsymbol X(t))$ 是势能函数（在我们的场景下，可以理解为与 $-\log p(\boldsymbol X(t))$ 相关），$\nabla_x U(\boldsymbol X(t))$ 是其梯度，$D$ 是扩散系数（控制噪声强度），$d\boldsymbol W(t)$ 是维纳过程（表示高斯白噪声）。

​ 将其离散化，令时间步长为 $\epsilon = dt$，并设 $U(\boldsymbol x) = f_\theta(\boldsymbol x)$（回忆 $s_\theta(\boldsymbol x) = -\nabla_x f_\theta(\boldsymbol x)$），则更新规则为：

$$\boldsymbol x_{t+\epsilon} = \boldsymbol x_t + s_\theta(\boldsymbol x_t)\epsilon + \sqrt{2D\epsilon}\boldsymbol z_t$$

其中 $\boldsymbol z_t \sim \mathcal{N}(0, I)$ 是标准高斯噪声。这个更新规则可以看作是在能量函数的负梯度方向（即向能量低处，概率高处移动）进行一步，同时加入一个高斯噪声项。

我们从一个简单的先验分布（如标准正态分布 $\mathcal{N}(\boldsymbol 0, \boldsymbol I)$）采样初始点 $\boldsymbol x_0$，通过多次迭代上述步骤，期望最终得到的样本 $\boldsymbol x_T$ 近似服从目标数据分布 $p_{\text{data}}(\boldsymbol x)$。

朗之万动力学有一个重要的性质：如果其对应的 Fokker-Planck 方程的稳态解为 $p_\theta(\boldsymbol x) \propto \exp(-f_\theta(\boldsymbol x))$（这对应于吉布斯分布中有效温度为1的情况），那么扩散系数 $D$ 通常设为1。此时，采样过程可以表示为：

$$\boldsymbol x_{t+\epsilon} = \boldsymbol x_t + s_\theta(\boldsymbol x_t)\epsilon + \sqrt{2\epsilon} \boldsymbol z_t$$

通过迭代这个更新规则足够多次，从 $\boldsymbol x_0 \sim \mathcal{N}(\boldsymbol 0, \boldsymbol I)$ 开始，最终得到的样本 $\boldsymbol x_T$ 将近似服从模型分布 $p_\theta(\boldsymbol x)$。

Denoising Score Matching (去噪分数匹配)

Noise Conditional Score Network (NCSN, 噪声条件分数网络)

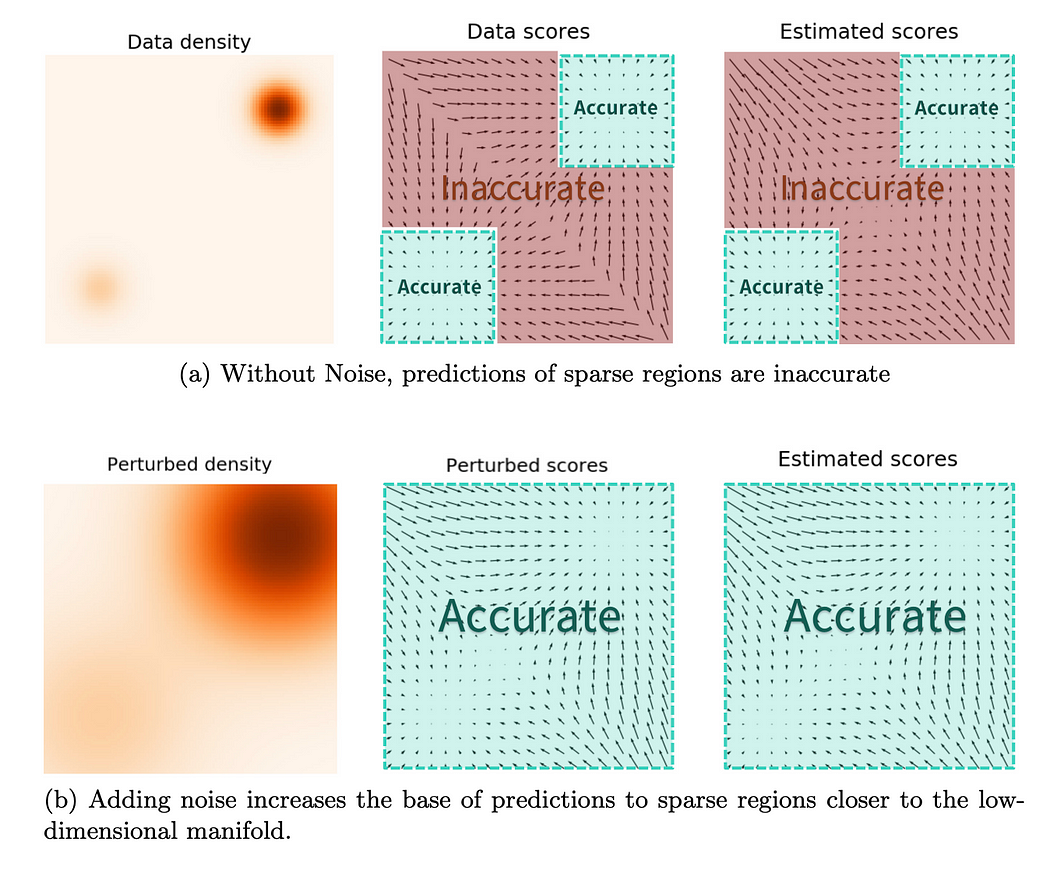
原始的分数匹配方法（尤其是显式分数匹配）在处理高维数据（如图像）时面临挑战。根据流形假设（manifold hypothesis），真实数据往往分布在高维空间中的一个低维流形上。这意味着在流形之外的区域，数据密度 $p_{\text{data}}(\boldsymbol x)$ 趋近于零，导致分数 $\nabla_x \log p_{\text{data}}(\boldsymbol x)$ 未定义或难以估计。然而，在通过朗之万动力学等方法生成样本时，采样路径可能会穿过这些低密度区域。如果模型在这些区域的分数估计不准确，生成过程就会不稳定。

为了解决这个问题，一个关键的改进是引入噪声扰动数据。去噪分数匹配（Denoising Score Matching, DSM）通过向原始数据 $\boldsymbol x'$ (来自 $p_{\text{data}}$) 添加不同强度的高斯噪声 $\boldsymbol n \sim \mathcal{N}(\boldsymbol 0, \sigma^2 \boldsymbol I)$ 来生成扰动后的数据 $\boldsymbol x = \boldsymbol x' + \boldsymbol n$。扰动后的数据分布 $q_\sigma(\boldsymbol x) = \int p_{\text{data}}(\boldsymbol x') \mathcal{N}(\boldsymbol x | \boldsymbol x', \sigma^2 \boldsymbol I) d\boldsymbol x'$ 会覆盖更广阔的空间，尤其是在原始数据的低密度区域。

此时，我们不再直接估计 $p_{\text{data}}(\boldsymbol x)$ 的分数，而是估计扰动后数据分布 $q_\sigma(\boldsymbol x)$ 的分数 $\nabla_x \log q_\sigma(\boldsymbol x)$。更进一步地，可以训练一个条件分数网络 $s_\theta(\boldsymbol x, \sigma)$ 来估计给定噪声水平 $\sigma$ 时，条件概率 $q_\sigma(\boldsymbol x | \boldsymbol x')$ 的对数梯度，即 $\nabla_x \log q_\sigma(\boldsymbol x | \boldsymbol x')$。这种模型被称为噪声条件分数网络（Noise Conditional Score Network, NCSN）。

优化目标推导

对于给定的原始数据点 $\boldsymbol x'$ 和噪声水平 $\sigma$，扰动过程定义为 $\boldsymbol x \sim q_\sigma(\boldsymbol x|\boldsymbol x') = \mathcal{N}(\boldsymbol x | \boldsymbol x', \sigma^2 \boldsymbol I)$。这个条件高斯分布的对数似然关于 $\boldsymbol x$ 的梯度（即条件分数）可以解析地计算出来：

$$\log q_\sigma(\boldsymbol x|\boldsymbol x') = -\frac{\|\boldsymbol x - \boldsymbol x'\|^2}{2\sigma^2} + \text{const}$$

$$\nabla_x \log q_\sigma(\boldsymbol x|\boldsymbol x') = -\frac{\boldsymbol x - \boldsymbol x'}{\sigma^2}$$

去噪分数匹配的目标是训练一个噪声条件分数网络 $s_\theta(\boldsymbol x, \sigma)$ 来逼近这个真实的条件分数 $\nabla_x \log q_\sigma(\boldsymbol x|\boldsymbol x')$。损失函数定义为两者均方误差的期望，期望取自真实数据分布 $p_{\text{data}}(\boldsymbol x')$ 和噪声条件分布 $q_\sigma(\boldsymbol x|\boldsymbol x')$：

$$\begin{aligned} J(\theta; \sigma) &= \frac{1}{2} \mathbb{E}_{\boldsymbol x' \sim p_{\text{data}}(\boldsymbol x')} \mathbb{E}_{\boldsymbol x \sim q_\sigma(\boldsymbol x|\boldsymbol x')} \left\| s_\theta(\boldsymbol x, \sigma) - \nabla_x \log q_\sigma(\boldsymbol x|\boldsymbol x') \right\|^2 \\ &= \frac{1}{2} \mathbb{E}_{\boldsymbol x' \sim p_{\text{data}}(\boldsymbol x')} \mathbb{E}_{\boldsymbol x \sim \mathcal{N}(\boldsymbol x | \boldsymbol x', \sigma^2 \boldsymbol I)} \left\| s_\theta(\boldsymbol x, \sigma) + \frac{\boldsymbol x - \boldsymbol x'}{\sigma^2} \right\|^2 \end{aligned}$$

这个目标函数的好处在于，真实的条件分数 $\nabla_x \log q_\sigma(\boldsymbol x|\boldsymbol x')$ 是已知的，因此可以直接用于监督学习。通过训练模型来预测 $-\frac{\boldsymbol x - \boldsymbol x'}{\sigma^2}$（即预测噪声 $\boldsymbol n = \boldsymbol x - \boldsymbol x'$ 的一个缩放版本），模型就学会了在给定扰动数据 $\boldsymbol x$ 和噪声水平 $\sigma$ 的情况下，如何“去噪”并指向原始数据 $\boldsymbol x'$ 的方向。

多噪声尺度训练：

单一噪声水平 $\sigma$ 可能无法兼顾所有情况。较大的 $\sigma$ 有助于填充低密度区域，但可能过度模糊原始数据结构，导致分数估计不准确；较小的 $\sigma$ 能更好地保留数据细节，但对低密度区域的覆盖不足。为了解决这个问题，NCSN 采用多尺度噪声训练策略。即选择一系列递减的噪声水平 $\{\sigma_1 > \sigma_2 > \dots > \sigma_L\}$，其中 $\sigma_1$ 足够大以覆盖数据空间，$\sigma_L$ 足够小以接近原始数据分布。

模型 $s_\theta(\boldsymbol x, \sigma_i)$ 针对每个噪声水平进行训练，总的损失函数是各个噪声水平下损失的加权平均：

$$\mathcal{L}(\theta; \{\sigma_i\}_{i=1}^L) = \frac{1}{L} \sum_{i=1}^L \lambda(\sigma_i) J(\theta; \sigma_i)$$

权重因子 $\lambda(\sigma_i)$ 用于平衡不同噪声水平的贡献。一个常见的选择是 $\lambda(\sigma_i) = \sigma_i^2$，这有助于抵消损失项中 $\frac{1}{\sigma^2}$ 的影响，使得不同噪声尺度下的梯度贡献更加均衡。

核心代码分析

Loss损失函数：

def anneal_dsm_score_estimation(scorenet, samples, labels, sigmas, anneal_power=2.):
    # labels: 批次中每个样本对应的噪声等级索引 (0 to L-1)
    # sigmas: 预定义的噪声标准差序列 [sigma_1, sigma_2, ..., sigma_L]
    # used_sigmas: 根据 labels 从 sigmas 中选取的、当前批次各样本对应的噪声标准差
    # 维度从 (batch_size,) 扩展到 (batch_size, 1, 1, 1) 以匹配图像维度 (samples.shape)
    used_sigmas = sigmas[labels].view(samples.shape[0], *([1] * len(samples.shape[1:])))
    
    # perturbed_samples (x_perturbed) = samples (x_clean) + noise
    # noise = used_sigmas * torch.randn_like(samples)
    perturbed_samples = samples + torch.randn_like(samples) * used_sigmas
    
    # target_score = ∇_x_perturbed log q(x_perturbed | x_clean)
    #            = - (x_perturbed - x_clean) / sigma^2
    #            = - noise / sigma^2 
    # (perturbed_samples - samples) is the actual noise added
    target = - 1 / (used_sigmas ** 2) * (perturbed_samples - samples)
    
    # 模型预测的 score
    scores = scorenet(perturbed_samples, labels) # labels (i.e., sigma_idx) is passed to scorenet
    
    target = target.view(target.shape[0], -1) # Flatten to (batch_size, num_features)
    scores = scores.view(scores.shape[0], -1) # Flatten to (batch_size, num_features)

    # loss_per_sample = 0.5 * ||scores - target_score||^2_2 * lambda(sigma)
    # lambda(sigma) = sigma^anneal_power (通常 anneal_power=2, 即 lambda(sigma) = sigma^2)
    # .sum(dim=-1) 计算L2范数的平方 (按元素平方后求和)
    # .squeeze() 移除 used_sigmas 的多余维度 (1,1,1)
    loss = 1 / 2. * ((scores - target) ** 2).sum(dim=-1) * used_sigmas.squeeze() ** anneal_power

    return loss.mean(dim=0) # Average loss over the batch

Annealed Langevin Dynamics (退火朗之万动力学) 采样：

这部分代码实现了退火朗之万动力学采样算法，即在不同噪声水平下逐步进行朗之万采样，噪声水平逐渐降低。

def anneal_Langevin_dynamics(self, x_mod, scorenet, sigmas, n_steps_each=100, step_lr=0.00002):
    images = []

    with torch.no_grad():
        # 按照预设的噪声标准差序列 sigmas (从大到小) 进行退火朗之万动力学采样
        for c, sigma in tqdm.tqdm(enumerate(sigmas), total=len(sigmas), desc='annealed Langevin dynamics sampling'):
            # labels: 当前噪声等级的索引 (c)，用于输入到 scorenet
            labels = torch.ones(x_mod.shape[0], device=x_mod.device) * c
            labels = labels.long()

            # step_size (epsilon_i in some notations) for Langevin update at current noise level sigma_i
            # step_lr * (sigma / sigmas[-1])^2 is a common heuristic for step size schedule
            # (epsilon_i / epsilon_L) = (sigma_i / sigma_L)^2
            # This implies larger step sizes for larger sigmas (earlier stages)
            step_size = step_lr * (sigma / sigmas[-1]) ** 2
            
            # 在当前噪声水平 sigma 下，执行 n_steps_each 次朗之万更新
            for s in range(n_steps_each):
                images.append(torch.clamp(x_mod, 0.0, 1.0).to('cpu')) # Store intermediate or final image
                
                # Langevin update: x_t+1 = x_t + (step_size/2) * grad_x log p(x_t) + sqrt(step_size) * z_t
                # Or, more commonly: x_t+1 = x_t + step_size * grad_x log p(x_t) + sqrt(2 * step_size) * z_t
                # The code uses: x_mod = x_mod + step_size * grad + noise
                # where noise = torch.randn_like(x_mod) * np.sqrt(step_size * 2)
                # This matches the second form if 'step_size' here is the epsilon in that formula.
                
                # noise_term = sqrt(2 * step_size) * z_t (z_t ~ N(0,I))
                noise = torch.randn_like(x_mod) * np.sqrt(step_size * 2)
                # 网络估计的分数 grad = s_theta(x_mod, labels)
                grad = scorenet(x_mod, labels)
                # 朗之万动力学更新方程
                x_mod = x_mod + step_size * grad + noise

        # Add the final image after all steps
        images.append(torch.clamp(x_mod, 0.0, 1.0).to('cpu'))
        return images