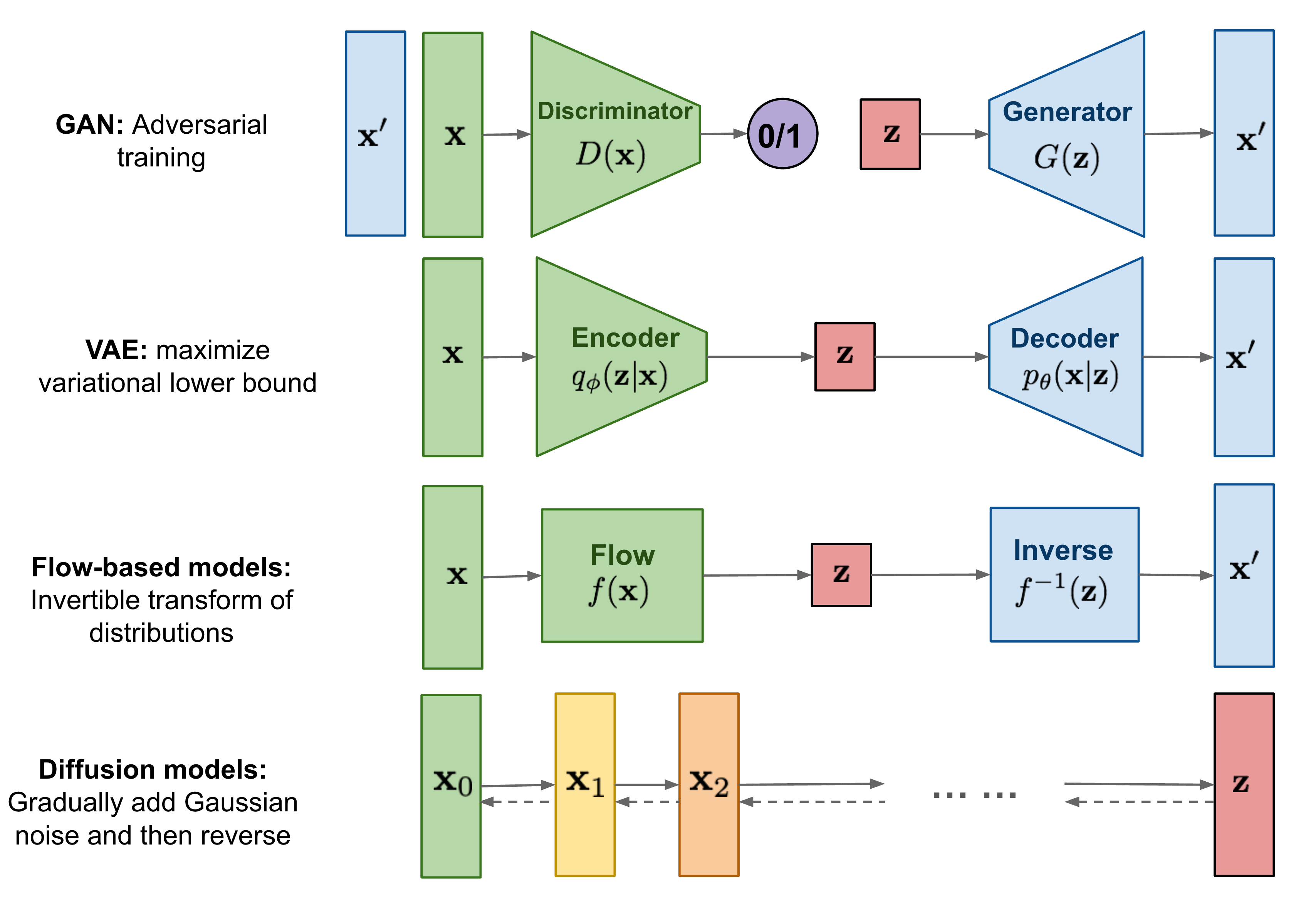
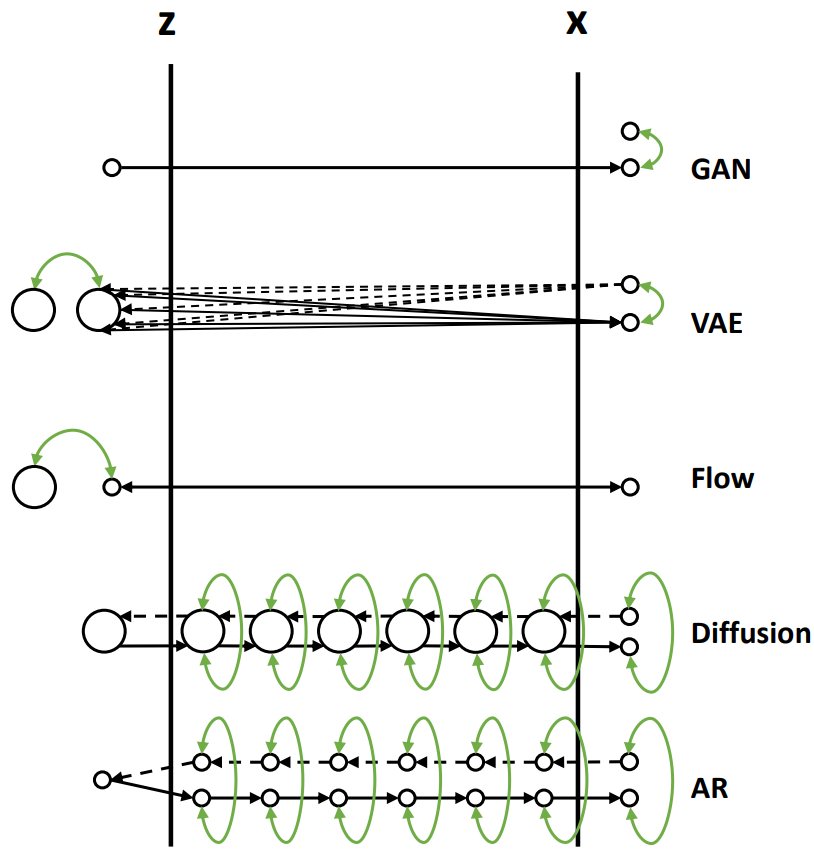
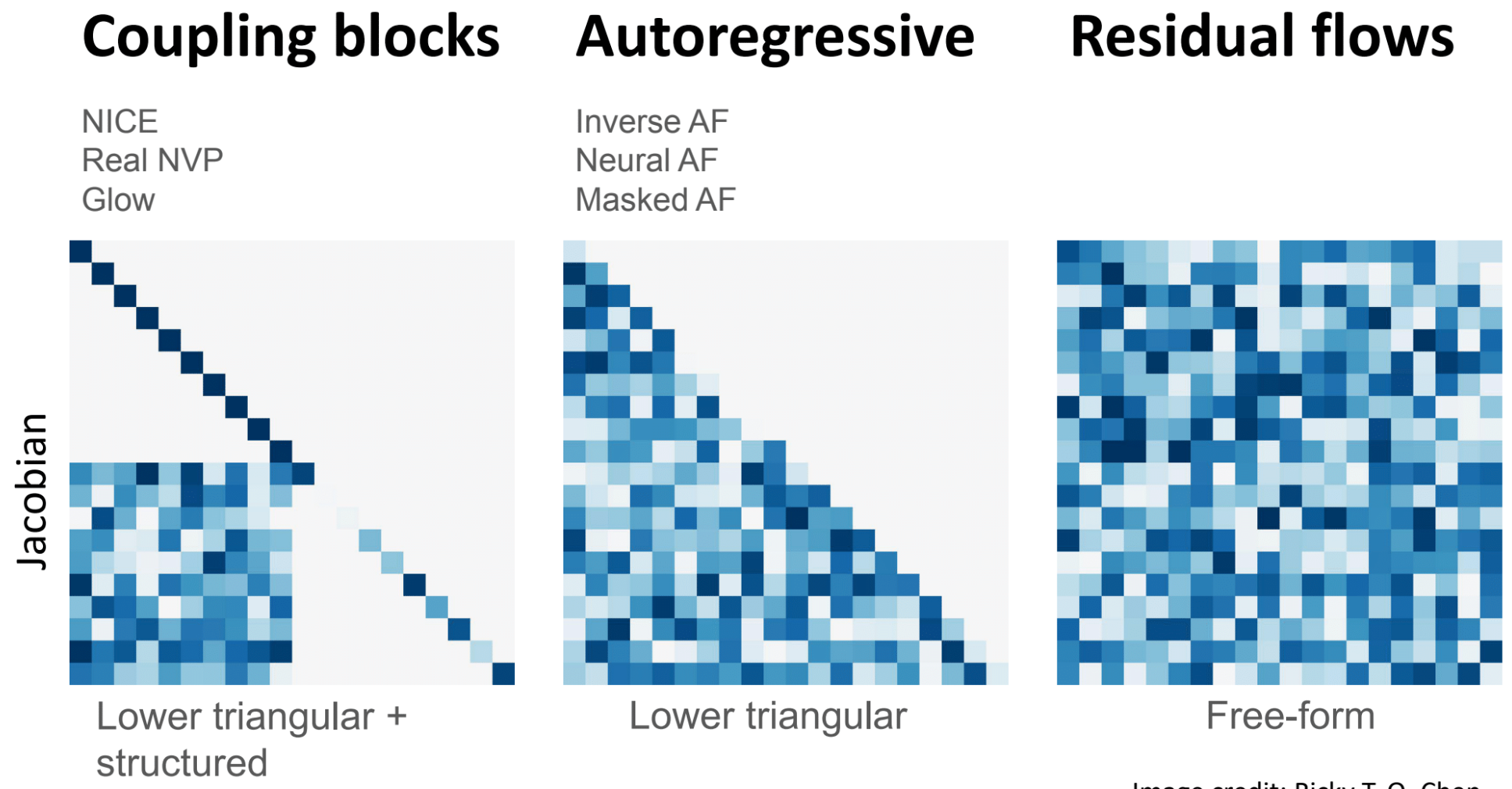
在探索模型结构的多样性时,主流的生成模型大致可分为几类:GAN (生成对抗网络)、VAE (变分自编码器)、Flow (流模型)、Diffusion (扩散模型)以及 AR (自回归模型)等。它们各有特点,致力于从不同角度解决数据生成的问题。
首先需要回顾一下生成模型的核心目标:最大化观测数据的对数似然 。简单来说,我们希望模型学习到的数据分布 p θ ( x ) p_\theta(\boldsymbol x) p θ ( x ) p d a t a ( x ) p_{data}(\boldsymbol x) p d a t a ( x )
然而,直接对高维复杂数据的对数似然 log p θ ( x ) \log p_\theta(\boldsymbol x) log p θ ( x )
基于流 (Flow-based) 的模型则提供了一条直接优化对数似然的路径。 其核心思想在于构建一个从真实数据分布到某个简单、易于处理的先验分布(例如标准正态分布)的可逆映射 (双射)。借助数学中的变量替换定理 (Change of Variables Theorem) ,这个可逆映射可以将复杂数据分布下的概率密度计算,转换为在简单先验分布下的概率密度计算
具体来说,我们的优化目标是最大化训练数据集 { x 1 , x 2 , … , x m } \{\boldsymbol x_1,\boldsymbol x_2,\ldots,\boldsymbol x_m \} { x 1 , x 2 , … , x m } p d a t a p_{data} p d a t a
J ( θ ) = max θ ∑ i = 1 m log p θ ( x i ) J(\theta)=\max_\theta\sum_{i=1}^m \log p_\theta(\boldsymbol x^i)
J ( θ ) = θ max i = 1 ∑ m log p θ ( x i )
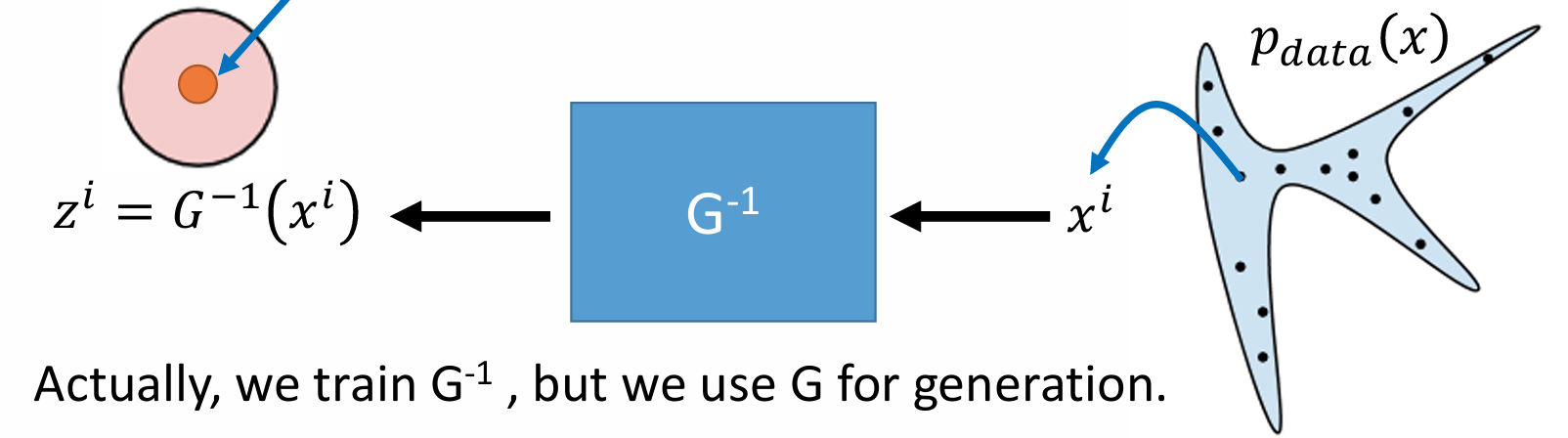
现在,我们引入隐变量 z \boldsymbol z z π ( z ) \pi(\boldsymbol z) π ( z ) N ( 0 , I ) \mathcal{N}(\boldsymbol 0, \boldsymbol I) N ( 0 , I ) G θ : Z → X G_\theta: \mathcal{Z} \to \mathcal{X} G θ : Z → X z \boldsymbol z z x = G θ ( z ) \boldsymbol x = G_\theta(\boldsymbol z) x = G θ ( z ) G θ − 1 : X → Z G_\theta^{-1}: \mathcal{X} \to \mathcal{Z} G θ − 1 : X → Z z = G θ − 1 ( x ) \boldsymbol z = G_\theta^{-1}(\boldsymbol x) z = G θ − 1 ( x )
根据变量替换定理,由 G θ G_\theta G θ p θ ( x ) p_\theta(\boldsymbol x) p θ ( x ) π ( z ) \pi(\boldsymbol z) π ( z )
p θ ( x ) = π ( G θ − 1 ( x ) ) ⋅ ∣ det ( ∂ G θ − 1 ( x ) ∂ x ) ∣ p_\theta(\boldsymbol x) = \pi(G_\theta^{-1}(\boldsymbol x)) \cdot \left| \det \left( \frac{\partial G_\theta^{-1}(\boldsymbol x)}{\partial \boldsymbol x} \right) \right|
p θ ( x ) = π ( G θ − 1 ( x ) ) ⋅ ∣ ∣ ∣ ∣ ∣ det ( ∂ x ∂ G θ − 1 ( x ) ) ∣ ∣ ∣ ∣ ∣
其中,∂ G θ − 1 ( x ) ∂ x \frac{\partial G_\theta^{-1}(\boldsymbol x)}{\partial \boldsymbol x} ∂ x ∂ G θ − 1 ( x ) G θ − 1 G_\theta^{-1} G θ − 1 x \boldsymbol x x ∣ det ( … ) ∣ \left| \det \left( \dots \right) \right| ∣ det ( … ) ∣ ∣ det J G θ − 1 ( x ) ∣ \left| \det J_{G_\theta^{-1}}(\boldsymbol x) \right| ∣ ∣ ∣ ∣ det J G θ − 1 ( x ) ∣ ∣ ∣ ∣ log p θ ( x ) \log p_\theta(\boldsymbol x) log p θ ( x )
log p θ ( x ) = log π ( G θ − 1 ( x ) ) + log ∣ det J G θ − 1 ( x ) ∣ \log p_\theta(\boldsymbol x) = \log \pi(G_\theta^{-1}(\boldsymbol x)) + \log \left| \det J_{G_\theta^{-1}}(\boldsymbol x) \right|
log p θ ( x ) = log π ( G θ − 1 ( x ) ) + log ∣ ∣ ∣ ∣ det J G θ − 1 ( x ) ∣ ∣ ∣ ∣
将此表达式代入我们最初的优化目标 J ( θ ) J(\theta) J ( θ )
J ( θ ) = max θ ∑ i = 1 m [ log π ( G θ − 1 ( x i ) ) + log ∣ det J G θ − 1 ( x i ) ∣ ] J(\theta) = \max_\theta \sum_{i=1}^m \left[ \log \pi(G_\theta^{-1}(\boldsymbol x^i)) + \log \left| \det J_{G_\theta^{-1}}(\boldsymbol x^i) \right| \right]
J ( θ ) = θ max i = 1 ∑ m [ log π ( G θ − 1 ( x i ) ) + log ∣ ∣ ∣ ∣ det J G θ − 1 ( x i ) ∣ ∣ ∣ ∣ ]
这个公式是流模型训练的核心。它由两部分组成:第一项 log π ( G θ − 1 ( x i ) ) \log \pi(G_\theta^{-1}(\boldsymbol x^i)) log π ( G θ − 1 ( x i ) ) x i \boldsymbol x^i x i π \pi π log ∣ det J G θ − 1 ( x i ) ∣ \log \left| \det J_{G_\theta^{-1}}(\boldsymbol x^i) \right| log ∣ ∣ ∣ ∣ det J G θ − 1 ( x i ) ∣ ∣ ∣ ∣
流模型成功的关键在于精心设计的可逆变换函数 f : X → Z f:\mathcal{X}\to \mathcal{Z} f : X → Z G θ − 1 G_\theta^{-1} G θ − 1
log p X ( x ) = log p Z ( f ( x ) ) + log ∣ det J f ( x ) ∣ \log p_{\mathcal{X}}(\boldsymbol x) = \log p_{\mathcal{Z}}(f(\boldsymbol x)) + \log\left|\det J_f(\boldsymbol x)\right|
log p X ( x ) = log p Z ( f ( x ) ) + log ∣ det J f ( x ) ∣
这里有几个关键点需要强调:
维度保持特性:与 VAE 等模型可能将数据压缩到低维隐空间不同,流模型中的可逆变换通常要求输入 X \mathcal{X} X Z \mathcal{Z} Z
参数共享的映射:Flow 模型的核心是学习一个可逆映射 f θ : X ↔ Z f_\theta: \mathcal{X} \leftrightarrow \mathcal{Z} f θ : X ↔ Z X \mathcal{X} X Z \mathcal{Z} Z f θ f_\theta f θ G θ − 1 G_\theta^{-1} G θ − 1 Z \mathcal{Z} Z X \mathcal{X} X f θ − 1 f_\theta^{-1} f θ − 1 G θ G_\theta G θ θ \theta θ
一个重要的观察是:在流模型中,隐空间 Z \mathcal{Z} Z X \mathcal{X} X 如果我们随意设计一般的可逆变换 f k f_k f k det J f k \det J_{f_k} det J f k O ( D 3 ) \mathcal{O}(D^3) O ( D 3 ) D D D
因此,对变换 f k f_k f k
必须可逆 :这是流模型的根本。雅可比行列式易于计算 :这是模型实用性的保证。通常希望计算复杂度为 O ( D ) \mathcal{O}(D) O ( D )
模型
前向过程
反向过程
Normalizing Flow
通过显式的可学习变换将样本分布变换为标准高斯分布
从标准高斯分布采样,并通过上述变换的逆变换得到生成的样本
Diffusion Model
通过不可学习的 schedule 对样本进行加噪,多次加噪变换为标准高斯分布
从标准高斯分布采样,通过模型隐式地学习反向过程的噪声,去噪得到生成样本
“归一化流”这一名称强调了模型将复杂数据分布“归一化”为一个标准、简单的目标分布(通常是标准正态分布)的过程。这与 VAE 中强制后验分布逼近标准正态先验有相似之处
G G G
x → f 1 z 1 → f 2 z 2 → … z K − 1 → f K z K = z \boldsymbol x \xrightarrow{f_1} \boldsymbol z_1 \xrightarrow{f_2} \boldsymbol z_2 \xrightarrow{\dots} \boldsymbol z_{K-1} \xrightarrow{f_K} \boldsymbol z_K = \boldsymbol z
x f 1 z 1 f 2 z 2 … z K − 1 f K z K = z
其中 x \boldsymbol x x z \boldsymbol z z f k f_k f k
对于这样的复合变换,根据链式法则,总的雅可比行列式是对每一层雅可比行列式的连乘。因此,总的对数似然贡献也是各层对数雅可比行列式之和:
log p X ( x ) = log p Z ( z ) + ∑ k = 1 K log ∣ det J f k ( z k − 1 ) ∣ \log p_{\mathcal{X}}(\boldsymbol x) = \log p_{\mathcal{Z}}(\boldsymbol z) + \sum_{k=1}^K \log \left| \det J_{f_k}(\boldsymbol z_{k-1}) \right|
log p X ( x ) = log p Z ( z ) + k = 1 ∑ K log ∣ det J f k ( z k − 1 ) ∣
其中 z 0 = x \boldsymbol z_0 = \boldsymbol x z 0 = x z k = f k ( z k − 1 ) \boldsymbol z_k = f_k(\boldsymbol z_{k-1}) z k = f k ( z k − 1 )
此时,优化目标变为:
J ( θ ) = max θ ∑ i = 1 m [ log π ( z i ) + ∑ k = 1 K log ∣ det J f k ( z k − 1 i ) ∣ ] J(\theta) = \max_\theta \sum_{i=1}^m \left[ \log \pi(\boldsymbol z^i) + \sum_{k=1}^K \log \left| \det J_{f_k}(\boldsymbol z_{k-1}^i) \right| \right]
J ( θ ) = θ max i = 1 ∑ m [ log π ( z i ) + k = 1 ∑ K log ∣ ∣ ∣ det J f k ( z k − 1 i ) ∣ ∣ ∣ ]
其中 z i \boldsymbol z^i z i x i \boldsymbol x^i x i
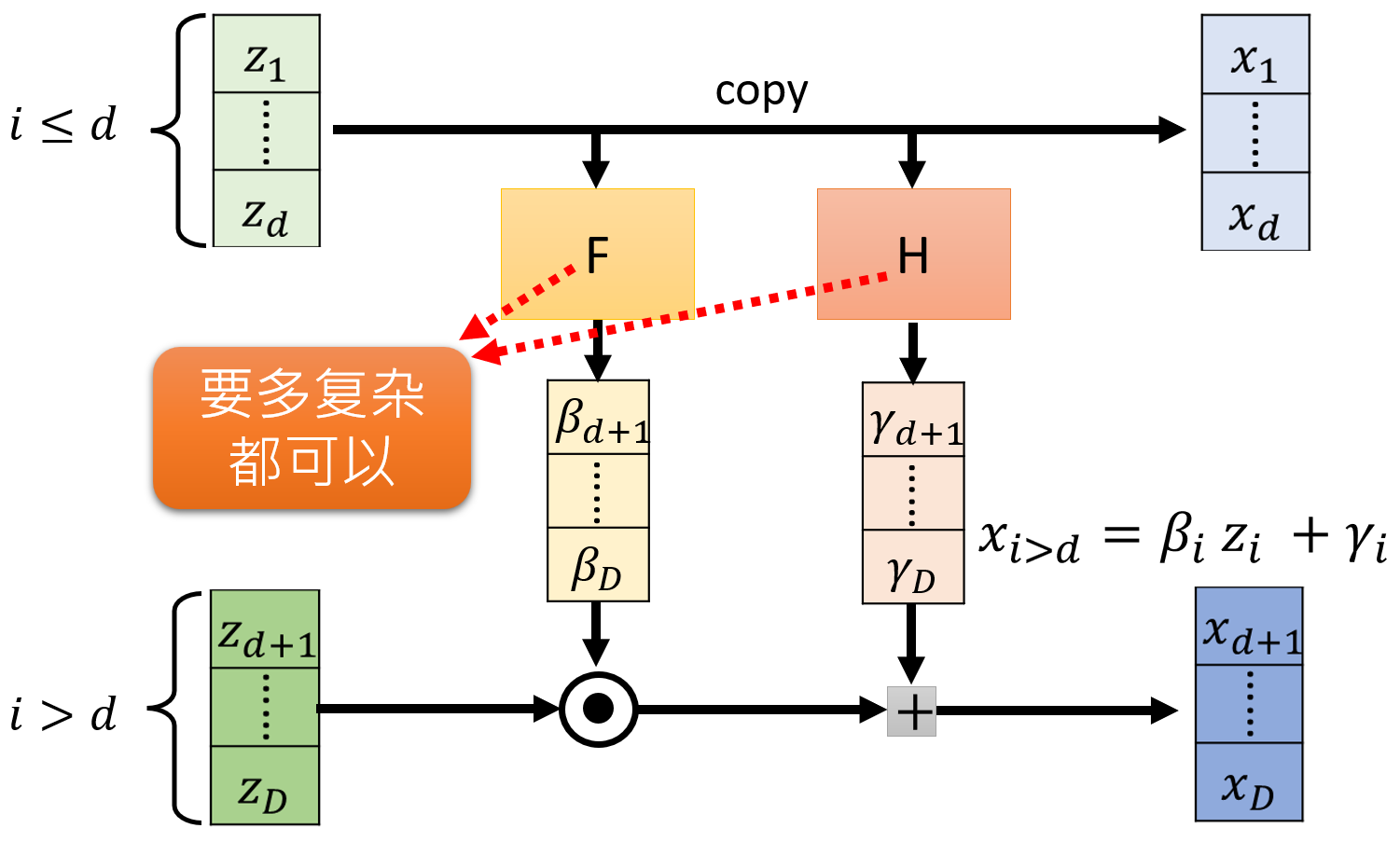
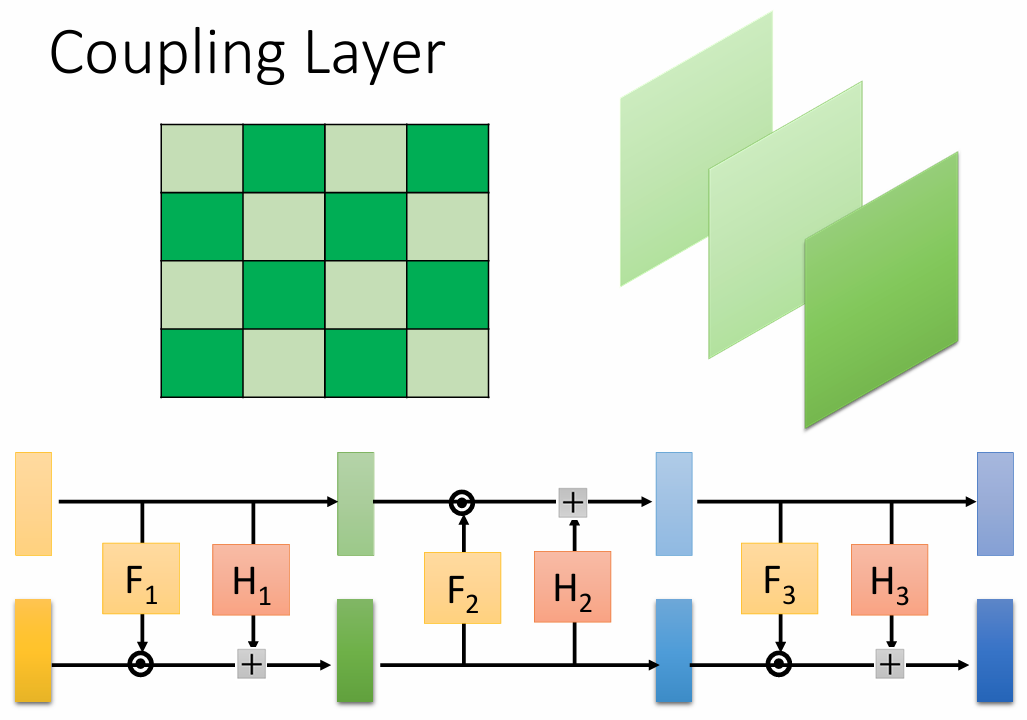
为了满足 flow 模型可逆且雅可比矩阵便于计算的要求,有多种巧妙的层设计,其中仿射耦合层 是 RealNVP、NICE 和 Glow 等模型的核心组件。
其基本思想是将输入向量 x \boldsymbol x x x = ( x A , x B ) \boldsymbol x = (\boldsymbol x_A, \boldsymbol x_B) x = ( x A , x B ) x A \boldsymbol x_A x A x B \boldsymbol x_B x B s s s t t t x A \boldsymbol x_A x A
具体地,对于一个从 x \boldsymbol x x y \boldsymbol y y G G G
将输入 x \boldsymbol x x x A , x B \boldsymbol x_A, \boldsymbol x_B x A , x B
第一部分保持不变:y A = x A \boldsymbol y_A = \boldsymbol x_A y A = x A
第二部分经过仿射变换:y B = x B ⊙ exp ( s ( x A ) ) + t ( x A ) \boldsymbol y_B = \boldsymbol x_B \odot \exp(s(\boldsymbol x_A)) + t(\boldsymbol x_A) y B = x B ⊙ exp ( s ( x A ) ) + t ( x A ) ⊙ \odot ⊙ s s s t t t x A \boldsymbol x_A x A exp ( s ( x A ) ) \exp(s(\boldsymbol x_A)) exp ( s ( x A ) )
这个变换的雅可比矩阵 J G ( x ) J_G(\boldsymbol x) J G ( x ) x A \boldsymbol x_A x A d d d x B \boldsymbol x_B x B D − d D-d D − d
J f ( x ) = [ I d 0 d × ( D − d ) ∂ y B ∂ x A d i a g ( exp ( s ( x A ) ) ) ] \boldsymbol{J}_f(\boldsymbol x) =
\begin{bmatrix}
\mathbb{I}_d & \boldsymbol{0}_{d\times(D-d)} \\
\frac{\partial\boldsymbol{y}_B} {\partial\boldsymbol{x}_A} & \mathrm{diag}(\exp(s(\boldsymbol{x}_A)))
\end{bmatrix}
J f ( x ) = [ I d ∂ x A ∂ y B 0 d × ( D − d ) d i a g ( exp ( s ( x A ) ) ) ]
这是一个下三角矩阵(或上三角,取决于分割和更新的顺序),其行列式就是对角线元素的乘积:
det ( J G ( x ) ) = ∏ j exp ( s j ( x A ) ) = exp ( ∑ j s j ( x A ) ) \det(J_G(\boldsymbol x)) = \prod_j \exp(s_j(\boldsymbol x_A)) = \exp\left(\sum_j s_j(\boldsymbol x_A)\right)
det ( J G ( x ) ) = j ∏ exp ( s j ( x A ) ) = exp ( j ∑ s j ( x A ) )
因此,对数雅可比行列式可以非常高效地计算:
log ∣ det ( J f ( x ) ) ∣ = ∑ j s j ( x A ) \log |\det(J_f(\boldsymbol x))| = \sum_j s_j(\boldsymbol x_A)
log ∣ det ( J f ( x ) ) ∣ = j ∑ s j ( x A )
这个变换的逆变换也容易计算:
x A = y A \boldsymbol x_A = \boldsymbol y_A x A = y A x B = ( y B − t ( y A ) ) ⊙ exp ( − s ( y A ) ) \boldsymbol x_B = (\boldsymbol y_B - t(\boldsymbol y_A)) \odot \exp(-s(\boldsymbol y_A)) x B = ( y B − t ( y A ) ) ⊙ exp ( − s ( y A ) )
为了让所有维度都能得到更新,通常会交替地将不同部分的维度作为 x A \boldsymbol x_A x A
通过堆叠多个这样的耦合层,并可能在它们之间加入维度重排(如1x1卷积或固定置换),模型可以学习到非常复杂和灵活的数据变换。
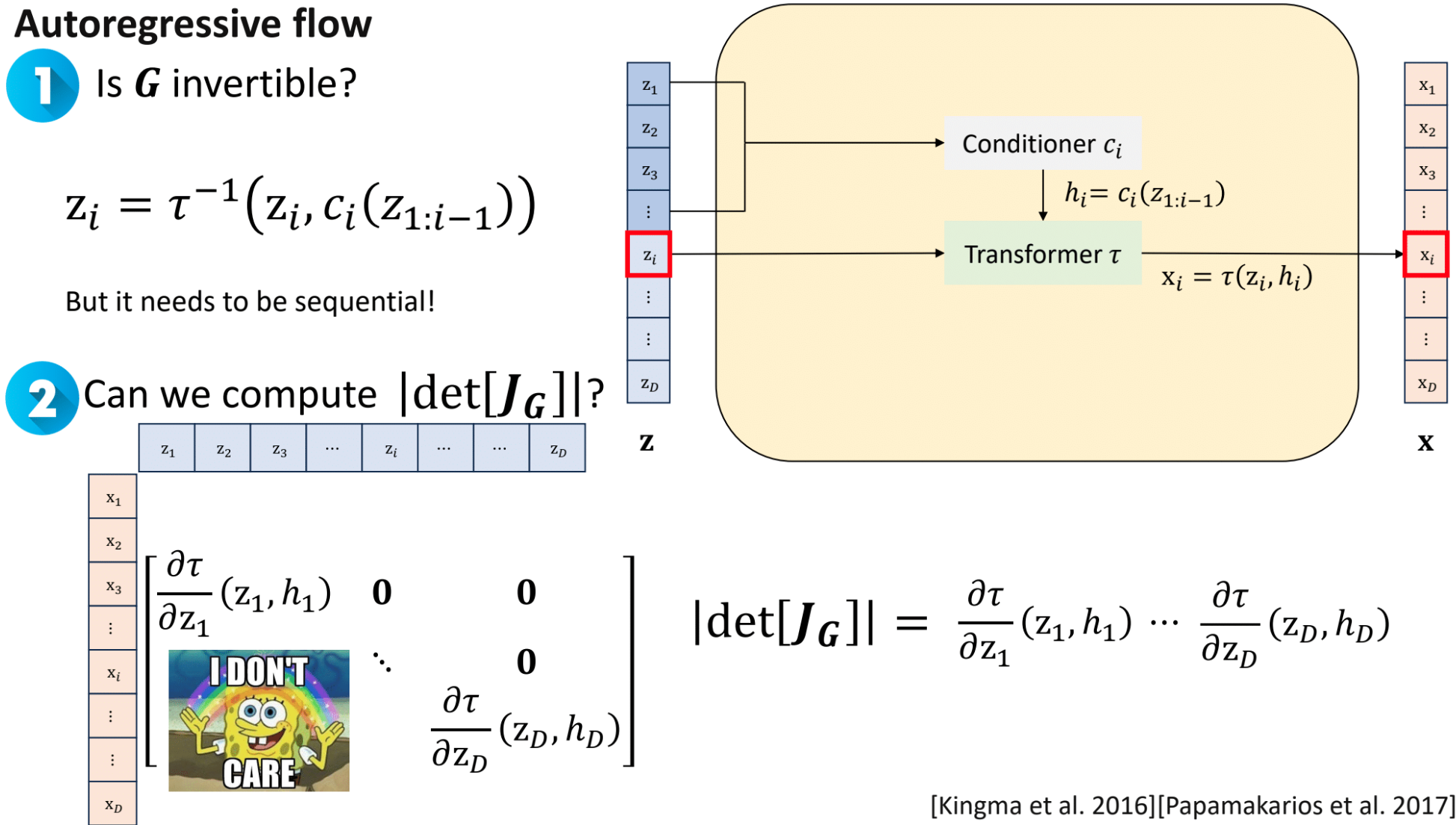
自回归流 (Autoregressive Flow) 是另一类重要的流模型,在自回归流中,数据点 x = ( x 1 , x 2 , … , x D ) \boldsymbol x = (x_1, x_2, \ldots, x_D) x = ( x 1 , x 2 , … , x D ) x i x_i x i z i z_i z i x \boldsymbol x x z \boldsymbol z z i − 1 i-1 i − 1
对于从 z \boldsymbol z z x \boldsymbol x x G G G
x i = τ ( z i ; h i ( z < i ) ) x_i = \tau(z_i; \boldsymbol{h}_i(\boldsymbol z_{<i}))
x i = τ ( z i ; h i ( z < i ) )
其中 τ \tau τ z i z_i z i α i \alpha_i α i β i \beta_i β i h i \boldsymbol{h}_i h i z < i = ( z 1 , … , z i − 1 ) \boldsymbol z_{<i} = (z_1, \ldots, z_{i-1}) z < i = ( z 1 , … , z i − 1 ) x i x_i x i z i z_i z i i i i z 1 , … , z i − 1 z_1, \ldots, z_{i-1} z 1 , … , z i − 1
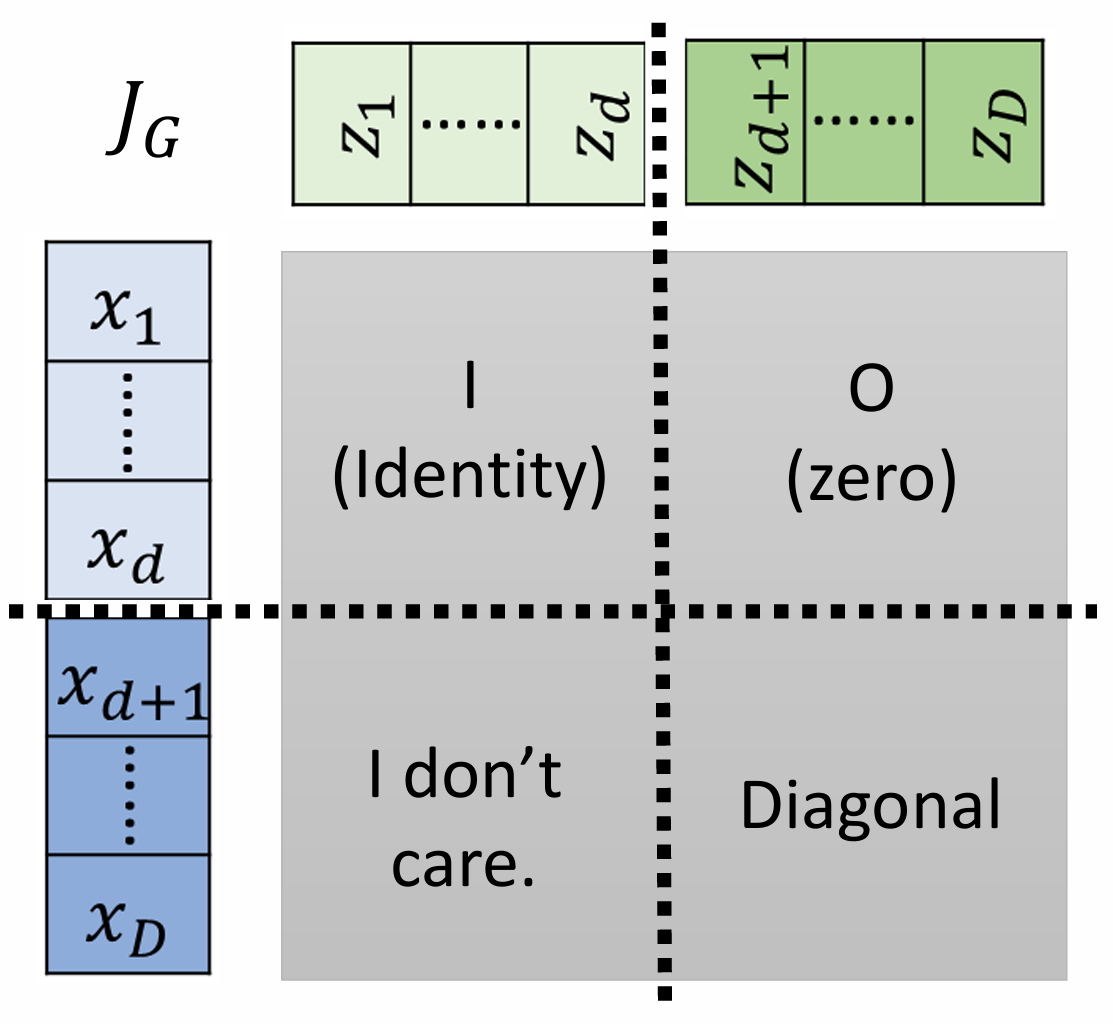
这种结构的关键优势在于其雅可比矩阵的特性。对于上述从 z \boldsymbol z z x \boldsymbol x x G G G J G ( z ) = ∂ x ∂ z J_G(\boldsymbol z) = \frac{\partial \boldsymbol x}{\partial \boldsymbol z} J G ( z ) = ∂ z ∂ x
J f ( z ) = ( ∂ x 1 ∂ z 1 0 ⋯ 0 ∂ x 2 ∂ z 1 ∂ x 2 ∂ z 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ ∂ x D ∂ z 1 ∂ x D ∂ z 2 ⋯ ∂ x D ∂ z D ) J_f(\boldsymbol z) =
\begin{pmatrix}
\frac{\partial x_1}{\partial z_1} & 0 & \cdots & 0 \\
\frac{\partial x_2}{\partial z_1} & \frac{\partial x_2}{\partial z_2} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial x_D}{\partial z_1} & \frac{\partial x_D}{\partial z_2} & \cdots & \frac{\partial x_D}{\partial z_D}
\end{pmatrix}
J f ( z ) = ⎝ ⎜ ⎜ ⎜ ⎜ ⎛ ∂ z 1 ∂ x 1 ∂ z 1 ∂ x 2 ⋮ ∂ z 1 ∂ x D 0 ∂ z 2 ∂ x 2 ⋮ ∂ z 2 ∂ x D ⋯ ⋯ ⋱ ⋯ 0 0 ⋮ ∂ z D ∂ x D ⎠ ⎟ ⎟ ⎟ ⎟ ⎞
这是因为 x i x_i x i z 1 , … , z i z_1, \ldots, z_i z 1 , … , z i z j z_{j} z j j > i j>i j > i ∂ x i ∂ z j = 0 \frac{\partial x_i}{\partial z_j} = 0 ∂ z j ∂ x i = 0 j > i j>i j > i
三角矩阵的行列式就是其对角线元素的乘积:
det ( J G ( z ) ) = ∏ i = 1 D ∂ x i ∂ z i \det(J_G(\boldsymbol z)) = \prod_{i=1}^D \frac{\partial x_i}{\partial z_i}
det ( J G ( z ) ) = i = 1 ∏ D ∂ z i ∂ x i
如果变换 τ \tau τ x i = α i ( z < i ) z i + β i ( z < i ) x_i = \alpha_i(\boldsymbol z_{<i}) z_i + \beta_i(\boldsymbol z_{<i}) x i = α i ( z < i ) z i + β i ( z < i ) α i ( z < i ) \alpha_i(\boldsymbol z_{<i}) α i ( z < i )
log ∣ det ( J f ( z ) ) ∣ = ∑ i = 1 D log ∣ α i ( z < i ) ∣ \log |\det(J_f(\boldsymbol z))| = \sum_{i=1}^D \log |\alpha_i(\boldsymbol z_{<i})|
log ∣ det ( J f ( z ) ) ∣ = i = 1 ∑ D log ∣ α i ( z < i ) ∣
条件网络 h i \boldsymbol{h}_i h i
采样 (生成):从 p ( z ) p(\boldsymbol z) p ( z ) z \boldsymbol z z x \boldsymbol x x z \boldsymbol z z x i x_i x i h i \boldsymbol{h}_i h i z \boldsymbol z z
似然计算 (训练):计算 p ( x ) p(\boldsymbol x) p ( x ) z = f − 1 ( x ) \boldsymbol z = f^{-1}(\boldsymbol x) z = f − 1 ( x ) z i = τ − 1 ( x i ; h i ( z < i ) ) z_i = \tau^{-1}(x_i; \boldsymbol{h}_i(\boldsymbol z_{<i})) z i = τ − 1 ( x i ; h i ( z < i ) ) z i z_i z i z 1 , … , z i − 1 z_1, \ldots, z_{i-1} z 1 , … , z i − 1
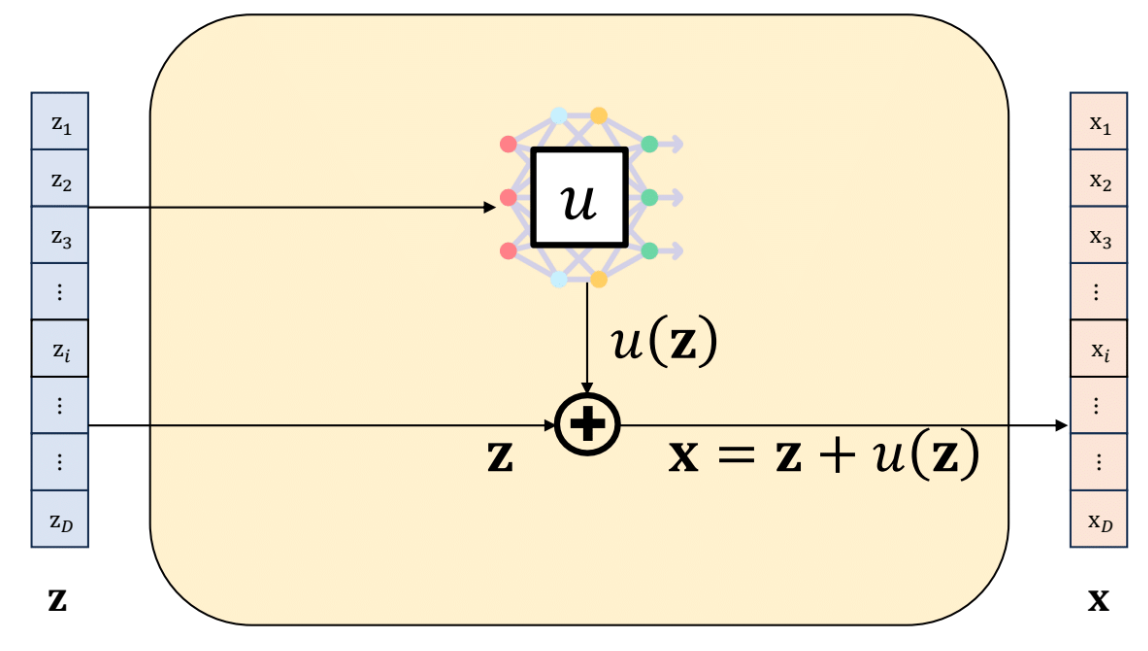
残差流 (Residual Flow, ResFlow) 提供了一种构建可逆变换的替代方法,它借鉴了深度残差网络 (ResNet) 的思想。其核心是将变换 f : X → Y f: \mathcal{X} \to \mathcal{Y} f : X → Y
y = f ( x ) = x + g ( x ; θ ) \boldsymbol y = f(\boldsymbol x) = \boldsymbol x + g(\boldsymbol x; \theta)
y = f ( x ) = x + g ( x ; θ )
其中 g g g θ \theta θ
与耦合层或自回归流不同,上述形式的残差变换通常没有解析的逆函数 f − 1 f^{-1} f − 1 g g g G G G
具体来说,如果 g g g x \boldsymbol x x Lip ( g ) < 1 \text{Lip}(g) < 1 Lip ( g ) < 1 f ( x ) = x + g ( x ) f(\boldsymbol x) = \boldsymbol x + g(\boldsymbol x) f ( x ) = x + g ( x ) x = f − 1 ( y ) \boldsymbol x = f^{-1}(\boldsymbol y) x = f − 1 ( y )
x k + 1 = y − g ( x k ; θ ) \boldsymbol x_{k+1} = \boldsymbol y - g(\boldsymbol x_k; \theta)
x k + 1 = y − g ( x k ; θ )
从某个初始值 x 0 \boldsymbol x_0 x 0 x 0 = y \boldsymbol x_0 = \boldsymbol y x 0 = y x k \boldsymbol x_k x k f − 1 ( y ) f^{-1}(\boldsymbol y) f − 1 ( y ) L i p ( g ) < 1 \mathrm{Lip}(g) < 1 L i p ( g ) < 1 g g g
残差变换的雅可比矩阵为 J G ( x ) = I + J g ( x ) J_G(\boldsymbol x) = \boldsymbol I + J_g(\boldsymbol x) J G ( x ) = I + J g ( x ) J g ( x ) J_g(\boldsymbol x) J g ( x ) g ( x ) g(\boldsymbol x) g ( x ) x \boldsymbol x x det ( I + J g ( x ) ) \det(\boldsymbol I + J_g(\boldsymbol x)) det ( I + J g ( x ) ) O ( D 3 ) \mathcal{O}(D^3) O ( D 3 )
ResFlow 的一个关键贡献是采用了一种无偏的随机估计方法来计算对数雅可比行列式 log ∣ det ( J G ( x ) ) ∣ \log |\det(J_G(\boldsymbol x))| log ∣ det ( J G ( x ) ) ∣
log ∣ det ( I + J g ( x ) ) ∣ = T r ( log ( I + J g ( x ) ) ) \log |\det(\boldsymbol I + J_g(\boldsymbol x))| = \mathrm{Tr}(\log(\boldsymbol I + J_g(\boldsymbol x)))
log ∣ det ( I + J g ( x ) ) ∣ = T r ( log ( I + J g ( x ) ) )
其中 T r ( ⋅ ) \mathrm{Tr}(\cdot) T r ( ⋅ ) log ( I + J g ( x ) ) \log(\boldsymbol I + J_g(\boldsymbol x)) log ( I + J g ( x ) ) J g ( x ) J_g(\boldsymbol x) J g ( x ) L i p ( g ) < 1 \mathrm{Lip}(g)<1 L i p ( g ) < 1
log ( I + A ) = A − A 2 2 + A 3 3 − ⋯ = ∑ k = 1 ∞ ( − 1 ) k + 1 k A k \log(\boldsymbol I + A) = A - \frac{A^2}{2} + \frac{A^3}{3} - \dots = \sum_{k=1}^\infty \frac{(-1)^{k+1}}{k} A^k
log ( I + A ) = A − 2 A 2 + 3 A 3 − ⋯ = k = 1 ∑ ∞ k ( − 1 ) k + 1 A k
然后,Hutchinson迹估计器被用来估计迹:
Hutchinson 迹估计:
对于任意矩阵 M M M T r ( M ) = E v ∼ p ( v ) [ v T M v ] \mathrm{Tr}(M) = \mathbb{E}_{\boldsymbol v \sim p(\boldsymbol v)}[\boldsymbol v^T M \boldsymbol v] T r ( M ) = E v ∼ p ( v ) [ v T M v ] p ( v ) p(\boldsymbol v) p ( v ) { ± 1 } \{\pm 1\} { ± 1 }
因此,对数行列式可以估计为:
log ∣ det ( J f ( x ) ) ∣ ≈ E v ∼ p ( v ) [ v T ( ∑ k = 1 K ( − 1 ) k + 1 k ( J g ( x ) ) k ) v ] \log |\det(J_f(\boldsymbol x))| \approx \mathbb{E}_{\boldsymbol v \sim p(\boldsymbol v)}\left[\boldsymbol v^T \left(\sum_{k=1}^K \frac{(-1)^{k+1}}{k} (J_g(\boldsymbol x))^k\right) \boldsymbol v\right]
log ∣ det ( J f ( x ) ) ∣ ≈ E v ∼ p ( v ) [ v T ( k = 1 ∑ K k ( − 1 ) k + 1 ( J g ( x ) ) k ) v ]
其中 K K K v T ( J g ( x ) ) k v \boldsymbol v^T (J_g(\boldsymbol x))^k \boldsymbol v v T ( J g ( x ) ) k v k k k J g ( x ) J_g(\boldsymbol x) J g ( x ) O ( K ⋅ D ⋅ C g ) \mathcal{O}(K \cdot D \cdot C_g) O ( K ⋅ D ⋅ C g ) C g C_g C g g g g
g g g L i p ( g ) < 1 \mathrm{Lip}(g) < 1 L i p ( g ) < 1 对数雅可比行列式的估计会给损失函数和梯度带来噪声/方差,可能影响训练的稳定性和收敛速度。逆变换依赖迭代求解,可能需要较多计算步骤,尤其是在生成新样本时
流模型的训练遵循严格的极大似然准则。目标是最小化负对数似然 (Negative Log-Likelihood, NLL):
L f l o w = − E x ∼ p d a t a [ log p X ( x ) ] = − E x ∼ p d a t a [ log p Z ( f θ ( x ) ) + ∑ k = 1 K log ∣ det J f k ( z k − 1 ) ∣ ] \mathcal{L}_{\mathrm{flow}} = -\mathbb{E}_{\boldsymbol x \sim p_{\mathrm{data}}}\left[\log p_{\mathcal{X}}(\boldsymbol x)\right] = -\mathbb{E}_{\boldsymbol x \sim p_{\mathrm{data}}}\left[\log p_{\mathcal{Z}}(f_{\theta}(\boldsymbol x)) + \sum_{k=1}^K \log\left|\det J_{f_k}(\boldsymbol z_{k-1})\right|\right]
L f l o w = − E x ∼ p d a t a [ log p X ( x ) ] = − E x ∼ p d a t a [ log p Z ( f θ ( x ) ) + k = 1 ∑ K log ∣ det J f k ( z k − 1 ) ∣ ]
其中 f θ ( x ) f_\theta(\boldsymbol x) f θ ( x ) x \boldsymbol x x z K \boldsymbol z_K z K f k f_k f k k k k J f k J_{f_k} J f k z k − 1 \boldsymbol z_{k-1} z k − 1 k k k
这个损失函数包含两个核心组成部分:
先验匹配项 : log p Z ( f θ ( x ) ) \log p_{\mathcal{Z}}(f_{\theta}(\boldsymbol x)) log p Z ( f θ ( x ) ) f θ ( x ) f_{\theta}(\boldsymbol x) f θ ( x ) p Z p_{\mathcal{Z}} p Z 流形校正项 (体积变化项) : ∑ k = 1 K log ∣ det J f k ( z k − 1 ) ∣ \sum_{k=1}^K \log\left|\det J_{f_k}(\boldsymbol z_{k-1})\right| ∑ k = 1 K log ∣ det J f k ( z k − 1 ) ∣
通过梯度下降等优化算法最小化 L f l o w \mathcal{L}_{\mathrm{flow}} L f l o w f θ f_\theta f θ
训练完成后,我们可以利用学习到的可逆变换进行多种操作:
密度估计 : 对于一个新的数据点 x n e w \boldsymbol x_{new} x n e w f θ ( x n e w ) f_\theta(\boldsymbol x_{new}) f θ ( x n e w ) z n e w \boldsymbol z_{new} z n e w log p X ( x n e w ) = log p Z ( z n e w ) + ∑ log ∣ det J f k ∣ \log p_{\mathcal{X}}(\boldsymbol x_{new}) = \log p_{\mathcal{Z}}(\boldsymbol z_{new}) + \sum \log|\det J_{f_k}| log p X ( x n e w ) = log p Z ( z n e w ) + ∑ log ∣ det J f k ∣ 数据生成 : 要生成新的样本,我们首先从先验分布 p Z p_{\mathcal{Z}} p Z z s a m p l e \boldsymbol z_{sample} z s a m p l e f θ − 1 = f K − 1 ∘ ⋯ ∘ f 1 − 1 f_\theta^{-1} = f_K^{-1} \circ \dots \circ f_1^{-1} f θ − 1 = f K − 1 ∘ ⋯ ∘ f 1 − 1 x s a m p l e = f θ − 1 ( z s a m p l e ) \boldsymbol x_{sample} = f_\theta^{-1}(\boldsymbol z_{sample}) x s a m p l e = f θ − 1 ( z s a m p l e )
以下是一个使用 PyTorch 实现的简化版 RealNVP (一种基于耦合层的流模型) 的示例代码,用于二维数据分布的学习:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 import torchimport torch.nn as nnimport torch.optim as optimimport numpy as npimport matplotlib.pyplot as pltimport sklearn.datasets class CouplingLayer (nn.Module):def __init__ (self, input_dim, hidden_dim, parity ):super ().__init__()2 def forward (self, x, reverse=False ):2 , dim=-1 )if self.parity: if reverse: sum (dim=-1 )else : sum (dim=-1 ) if self.parity: 1 )else :1 )return y, log_det_jacobiandef inverse (self, y ):return self.forward(y, reverse=True )class NormalizingFlow (nn.Module):def __init__ (self, input_dim=2 , hidden_dim=256 , num_layers=6 ):super ().__init__()for i in range (num_layers):2 == 0 ))def forward (self, x ): 0 ], device=x.device)for layer in self.layers:return x, log_det_sumdef inverse (self, z ): 0 ], device=z.device) for layer in reversed (self.layers): return z, log_det_sumdef sample_data (n_samples=1024 ):0.05 )return torch.tensor(data, dtype=torch.float32)def loss_function (z, log_det_jacobian, prior ):sum (dim=-1 ) + log_det_jacobianreturn -log_likelihood.mean()def train_flow (dim=2 , num_epochs=10000 , batch_size=512 , lr=1e-3 ):8 , hidden_dim=128 )print ("开始训练 Flow 模型..." )for epoch in range (num_epochs):1.0 ) if (epoch + 1 ) % 500 == 0 :print (f"Epoch [{epoch+1 } /{num_epochs} ], Loss: {loss.item():.4 f} " )print ("训练完成!" )return flow_model, priordef visualize_results (flow_model, prior, data_samples, num_generated_samples=1000 ):eval () 18 , 6 ))1 , 3 , 1 )0 ], data_samples[:, 1 ], s=10 , alpha=0.5 , c='blue' )"Original Data Distribution (Moons)" )"x1" )"x2" )2 , 3 )1.5 , 2 )with torch.no_grad():1 , 3 , 2 )0 ], z_transformed[:, 1 ], s=10 , alpha=0.5 , c='green' )"Data Mapped to Latent Space (Z)" )"z1" )"z2" )3 , 3 , 100 ), np.linspace(-3 , 3 , 100 ))0.5 * (xx**2 + yy**2 )) / (2 * np.pi)5 , alpha=0.3 , cmap='gray' )4 , 4 )4 , 4 )with torch.no_grad():1 , 3 , 3 )0 ], x_generated[:, 1 ], s=10 , alpha=0.5 , c='red' )"Generated Data from Latent Samples" )"x1" )"x2" )2 , 3 )1.5 , 2 )if __name__ == '__main__' :2 , num_epochs=10000 ) 1000 )