Flow Models
taxonomy
从模型结构来说,主流的生成模一般可以分成以下几种:GAN,VAE,Flow,Diffusion
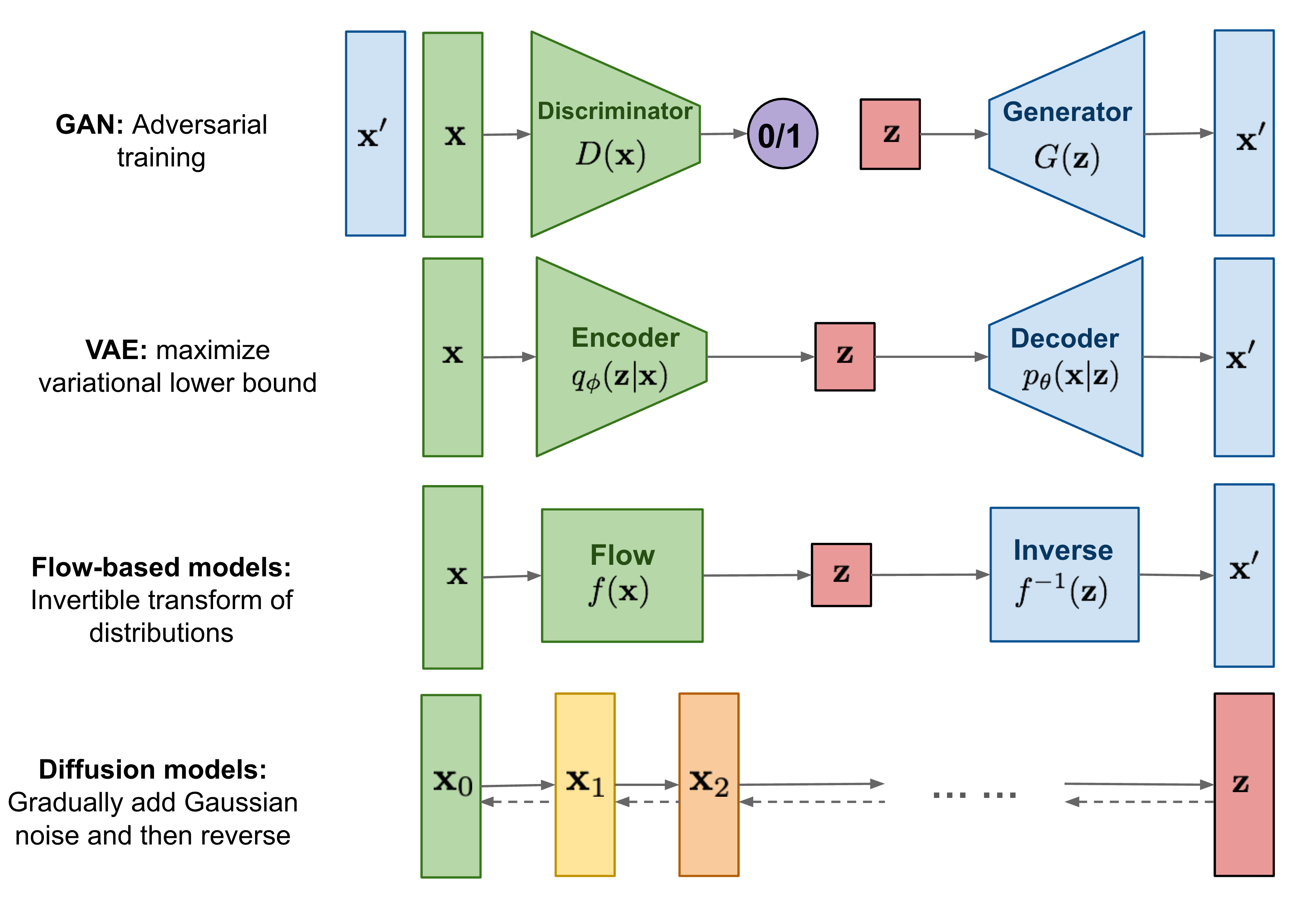
也有一种分类方法把 Component-by-Component(Auto-regressive model,例如 PixelRNN,VAR,NAR 等)的生成式模型也单独划分成一类,但是个人感觉这种分类方式不一样,上面模型的架构都可以应用于 VAR 类型的生成,因此个人感觉这是一种单独的分类方法
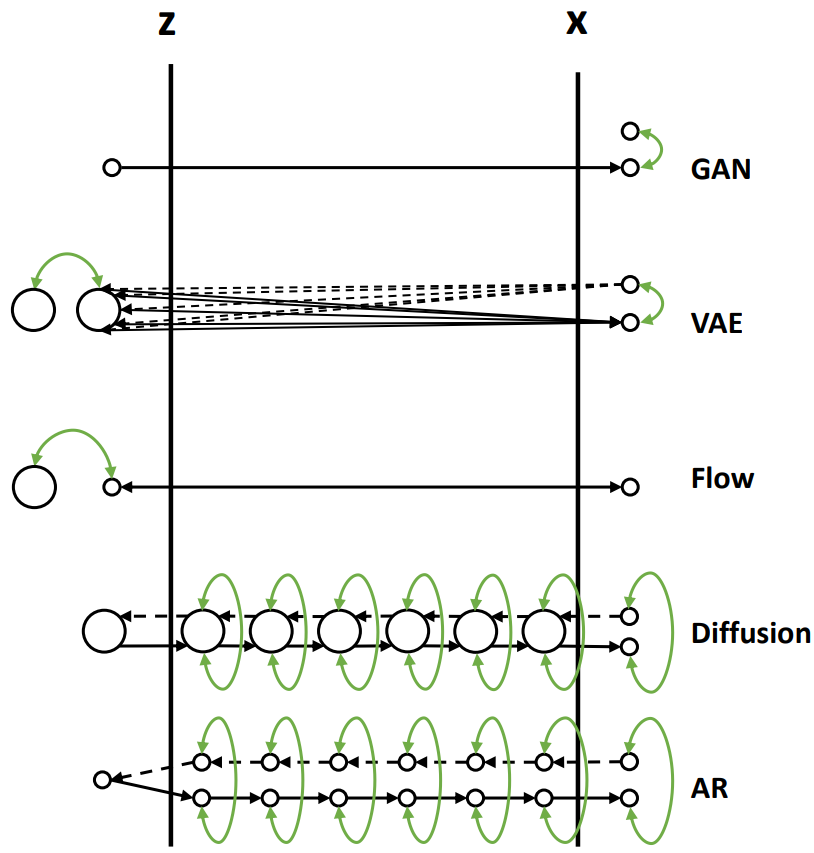
Preliminary
基于流的生成模型(Flow-based Generative Model)。先首先需要回顾一下之前的相关内容,生成式模型的目标就是通过生成器学习得到一个生成分布,并使其尽可能的接近于真实的数据分布。对于该过程我们可以表述为以下的公式:
G∗=∼argGmaxi=1∑mlogPG(xi){x1,x2,…,xm from Pdata}argGmax∫logpG(x)dx
定义隐空间和图像空间的两个概率密度函数为 π(z) 和 pG(x),这两个概率密度分布存在以下变换关系 x=G(z),其中 G 是一个生成函数,可以得到关系式:
π(z0)=pG(x0)∣det(Jf)∣
其中 Jf 为函数 f 的雅可比矩阵,可以进一步得到:
pG(x0)=π(z0)∣det(Jf−1)∣
则优化目标可以转化:
G∗==∼argGmax∫logpG(x)dxargGmax∫log(π(z)∣det(Jf−1)∣)dzargGmaxi=1∑m[logπ(G−1(z))+log∣det(Jf−1)∣]
在网络上的教程都忽略了一点,那就是雅可比矩阵其实是一个函数,对于一般的非线性模型,∣det(Jf−1)∣ 并不是一个定值,在这里这样处理的原因我们后续会对应回来,flow 其实是一个线性的模型
可逆变换的数学本质
流模型的核心在于建立双射映射函数 f:X→Z,通过雅可比行列式实现概率密度的精确变换
logpX(x)=logpZ(f(x))+log∣detJf(x)∣
这里需要强调几个关键点
- 雅可比矩阵的动态性:不同于线性代数中的常数矩阵,这里的Jf(x)是输入相关的函数矩阵,其计算复杂度直接影响模型可行性
- 维度保持特性:与VAE的隐空间压缩不同,流模型要求输入输出维度严格一致,这既是约束也是优势
- G 无需训练:由于 Flow 模型完全保证了可逆的转化,因此不需要类似 VAE 一样同时训练一个 encoder 和 decoder,只需要训练一个 G−1
Normalizing Flow
类似 VAE 的思想,我们强制隐空间内的概率分布为一个正态分布
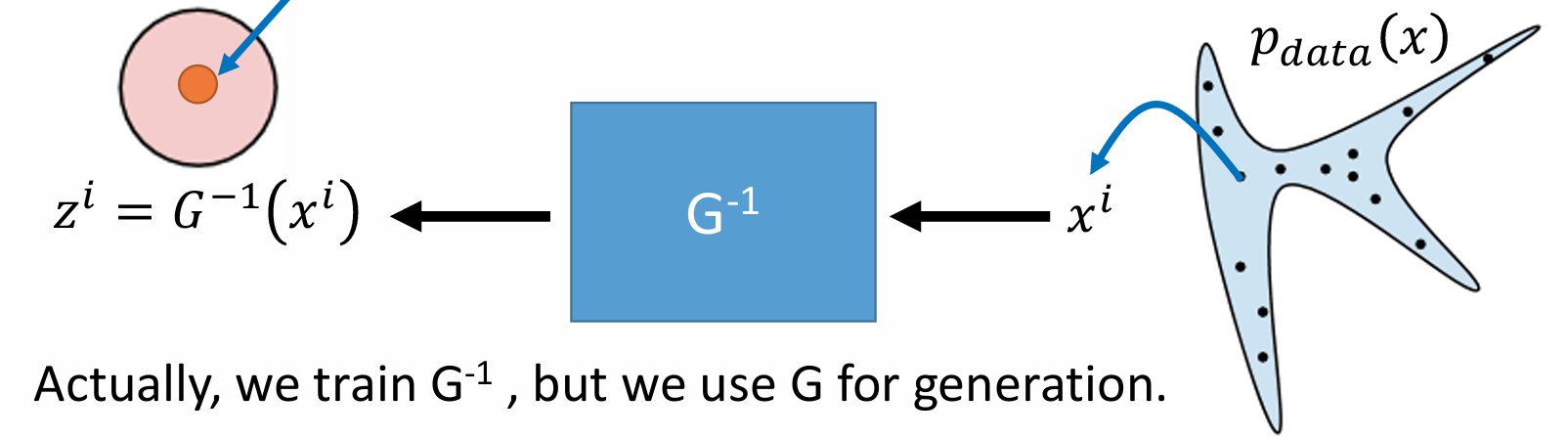
由于单个 G 受到了较多的约束(可逆,线性),所以可能表征能力有限,需要注意的是这里的 G 是可以进行多层扩展的,其对应的关系式只要进行递推便可

优化目标变为:
p1(xi)=p2(xi)=…logpk(xi)π(zi)∣det(JG1−1)∣π(zi)∣det(JG1−1)∣∣det(JG2−1)∣=logπ(zi)+h=1∑Klog∣det(JGK−1)∣
可以注意到和 VAE 不同的是,在隐空间内的向量维度和原图像空间内维度相同,如果随意设计一般的 G,就会在计算行列式的时候导致极大的计算量,总结上面的部分,我们需要对 G 的设计有如下的要求:
- G 是线性的,而且必须可逆
- G 的设计要考虑计算量,因此可以考虑特殊的设计方式来减少 det(G) 的计算
Coupling Layer
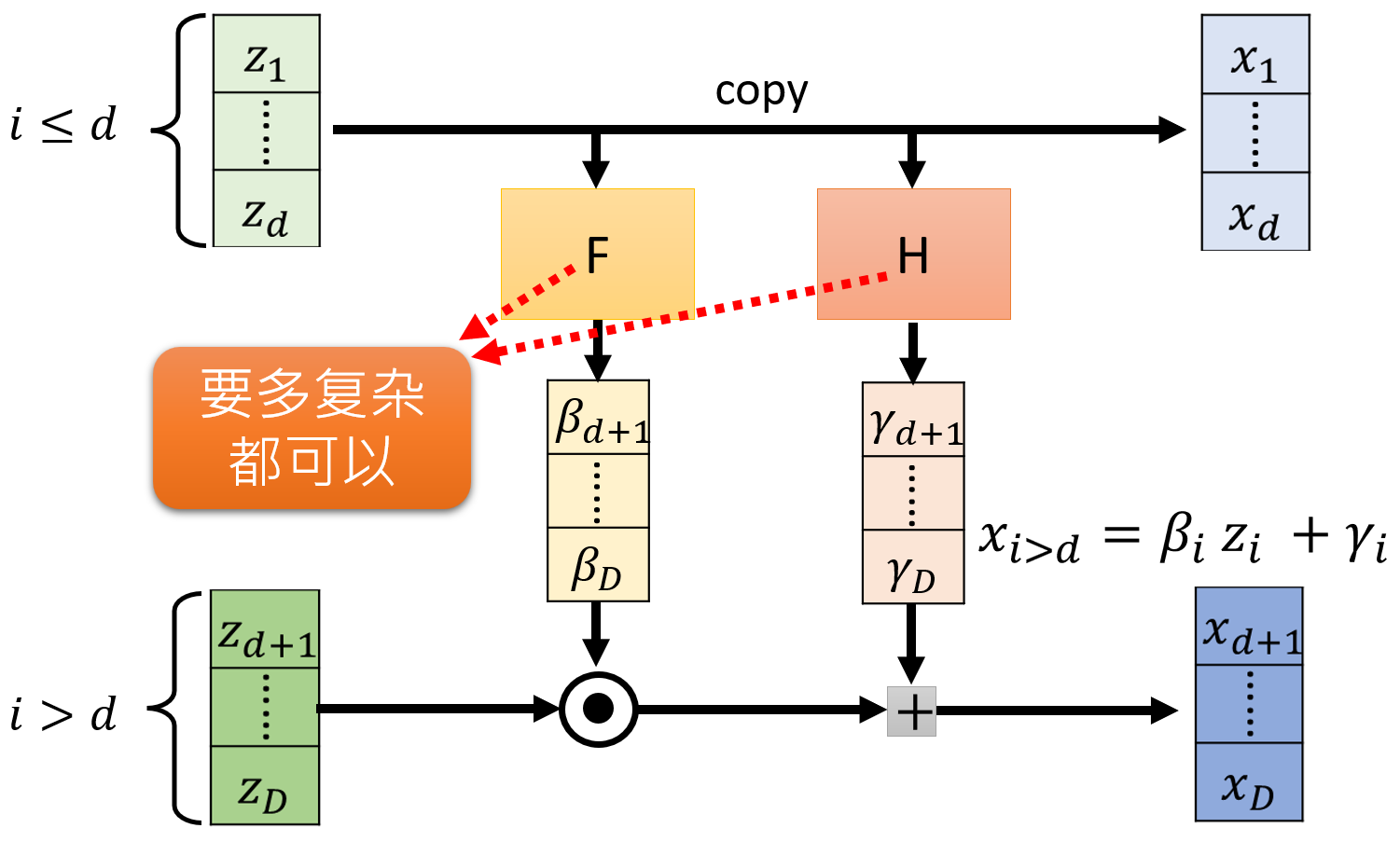
xi>d=βzi+γi⇒zi>d=βixi−γi
对于一层的 G 可以像如下进行如下计算行列式 JG :
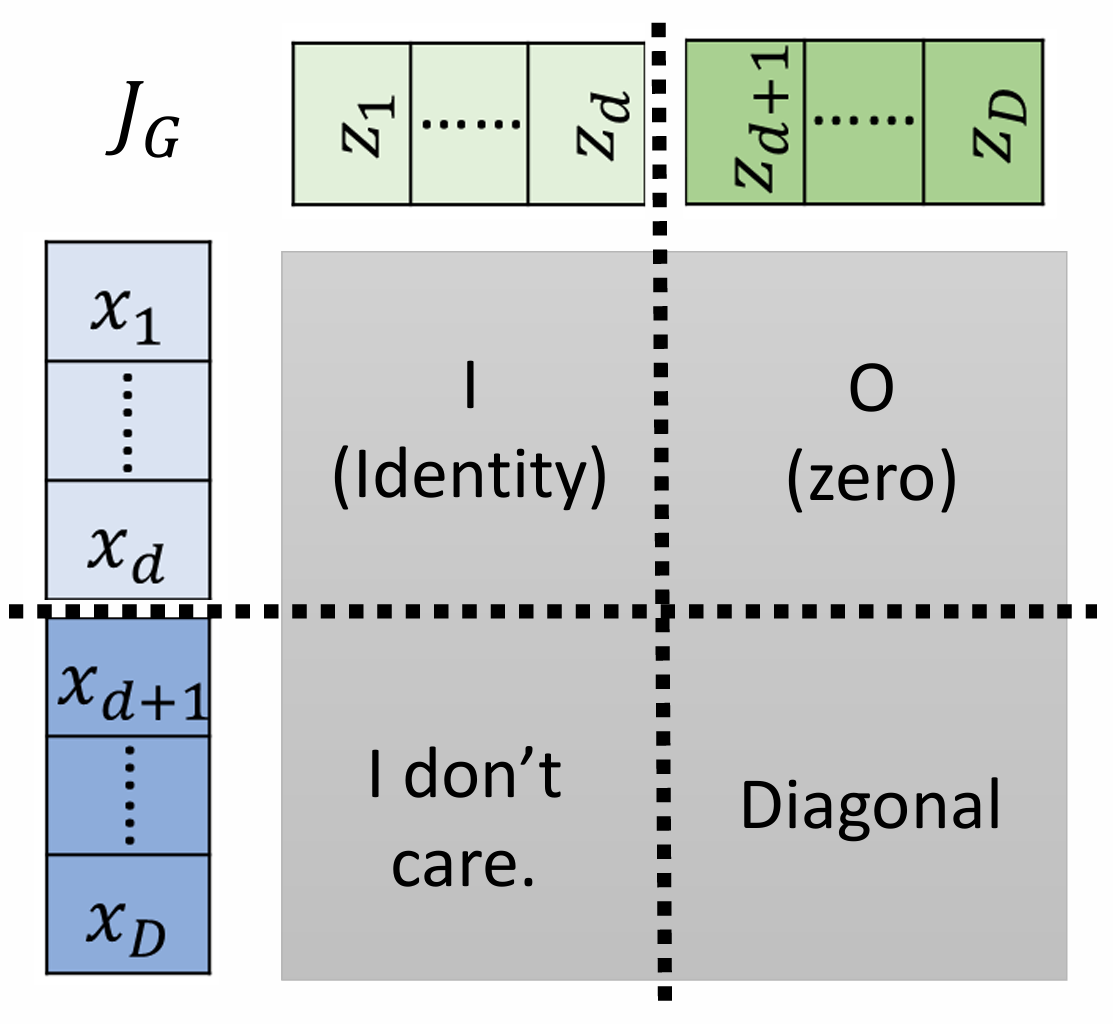
JG=[Id∂x1:d∂yd+1:D0d×(D−d)diag(exp(s(x1:d)))]
则行列式可以如下计算
det(JG)==∂zd+1∂xd+1∂zd+2∂xd+2…∂zD∂xDβd+1βd+2⋯βD
将 G 进行堆叠,同时对图像分成两个 couple:
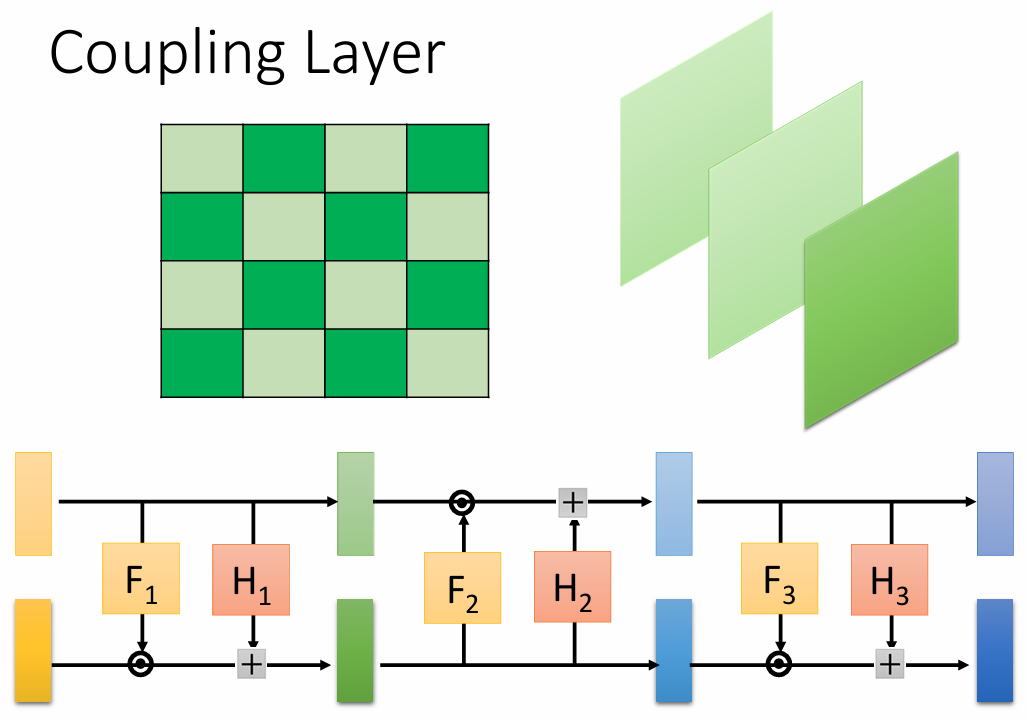
Train & Inference
Train
Flow model 采用严格的极大似然准则,目标函数为负对数似然:
Lflow=−Ex∼pdata[logpX(x)]=−Ex∼pdata[logpZ(f(x))+l=1∑Llog∣detJfl(xl)∣]
其中包含两个核心项:
- 先验匹配项:logpZ(f(x)) 驱动隐空间分布逼近标准正态分布
- 流形校正项:行列式项实质在度量流形变换的体积变化率
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
| import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
class CouplingLayer(nn.Module):
def __init__(self, dim, parity):
super().__init__()
self.parity = parity
self.net = nn.Sequential(
nn.Linear(dim//2, 50),
nn.ReLU(),
nn.Linear(50, dim//2)
)
def forward(self, x):
x = x if self.parity == 0 else torch.flip(x, [1])
xa, xb = torch.chunk(x, 2, dim=1)
params = self.net(xa)
s, t = torch.chunk(params, 2, dim=1)
self.log_det = (s.abs().clamp(min=1e-8).log()).sum(1)
yb = xb * torch.exp(s) + t
y = torch.cat([xa, yb], 1)
return y if self.parity == 0 else torch.flip(y, [1])
class NormalizingFlow(nn.Module):
def __init__(self, dim=2, num_layers=4):
super().__init__()
self.layers = nn.ModuleList()
for i in range(num_layers):
self.layers.append(CouplingLayer(dim, i%2))
def forward(self, x):
log_det_sum = 0
for layer in self.layers:
x = layer(x)
log_det_sum += layer.log_det
return x, log_det_sum
def sample_data(n_samples=1000):
data = sklearn.datasets.make_moons(n_samples=n_samples, noise=0.05)[0]
return torch.tensor(data, dtype=torch.float32)
def loss_function(z, log_det, prior):
log_pz = prior.log_prob(z).sum(1)
return -(log_pz + log_det).mean()
def train_flow():
dim = 2
flow_model = NormalizingFlow(dim=dim)
prior = torch.distributions.Normal(torch.zeros(dim), torch.ones(dim))
optimizer = optim.Adam(flow_model.parameters(), lr=1e-3)
for epoch in range(5000):
data = sample_data(512)
z, log_det = flow_model(data)
loss = loss_function(z, log_det, prior)
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(flow_model.parameters(), 1.0)
optimizer.step()
train_flow()
|






