planning

Planning：概念、分类与价值

引言

在强化学习领域，“planning”（规划）是智能体通过内部模拟环境进行决策的能力。与直接通过环境交互的试错学习不同，规划让智能体能够在「想象」中预演未来可能发生的场景。

即：Planning 指智能体利用环境模型（model）在内部生成虚拟经验，通过模拟状态转移和奖励反馈来优化策略的过程。其本质是通过「思维实验」降低对真实环境交互的依赖

1.2 与学习的区别

维度	Planning	Learning
数据来源	内部模型生成	真实环境交互
计算开销	前期模型构建成本高	后期策略优化成本高
典型方法	动态规划、MCTS	Q-learning、PG

例如，我们可以类似对标 Q-learning 算法创造 Q-planning 算法：

重复以下步骤：

随机选择一个状态 $s \in S$ 和一个动作 $a \in \mathcal{A}(S)$

把 $( s, a )$ 输入采样模型，然后获得采样得到的奖励 $r$ 和下一个状态 $s'$

对 $( s, a, r, s' )$ 进行一时间步表格 Q 学习： $Q(s, a) \leftarrow Q(s, a) + \alpha \left[ r + \gamma \max_{a'} Q(s', a') - Q(s, a) \right]$

规划方法的双重维度

规划分为状态空间的规划（state-space planning）和规划空间（plan-space planning）的规划：

状态空间的规划(state-space planning)：在状态空间搜索最佳策略，这是最常见的
规划空间的规划(plan-space planning)：在规划空间搜索最佳策略，包括遗传算法和偏序规划。这时，一个规划就是一个动作集合以及动作顺序的约束，这时的状态就是一个规划，目标状态就是能完成任务的规划

在连续状态空间（或者很大的状态空间）中，智能体不可能能把所有的状态-动作数据全部收集到，好的规划能够对环境进行提前的建模，能够让模型做出一些靠谱的泛化

Dyna 算法

Dyna 算法由强化学习先驱 Richard Sutton 提出，重要性在于统一了实时学习（learning）与离线规划（planning）。该架构创造性地让智能体能够：

从真实交互中学习（环境反馈）
从想象中学习（模型模拟）
两类经验并行处理实现知识融合

算法工作流程

graph LR
    A[真实经验] --> B[更新Q值]
    A --> C[更新环境模型]
    C --> D[模拟经验生成]
    D --> E[模型规划更新Q值]
    B --> F[策略改进]
    E --> F

真实经验同时用于模型的学习和直接的强化学习：

planning

维度	Dyna-Q	传统Q-learning
样本效率	1次交互触发n次更新	1次交互对应1次更新
收敛速度	快3-5倍（迷宫实验）	基础速度基准
模型依赖性	需要构建状态转移模型	无需环境模型

可以类似构建 Dyna-Q 算法：

Dyna-Q

规划与学习进一步融合：决策时规划

实时动态规划（DTDP）

实时动态规划（Real-Time Dynamic Programming）是针对大规模状态空间和实时决策需求设计的规划范式。与传统动态规划遍历所有状态的「地毯式搜索」不同（尽管动态规划相比于传统的其他算法可以减少计算量，但是他仍然是把所有的状态全部遍历了一遍的），RTDP采用聚焦更新策略：

状态更新优先级：仅更新智能体当前遭遇的状态及其可达后续状态
启发式引导：利用启发函数 $h(s)$ 引导搜索方向，避免无效状态探索

这种方式极大地减少了状态空间，AlphaGo 中使用的技术就是使用了 DTDP 而非传统的 DP

与传统动态规划的对比

维度	RTDP	传统DP（值迭代）
计算复杂度	$O(k)$ 每次更新k个相关状态	$O(N)$ 全状态空间遍历
内存占用	仅需存储活跃状态值	需存储全状态空间值
适用场景	在线实时决策（如自动驾驶）	离线规划（如棋类求解）
收敛条件	$\epsilon$ -收敛于最优策略	严格收敛到最优策略
典型更新方式	异步更新	同步全局更新

def rtdp(s_init, env, max_depth=100):
    V = defaultdict(float)  # 动态构建值函数表
    s = s_init
    for _ in range(max_depth):
        # 前向搜索阶段
        path = []
        while not env.is_terminal(s):
            a = greedy_policy(s, V)  # 基于当前V选择动作
            s_next = env.sample_next_state(s, a)
            path.append((s, a))
            s = s_next
        
        # 反向传播更新
        for (s_back, a_back) in reversed(path):
            # 只更新遍历过的状态
            V[s_back] = max([Q_value(s_back, a, V, env) 
                           for a in env.actions(s_back)])

决策时规划

这里我们又提出了一个新的概念：决策时规划。我们现在将规划分为两类：

背景规划（back ground planning）：规划用于更细你很多状态值共后续动作的选择，例如 Dyna，Q-planning 等。在前面，我们提到的算法全部被划分为背景规划
决策时规划（decision time planning）：规划只着眼于当前状态的动作选择。目前火爆的 world model 视频生成器就可以认为是一个用于决策时规划的模型（为自动驾驶服务），最终目的就是给一个 insight 的启发式函数来指导决策

Tree Search

一句话来概括：背景规划用于规划所有状态下的对象，而决策时规划只用于给出当前状态下对环境的启发式函数（类似启发式搜索，性能的提升不是来自于多步更新，而是来自于专注于当前状态的后续可能）

为了介绍 MCMC 方法，我们需要先介绍一下 Rollout 算法和

Rollout 算法：

Rollout 算法是一种用于强化学习中的策略评估和优化的方法。它通过从当前状态下进行模拟的蒙特卡洛估计，选取最高估计值的动作，是一种决策是规划的算法，表现取决于蒙特卡洛算法的估值的准确性

就是一种树搜索算法，将所有的轨迹展开到叶子节点并选择一个最优的轨迹，这种算法相当的低效，可以限制搜索的最大深度进行截断（将后续的值代替回报）来减少计算量（类似 beam search）

蒙特卡洛数搜索（Monte Carlo Tree Search）：

选择：根据树策略（动作值函数）遍历树到一个叶节点
扩展：从选择的叶节点出发选择未探索过的动作到达新的状态
模拟：从新的状态出发按照 rollout 策略进行轨迹模拟
回溯：得到的回报回溯更新树策略，rollout 访问的状态值不会被保存
重复上述步骤直至计算资源耗尽，从根节点选择最优动作
得到新状态，保留原有树的新状态下的部分节点
重复上述步骤直至游戏结束

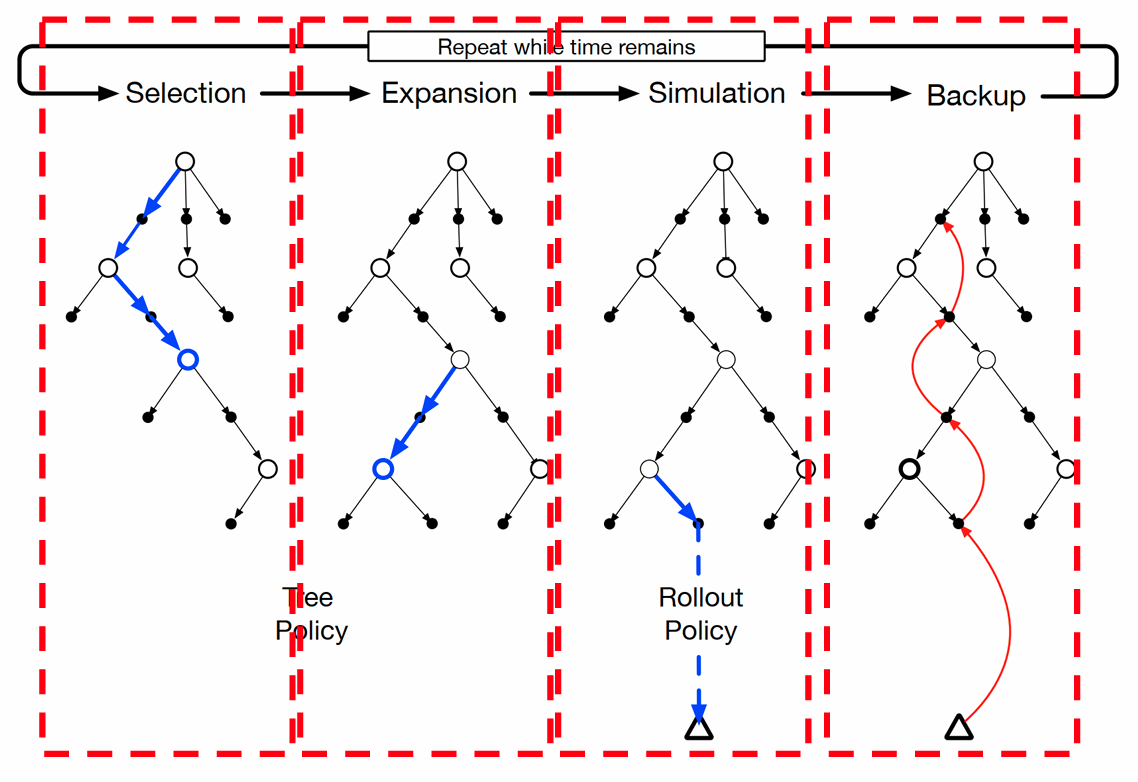
就是按照一种特定的方式进行树展开，然后使用 roll out 算法对展开的节点进行值估计，可以认为是启发式搜索和 rollout 的一种结合（探索和利用的结合）

ViT-Adapter复现下一篇