MDP的进一步思考

序列回报的形式：

​ 问题描述：为何序列回报 $G_t$ 的形式是通过指数加权求和衰减，即是通过将当前时刻及之后的所有奖励进行加权求和得到的：

$$G_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots = \sum_{k=0}^{\infty} \gamma^k R_{t+k}$$

​ 关于这个的定义来源，我们需要先明确我们的要求是什么，我们的需求是用一个值函数去评判序列的好坏，即我们需要构建序列之间的全序，即是对任意两个序列，需要有孰好孰坏之分，这种好坏有两种要求：

• 奖励更多的序列值函数更好：$[1,2,3] \prec [2,3,4]$
• 根据时间衰减的原则，相同回报下近期的回报比远期回报好：$[1,0,0] \prec [0,0,1]$

定理

​ 如果希望对于序列有全序，并满足以下性质：

$$[a_1, a_2, \cdots] < [b_1, b_2, \cdots] \Leftrightarrow [r, a_1, a_2, \cdots] < [r, b_1, b_2, \cdots]$$

那么序列回报形式只会是上述 $\gamma-$ 衰减求和形式。

证明思路

如果有 $a_0 + \gamma_1 a_1 > b_0 + \gamma_1 b_1 \Leftrightarrow r + \gamma_1 a_0 + \gamma_2 a_1 > r + \gamma_1 b_0 + \gamma_2 b_1$

那么 $(a_0 - b_0) + \gamma_1 (a_1 - b_1) > 0 \Leftrightarrow \gamma_1 (a_0 - b_0) + \gamma_2 (a_1 - b_1) > 0$

因此 $\gamma_2 = \gamma_1^2$ 后续时间步的 $\gamma_t$ 可以以此类推

策略与占用度量

价值函数的重构

考虑折扣回报的期望：

\begin{align*} V^\pi(s_0) &= \mathbb{E}_\pi\left[ \sum_{t=0}^\infty \gamma^t r(S_t,A_t) \right] \\ &= \sum_{t=0}^\infty \gamma^t \mathbb{E}_\pi[r(S_t,A_t)] \quad \text{(期望线性性)} \\ &= \sum_{t=0}^\infty \gamma^t \sum_{s,a} P^\pi(S_t=s, A_t=a)r(s,a) \\ &= \frac{1}{1-\gamma} \underbrace{(1-\gamma)\sum_{t=0}^\infty \gamma^t \sum_{s,a} P^\pi(S_t=s, A_t=a)r(s,a)}_{\sum_{s,a}\rho^\pi(s,a)r(s,a)} \end{align*}

最终得到价值函数的密度表达：

$$\boxed{V^\pi = \frac{1}{1-\gamma}\sum_{s,a}\rho^\pi(s,a)r(s,a)}$$

对偶视角

• 原始优化问题（策略空间）：

$$\max_\pi \mathbb{E}_\pi\left[\sum_{t=0}^\infty \gamma^t r(S_t,A_t)\right]$$

• 对偶问题（占用度量空间）：

$$\max_\rho \sum_{s,a} \rho(s,a)r(s,a) \quad \text{s.t.} \quad \begin{cases} \rho(s,a) \geq 0 \\ \sum_a \rho(s,a) = (1-\gamma)\mu_0(s) + \gamma\sum_{s',a'} \rho(s',a')P(s|s',a') \end{cases}$$

为策略优化提供对偶空间视角：

graph TD
    A[原始空间] -->|策略参数θ| B[价值最大化]
    C[对偶空间] -->|占用度量ρ| D[约束满足]
    B <-->|强对偶性| D

$\mathcal{D}$为满足贝尔曼流约束的可行域。这种视角为：

• 策略梯度方法提供理论支撑
• 原始-对偶优化算法奠定基础
• 安全约束处理开辟新路径

强对偶性证明思路：

1. 构造拉格朗日函数，引入状态分布的约束
2. 通过对偶变量将约束转化为惩罚项
3. 证明原始问题与对偶问题的最优值相等

​ 在前面分析过，策略空间和占用度量空间是存在双射关系的，即 $\pi$ 和 $\rho^\pi$ 一一对应，当策略进行更新的时候，占用度量的更新是不可知的（除非非常简单的情况），因此强化学习优化策略的难点在于，如何在改变策略的时候能优化问题，因此在优化策略的时候，我们需要对策略进行策略评估（policy evaluation）和策略提升（policy improvement）

​ 其中用于策略评估的方法就是动作值函数和状态值函数，下面我们定义策略提升

策略提升（policy improvement）

定义

​ 对于两个策略 $\pi$ 和 $\pi'$，如果满足如下性质，称 $\pi'$ 是 $\pi$ 的策略提升：

• 对于任何状态 $s$（所有的 state 均满足），有

$$Q^\pi(s, \pi'(s)) \geq V^\pi(s)$$

​ 这个式子的含义是，只在当前一步进行策略改变，而在后续决策过程中策略仍然不变，如果这一步策略改变能够带来更高的值函数，那么策略就称之为提升了

---

一些思考

​ 实际上我觉得这个式子存在不严谨的地方，实际上我认为在数学上应该这样写：

$$\mathbb{E}_{\pi'}[Q^\pi(s, \pi'(s))|S_t=s] \geq V^\pi(s)$$

$Q^\pi$ 的定义中只对状态转移取期望，而 $\pi'$ 如果是一个随机策略的话，$Q^\pi(s, \pi'(s))$ 就不是一个确定的值了，所以正确写法是否应该是上面的期望表达式。但是在主流的强化学习课本上都写的是没有取期望的表达式，应该是默认的期望表达式

---

策略提升定理 (Policy Improvement Theorem)

​ 对于两个策略 $\pi$, $\pi'$，如果满足如下性质：对于任何状态 $s$，有 $Q^\pi(s, \pi'(s)) \geq V^\pi(s)$，则有 $V^{\pi'}(s) \geq V^\pi(s)$，则称 $\pi'$ 是 $\pi$ 的策略提升

• 证明：

$$\begin{aligned} V^\pi(s) &\leq Q^\pi(s, \pi'(s)) \\ &= \mathbb{E}_{\text{Env}}[R_t + \gamma V^\pi(S_{t+1}) | S_t = s, A_t = \pi'(s)] \\ &= \mathbb{E}_{\pi'}[R_t + \gamma V^\pi(S_{t+1}) | S_t = s] \\ &\leq \mathbb{E}_{\pi'}[R_t + \gamma Q^\pi(S_{t+1}, \pi'(S_{t+1})) | S_t = s] \\ &= \mathbb{E}_{\pi'}[R_t + \gamma \mathbb{E}_{\text{Env}}[R_{t+1} + \gamma V^\pi(S_{t+2}) | S_{t+1}, A_{t+1} = \pi'(S_{t+1})] | S_t = s] \\ &= \mathbb{E}_{\pi'}[R_t + \gamma R_{t+1} + \gamma^2 V^\pi(S_{t+2}) | S_t = s] \\ &\leq \mathbb{E}_{\pi'}[R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \gamma^3 V^\pi(S_{t+3}) | S_t = s] \\ &\cdots \\ &\leq \mathbb{E}_{\pi'}[R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \gamma^3 R_{t+3} + \cdots | S_t = s] \\ &= V^{\pi'}(s) \end{aligned}$$

• 需要注意的是，$\mathbb{E}_{\pi'}[R_t + \gamma V^\pi(S_{t+1}) | S_t = s]$ 这一步求期望的下标 $\pi'$ 这个策略只影响一步的采样，即 $t$ 时刻的动作 $a_t$ 的采样，后续执行的策略仍然是 $\pi$

$$\forall s\in \mathcal{S}, Q^\pi(s,\pi'(s)) \ge V^\pi(s)\\ \Rightarrow \forall s\in \mathcal{S}, V^{\pi'}(s) \ge V^\pi(s)$$

在一个点上可以更新策略那么对于整个策略空间都可以去更新，那么更新策略就需要做两件事：

• 估计每个 value function
• 基于 value function 寻找到了策略提升点

则就可以更新我们的策略

举例：$\epsilon$-greedy 的策略提升

$\epsilon$-greedy 策略描述为：

$$\pi(a|s) = \begin{cases} \epsilon/m + 1 - \epsilon & \text{if } a^* = \arg\max_{a \in A} Q(s, a) \\ \epsilon/m & \text{otherwise} \end{cases}$$

​ 如果另一个 $\epsilon$-Greedy 策略 $\pi'$是基于 $Q^\pi$ 的提升，那么有 $ V^{\pi’}(s) \geq V^\pi(s) $：

$$\begin{aligned} V^{\pi'}(s) \geq Q^\pi(s, \pi'(s)) =& \sum_{a \in A} \pi'(a|s) Q^\pi(s, a)\\ \text{$m$ actions}=& \frac{\epsilon}{m} \sum_{a \in A} Q^\pi(s, a) + (1 - \epsilon) \max_{a \in A} Q^\pi(s, a)\\ \geq& \frac{\epsilon}{m} \sum_{a \in A} Q^\pi(s, a) + (1 - \epsilon) {\color{red}\sum_{a \in A} \frac{\pi(a|s) - \epsilon/m}{1 - \epsilon}} Q^\pi(s, a)\\ =& \sum_{a \in A} \pi(a|s) Q^\pi(s, a) = V^\pi(s) \end{aligned}$$

​ 这里有一个构造性的证明，实际上这个证明就是前面的策略提升定理中的证明特殊化为 $\epsilon$-greedy 策略了

​ 这里容易产生一个问题，$\epsilon$-greedy 策略根本没变啊，为什么说它是策略提升了，实际上策略是依赖于值函数的，这里策略的提升含义是值函数进行优化了，间接导致在 state $s$ 下的策略优化了

MDP 的优化：策略迭代与价值迭代

策略迭代

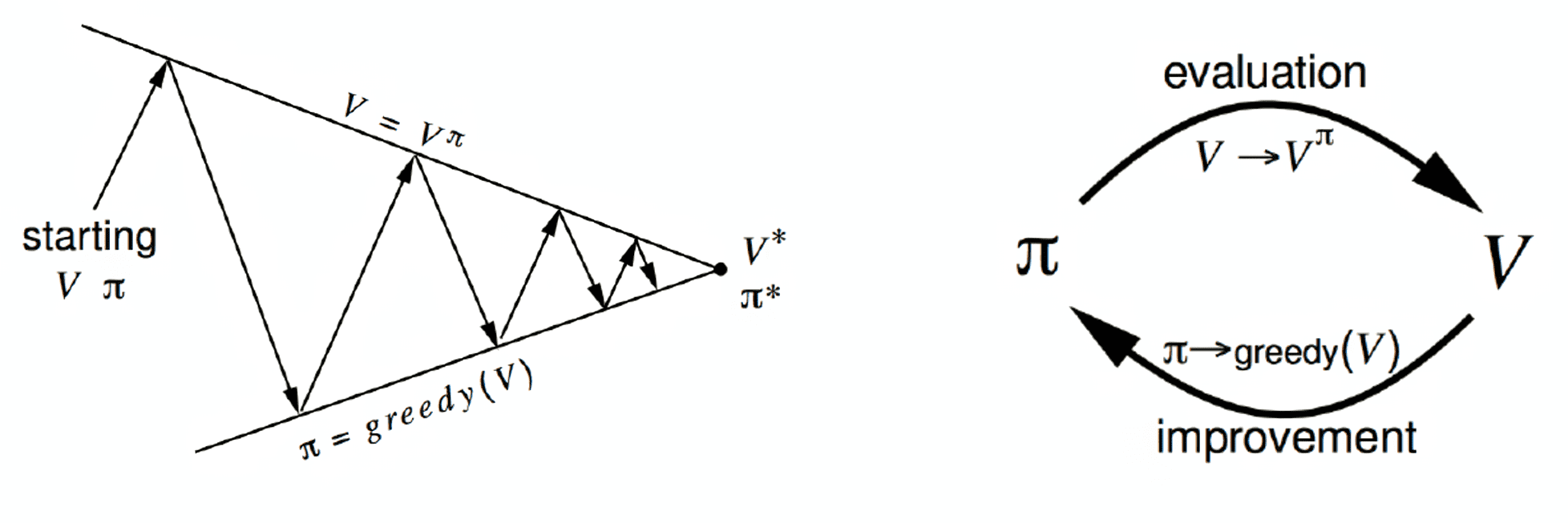
策略迭代（Policy Iteration）包含两个交替的步骤：

• 策略评估（Policy Evaluation）：在给定一个策略的情况下，通过迭代计算该策略的价值函数（即每个状态的长期期望回报）。
• 策略改进（Policy Improvement）：基于当前策略的价值函数，通过选取每个状态下能最大化价值的动作来生成新的策略。

策略迭代需要显式地维护一个策略，并通过评估和改进交替进行，直到策略收敛到最优策略

策略迭代过程（基于价值 $V$ 函数）：

1. 随机初始化策略 $\pi$
2. 循环直到收敛：
   • 计算 $V:=V^\pi$（策略评估）
   • 对于每个状态，更新策略：$\pi'(s)=\arg\max_{a} \left[r(s,a)+\gamma\sum_{s'}P(s')V(s')\right]$（策略改进）

​ 在上面的算法中 $V$ 的更新是相当耗时的，因此策略迭代算法显著慢于价值迭代算法。同时，策略改进的理论基础就是策略提升定理，保证了这样更新策略是在优化策略

​ 值得一提的是，这样 greedy 的更新策略在实际中存在问题，在 MDP 的理论推导中所有的状态都能兼顾到，但是在实际中因为强化学习中数据十分有限，对于无模型（model free）的强化学习方法，兼顾探索于利用是非常重要的，就不使用 greedy 了

价值迭代

​ 在策略迭代中可以观察到，虽然策略评估函数 $V^\pi$ 没有收敛到最优值，但是策略已经改进到了最佳的策略。再加上策略评估的计算量尤其大，因此可以考虑能否将策略评估去掉

​ 价值迭代（Value Iteration）将这两个步骤合并到了一起。它直接通过贪心算法尝试找到每个状态下的最优行动，从而更新每个状态的价值函数（让价值函数快速收敛）。在每次迭代中：

价值迭代过程（基于价值 $V$ 函数）：

1. 对于每个状态，初始化 $V^\pi(s)=0$

2. 循环直到收敛：

   ​ 对于每个状态，更新价值：$V(s)=r(s)+\arg\max_{a} \gamma\left[\sum_{s'}P(s')V(s')\right]$（策略改进）

​ 值得一提的是，$V(s)$ 没有策略 $\pi$ 的角标，因为这里的 $V^\pi(s)$ 并不对应任何策略的值函数，他只是一个计算中间量（这里没有一个显示的策略），它的迭代过程可以用下图表述：

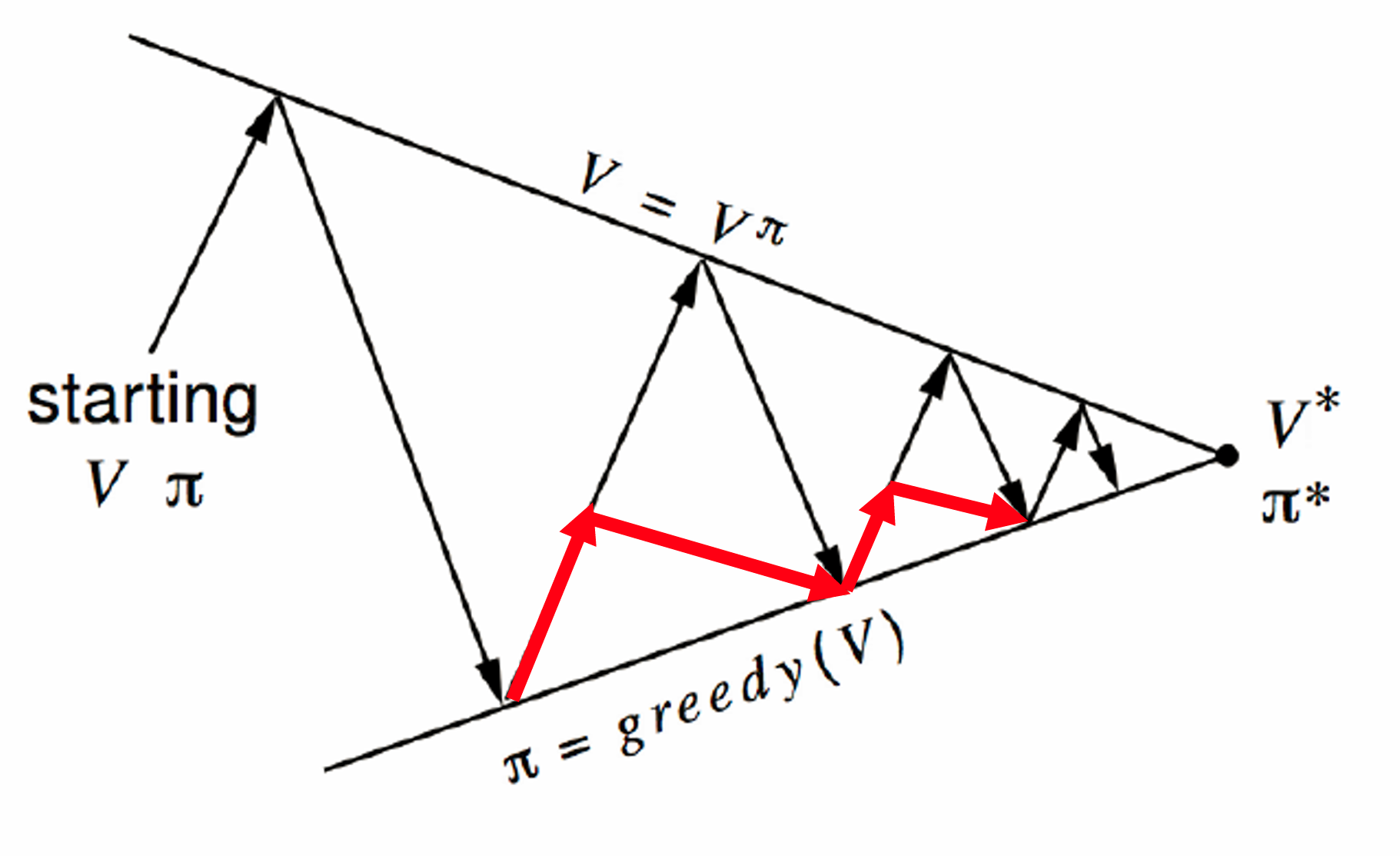
因此价值迭代方法是一个更实际的方法，有如下一半的规律：

• 价值迭代是贪心更新法，相当于策略评估中进行一轮价值更新，然后直接根据更新后的价值进行
  策略提升
• 策略迭代中，用 Bellman 等式更新价值函数代价很大
• 对于空间较小的MDP，策略选代通常很快收敛
• 对于空间较大的MDP，价值迭代更实用（效率更高）
• 如果没有状态转移循环，最好使用价值迭代