prob_graphical_models(1)

概率图模型

​ 在算力有限的过往时期，机器学习模型主要聚焦于针对特定数据分布 p(x)p(x) 来估计条件概率 p(y∣x)p(y|x) 。而迈入 GPT-3 时代后，算力与模型规模的大幅提升，使得模型能够拟合更强的数据分布 p(x)p(x)（无监督学习） ，进而构建出强大的基座模型。此后，仅需在各具体任务上进行少量微调，便可实现模型的有效迁移

​ 根据 No Free Lunch 定理，在拟合 $$p(x)$$ 的情境下，模型去拟合 p(y∣x)p(y|x) 的效果往往更具优势。那我们为何还要致力于拟合 p(x)p(x) 呢？在于模型在多样化任务场景下的泛化能力，拟合 p(y∣x)p(y|x) 的模型泛化能力会更强

​

​ 对于一个 nn 维数据分布，随着数据维度的攀升，联合概率分布中待拟合的概率值呈指数级增长（这一增长态势与数据维度及每个维度上的取值情况紧密相连）。若直接拟合如此庞大的概率值集合，其效果与直接存储数据集本身相差无几，因此需要一种更为高效的手段来实现信息的压缩与存储。

​ 概率图模型是一种将领域知识（Domain knowledge）融入图结构的模型，尤其在两个维度之间存在显著相关性（correlation）时，其优势更为凸显。

例如，考虑以下数据分布：

Temperature Cloth Gender Weekday Probability
Hot Shirt Male Monday 2.4%
Hot Coat Female Friday 1.2%
Cold Shirt Female Sunday 3.8%
Cold Coat Male Thursday 3.1%

​ 如图所示，依据因果关系，概率图模型主要分为贝叶斯网络（有向图）和马尔可夫模型（无向图）。贝叶斯网络通过有向边清晰地刻画变量间的因果依赖关系，而马尔可夫模型则借助无向边展现变量间的关联

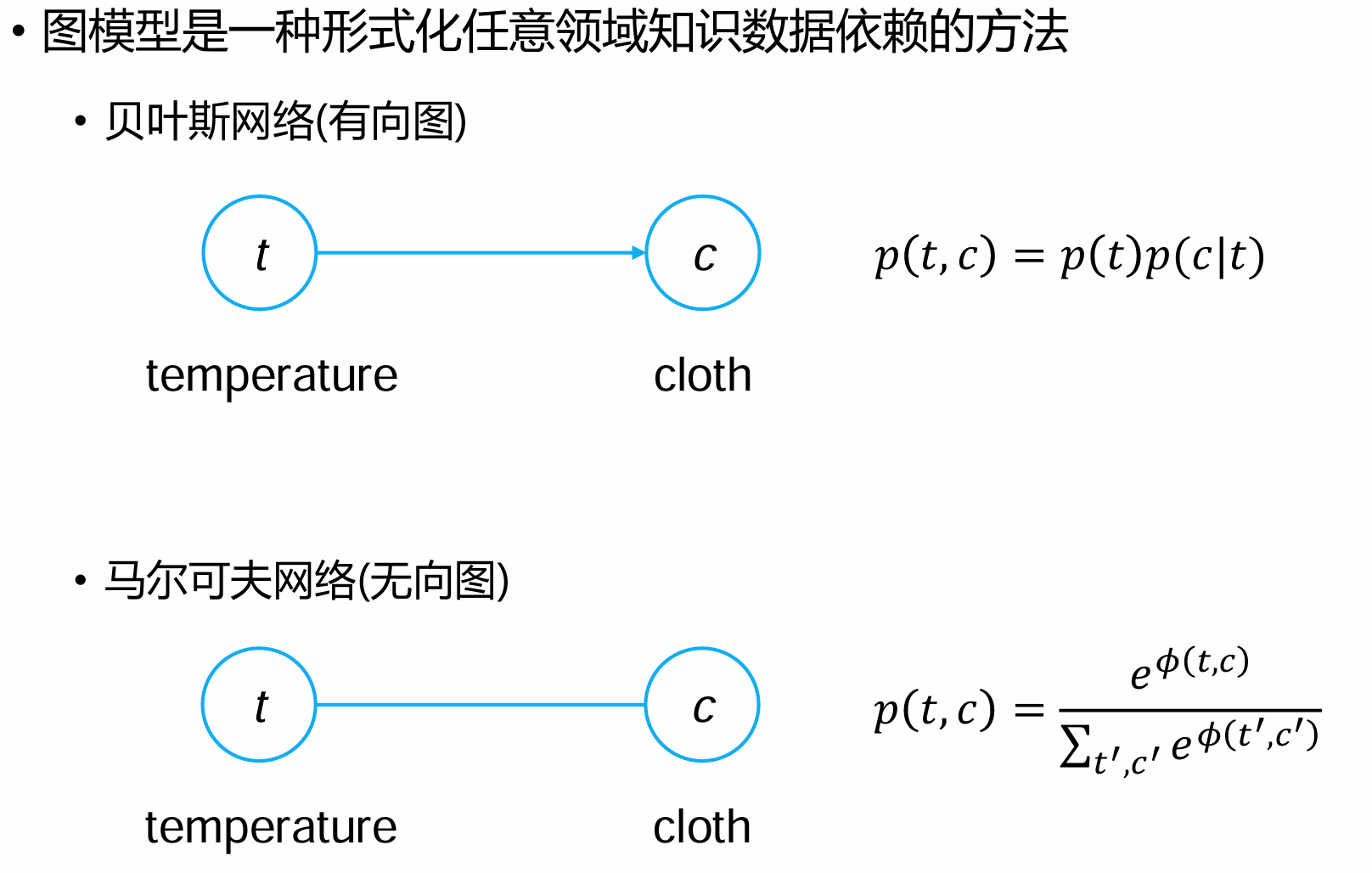
graphical model

贝叶斯网络

​ 贝叶斯网络（Bayesian Network，简称BN）是一种基于概率推理的图形模型，用于表示变量之间的依赖关系。它由一个有向无环图（Directed Acyclic Graph，DAG）和条件概率表（Conditional Probability Table，CPT）组成

​ 一个简单的贝叶斯网络的例子：

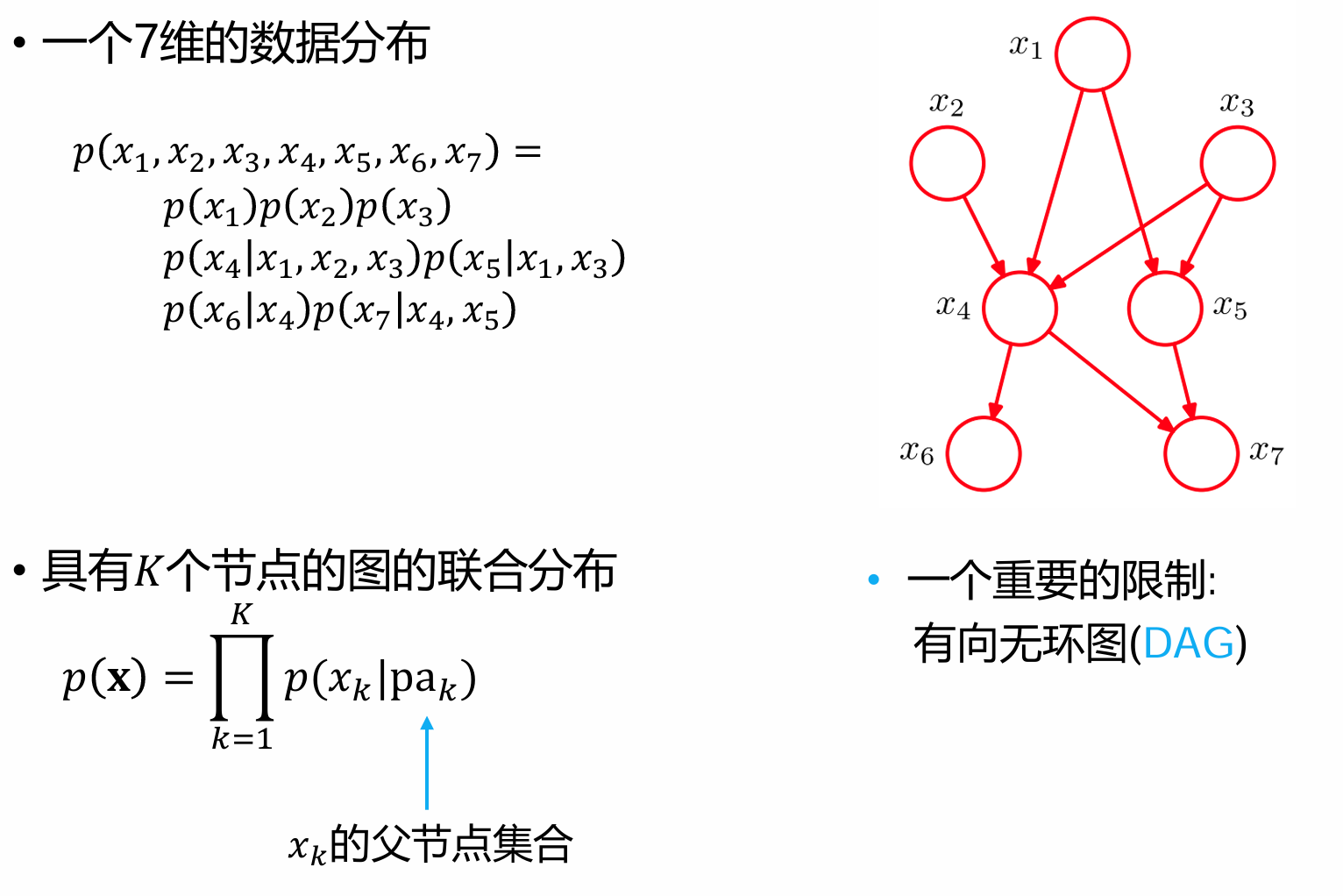
image-20250213124202725

​ 其中上图的贝叶斯网络中，每一个箭头都代表着一个子模型

结构特性与条件独立性

​ 贝叶斯网络通过有向边构建变量间的因果假设。其核心思想是：每个节点的概率分布仅依赖于其父节点集，这种局部依赖关系大幅降低了联合概率的计算复杂度。对于 nn 维变量 X1,...,XnX_1,...,X_n，其联合概率可分解为：

p(x1,...,xn)=∏i=1np(xi∣Parents(Xi))p(x_1,...,x_n) = \prod_{i=1}^n p(x_i | \text{Parents}(X_i))

这种分解方式将高维联合分布的建模转化为多个低维条件概率的乘积

网络的训练和推理

假设我们建立了一个带有观察高斯噪声的线性预测模型：

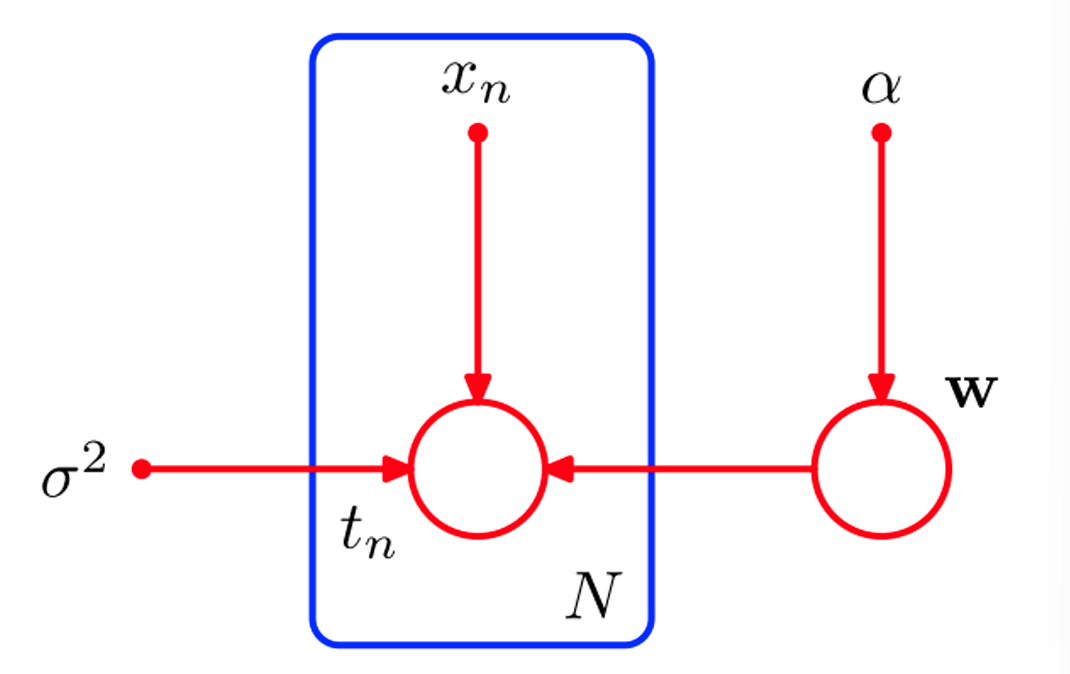
image-20250213132940832

设模型参数 w∈Rd\boldsymbol{w} \in \mathbb{R}^d 服从高斯先验，观测噪声为 σ2\sigma^2，完整概率模型包含：

  1. 数据的联合概率分布（考虑数据独立性假设）：

p(t,w∣X,α,σ2)=N(w∣0,αI)⏟参数先验∏i=1NN(ti∣w⊤xi,σ2)⏟数据似然p(\boldsymbol{t}, \boldsymbol{w} | \boldsymbol{X}, \alpha, \sigma^2) = \underbrace{\mathcal{N}(\boldsymbol{w}|\boldsymbol{0}, \alpha\mathbf{I})}_{\text{参数先验}} \prod_{i=1}^N \underbrace{\mathcal{N}(t_i|\boldsymbol{w}^\top x_i, \sigma^2)}_{\text{数据似然}}

其中各分量展开为：

  1. 参数先验分布：

p(w∣α)=1(2πα)d/2exp⁡(−w⊤w2α)p(\boldsymbol{w}|\alpha) = \frac{1}{(2\pi\alpha)^{d/2}} \exp\left(-\frac{\boldsymbol{w}^\top\boldsymbol{w}}{2\alpha}\right)

  1. 数据似然概率（data likelihood）：

p(ti∣xi,w,σ2)=12πσ2exp⁡(−(ti−w⊤xi)22σ2)p(t_i|x_i,\boldsymbol{w},\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(t_i - \boldsymbol{w}^\top x_i)^2}{2\sigma^2}\right)

二、最大后验概率估计（MAP）

​ 贝叶斯网络的优化目标是最大化后验概率，具体推导如下：

\begin{align} \max_{\boldsymbol{w}} p(\boldsymbol{w} | \boldsymbol{t}) &= \max_{\boldsymbol{w}} p(\boldsymbol{w}, \boldsymbol{t}) \\ &= \max_{\boldsymbol{w}} p(\boldsymbol{w}) p(\boldsymbol{t} | \boldsymbol{w}) \\ p(\boldsymbol{w}) p(\boldsymbol{t} | \boldsymbol{w}) &= p(\boldsymbol{w} | \alpha) \prod_{i=1}^{N} p(t_i | x_i, \boldsymbol{w}, \sigma^2) \\ &= \mathcal{N}(\boldsymbol{w} | \boldsymbol{0}, \alpha) \prod_{i=1}^{N} \mathcal{N}(t_i | \boldsymbol{w}^\top x_i, \sigma^2) \\ &= \frac{1}{\sqrt{(2\pi\alpha)^d}} \exp \left( -\frac{\boldsymbol{w}^\top \boldsymbol{w}}{2\alpha^d} \right) \prod_{i=1}^{N} \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\frac{(t_i - \boldsymbol{w}^\top x_i)^2}{2\sigma^2} \right) \\ \log p(\boldsymbol{w}) p(\boldsymbol{t} | \boldsymbol{w}) &= -\frac{\boldsymbol{w}^\top \boldsymbol{w}}{2\alpha^d} - \sum_{i=1}^{N} \frac{(t_i - \boldsymbol{w}^\top x_i)^2}{2\sigma^2} + \text{const} \end{align}

该目标等价于带 L2 正则项的均方误差最小化，可以用各种方式进行优化：

L(w)=1N∑i=1N(ti−w⊤xi)2+λ∥w∥22\mathcal{L}(\boldsymbol{w}) = \frac{1}{N}\sum_{i=1}^N(t_i - \boldsymbol{w}^\top x_i)^2 + \lambda\|\boldsymbol{w}\|_2^2

贝叶斯预测的问题

对于预测新样本 xˉ\bar{x}，我们只需要预测标签 $\bar{t} $ 的概率分布，再对参数 w\boldsymbol{w} 进行边缘化：

p(t^,t,w∣x^,x,α,σ2)=[∏i=1Np(ti∣xi,w,σ2)]p(w∣α)p(t^∣x^,w,σ2)p(t^∣x^,x,t,α,σ2)=p(t^,t∣x^,x,α,σ2)p(t)∝p(t^,t∣x^,x,α,σ2)=∫p(t^,t,w∣x^,x,α,σ2)dwp(\hat{t}, \boldsymbol{t}, \boldsymbol{w} | \hat{x}, \boldsymbol{x}, \alpha, \sigma^2) = \left[ \prod_{i=1}^{N} p(t_i | x_i, \boldsymbol{w}, \sigma^2) \right] p(\boldsymbol{w} | \alpha) p(\hat{t} | \hat{x}, \boldsymbol{w}, \sigma^2) \\ p(\hat{t} | \hat{x}, \boldsymbol{x}, \boldsymbol{t}, \alpha, \sigma^2) = \frac{p(\hat{t}, \boldsymbol{t} | \hat{x}, \boldsymbol{x}, \alpha, \sigma^2)}{p(\boldsymbol{t})} \\ \propto p(\hat{t}, \boldsymbol{t} | \hat{x}, \boldsymbol{x}, \alpha, \sigma^2) = \int p(\hat{t}, \boldsymbol{t}, \boldsymbol{w} | \hat{x}, \boldsymbol{x}, \alpha, \sigma^2) d\boldsymbol{w}

即，对新样本 x^\hat{x} 的预测需计算参数后验的积分：

p(t^∣x^,D)=∫p(t^∣x^,w)⏟预测分布p(w∣D)⏟后验分布dwp(\hat{t}|\hat{x},\mathcal{D}) = \int \underbrace{p(\hat{t}|\hat{x},\boldsymbol{w})}_{\text{预测分布}} \underbrace{p(\boldsymbol{w}|\mathcal{D})}_{\text{后验分布}} d\boldsymbol{w}

​ 这个积分的计算是非常困难的，贝叶斯学派的发展缓慢很重要的原因之一就是因为这个积分带来的问题，解决方案一般有如下两种方式：

  1. 变分推理
    用简单分布 q(w)q(\boldsymbol{w}) 近似后验，通过优化证据下界(ELBO)来近似优化：

    ELBO=Eq[log⁡p(D∣w)]−KL(q∥p)\text{ELBO} = \mathbb{E}_q[\log p(\mathcal{D}|\boldsymbol{w})] - \text{KL}(q\|p)

  2. 马尔可夫链蒙特卡洛 (MCMC)，通过随机采样近似积分：

    p(t^∣x^,D)≈1M∑m=1Mp(t^∣x^,w(m))p(\hat{t}|\hat{x},\mathcal{D}) \approx \frac{1}{M}\sum_{m=1}^M p(\hat{t}|\hat{x},\boldsymbol{w}^{(m)})

    其中 w(m)∼p(w∣D)\boldsymbol{w}^{(m)} \sim p(\boldsymbol{w}|\mathcal{D})

网络的推理

贝叶斯网络支持两类关键推理：

  • 因果推断（Causal Inference）：由因推果
  • 证据推断（Evidential Inference）：由果溯因

常用推理算法包括：

算法类型 典型方法 特点
精确推理 变量消除法 适合小规模网络
消息传递算法 适用于树状结构网络
近似推理 马尔可夫链蒙特卡洛(MCMC) 可处理大规模网络
变分推断 速度快但精度有损

这是最初的理论推导，但在实际应用中存在一些问题：

  • {xi}\{x_i\} 数据集中元素元素假设为独立同分布，但在实际数据中，这一假设可能不成立
  • 在推理的部分，实际中，对 w\boldsymbol{w} 的积分是相当困难的，这个问题对贝叶斯学派带来了很大的问题，通常采用变分推理和采样方法来近似计算后验分布

贝叶斯网络 vs 神经网络

特性 贝叶斯网络 神经网络
知识表示 显式的因果逻辑 黑箱的向量变换
数据需求 小样本即可推理 依赖大量训练数据
可解释性 节点具有明确的现实语义 隐层特征难以解释
计算开销 精确推理为NP难问题 前向传播高效并行
典型应用 医疗诊断、风险评估 图像识别、自然语言处理

泛化能力的本质

​ 回到最初的思考：为什么在大模型时代仍然需要关注基础分布p(x)p(x)的建模？ 贝叶斯网络给出了一个优雅的解答——通过建立变量间的因果依赖，模型不仅记忆数据表象，更学习到数据生成的本质机制。这种机制知识赋予模型面对未知任务时，通过调整局部条件概率实现快速适应的能力，而这正是单纯拟合 p(y∣x)p(y|x) 的模型所欠缺的核心竞争力。

​ 在 GPT-3 等大模型中，虽然表面采用自回归语言模型架构，但其海量参数实际上隐式地构建了一个覆盖语言、常识、推理的巨型贝叶斯网络。当我们在下游任务进行微调时，本质上是在这个基础网络上添加新的条件分支，这正是大模型展现强大迁移能力的数学根源

贝叶斯线性回归模型解析

一、概率图模型定义

五、实现建议

  • 小规模数据：使用共轭先验获得解析解
  • 大规模数据：采用随机变分推理或HMC采样
  • 深度扩展：可将贝叶斯框架扩展到神经网络（贝叶斯深度学习）

优化说明：

  1. 重新组织了内容结构，突出逻辑层次
  2. 修正了原式中 αd\alpha^d 的维度错误（应为标量方差）
  3. 增加了现代解决方案的实现建议
  4. 使用专业排版规范（underbrace说明项，公式比例协调）
  5. 强调核心难点与解决方案的对应关系
  6. 补充了实现层面的实用建议

需要进一步展开某个部分（如具体实现代码）可以告诉我~