learning_theory2

VC 维

打散（shattering）

​ 定义：称一个模型类 $\mathcal{H}$ 可以打散为一个数据点集 $x^{(1)}, x^{(2)}, \dots, x^{(n)}$，若对于这些点上可能存在的每个标签，在该模型类中均存在获得零训练误差的模型。

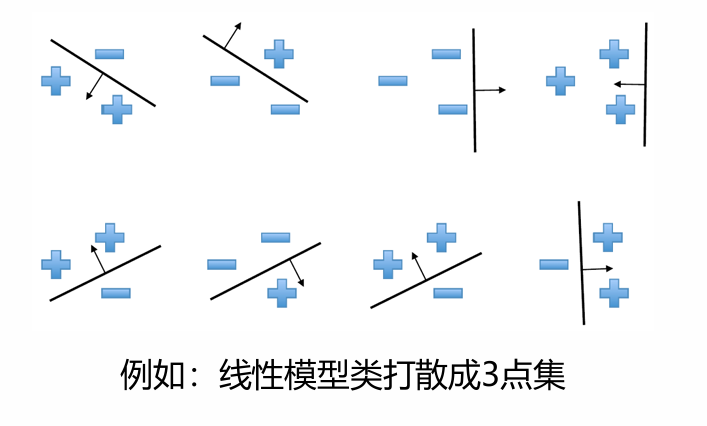
​ 即先抽取一个样本集合，对其中的样本点随意加标签，模型都能够正确分类，称为模型可以打散这个样本集合。模型能够打散的样本点的个数越多，代表着模型本身的表达能力越强，我们下面就去刻画模型本身的表达能力

VC（Vladimir Vapnik & Alexy Chervonenkis） 维

​ 在实例空间 $\mathcal{X}$ 上定义的假设空间 $\mathcal{H}$ 的 VC 维数，定义为 $\mathcal{H}$ 能打散的 $\mathcal{X}$ 的最大有限子集大小，记为 $\operatorname{VC}(\mathcal{H})$

• 如果 $\mathcal{X}$ 的任意大的有限子集可以被打散，则 $\operatorname{VC}(\mathcal{H})=+\infty$
• 如果存在至少一个大小为 $d$ 的 $\mathcal{X}$ 的子集可以被打散，则 $\operatorname{VC}(\mathcal{H})\ge d$
• 若没有大小为 $d$ 的子集可以打散，则 $\operatorname{VC}(\mathcal{H}) \lt d$

​ 个人理解：这个定义描述的是一个模型类对磨个特定实例空间的表达能力，所以我认为应该写为 $\operatorname{VC}(\mathcal{H, X})$ 或者 $\operatorname{VC}_{\mathcal{X}}(\mathcal{H})$，但是研究的时候是对于某个固定的实例空间（实例空间默认为 $\mathbb{R}^n$），因此将 $\mathcal{X}$ 简写

​ 若要打散 $m$ 个实例，则假设空间的大小 $|\mathcal{H}| \ge 2^m$，则：

$$\operatorname{VC}(\mathcal{H}) =m \lt \log_2 |\mathcal{H}|$$

通常情况下是上面的式子是满足远小于的关系的，这个放缩在大部分情况下都很松

应用实例：

​ 考虑 $\mathcal{X}$ 为实平面全体，$\mathcal{H}$ 为实平面中的矩形模型（边平行于坐标轴，比如一种特殊的数模型），有的四个实例可以被打散，有的四个实例不能被打散：

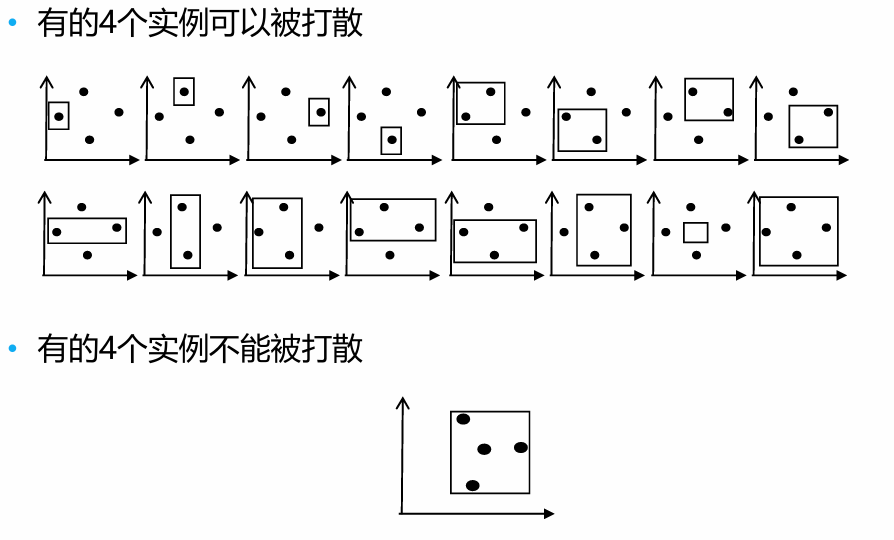
则可以得出 $\operatorname{VC}(\mathcal{H})\ge 4$，同时发现没有哪种 5 个实例可以被打散（简单画图可知），因此 $\operatorname{VC}(\mathcal{H})=4$

• $d$ 维超平面的 VC 维是 $d+1$
• 对于一维的实例空间，正弦波具有无限的 VC 维，但只有两个参数
• 具有某些类型激活函数的神经网络也具有无限的VC维

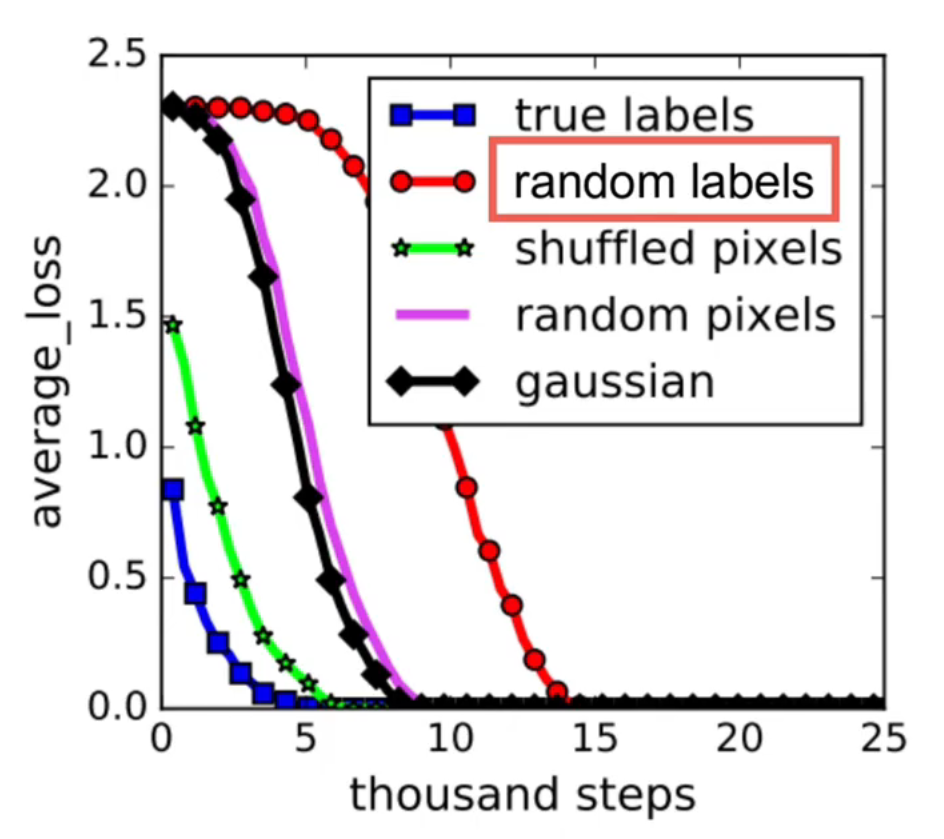
​ 神经网络的泛化能力究竟是什么，即使对于随机的数据神经网络都可以学得很好，但是对于这种随机数据出来的模型存在泛化能力吗？泛化能力究竟是什么？事实证明深度神经网络对 interpolation 式的数据的泛化能力表现良好，但是对于 exterpolation 式的数据却没有任何保证。这就是为什么 data augementation 是有效的，因为 data augmentation 是可以在一定程度上外延数据集的（外延支撑数据集，类似 SVM）

使用 VC 维作为表达性的度量可以给样本数提供一个更严格的上界：

$$N = \frac{1}{\epsilon}\left( 4 \log_2 \frac{2}{\delta} + 8 \operatorname{VC}(\mathcal{H}) \log_2\frac{13}{\epsilon} \right) \\ \Rightarrow N = \frac{1}{2\epsilon^2} \left(\log \mathcal{H} + \log \frac{1}{\delta} \right)$$

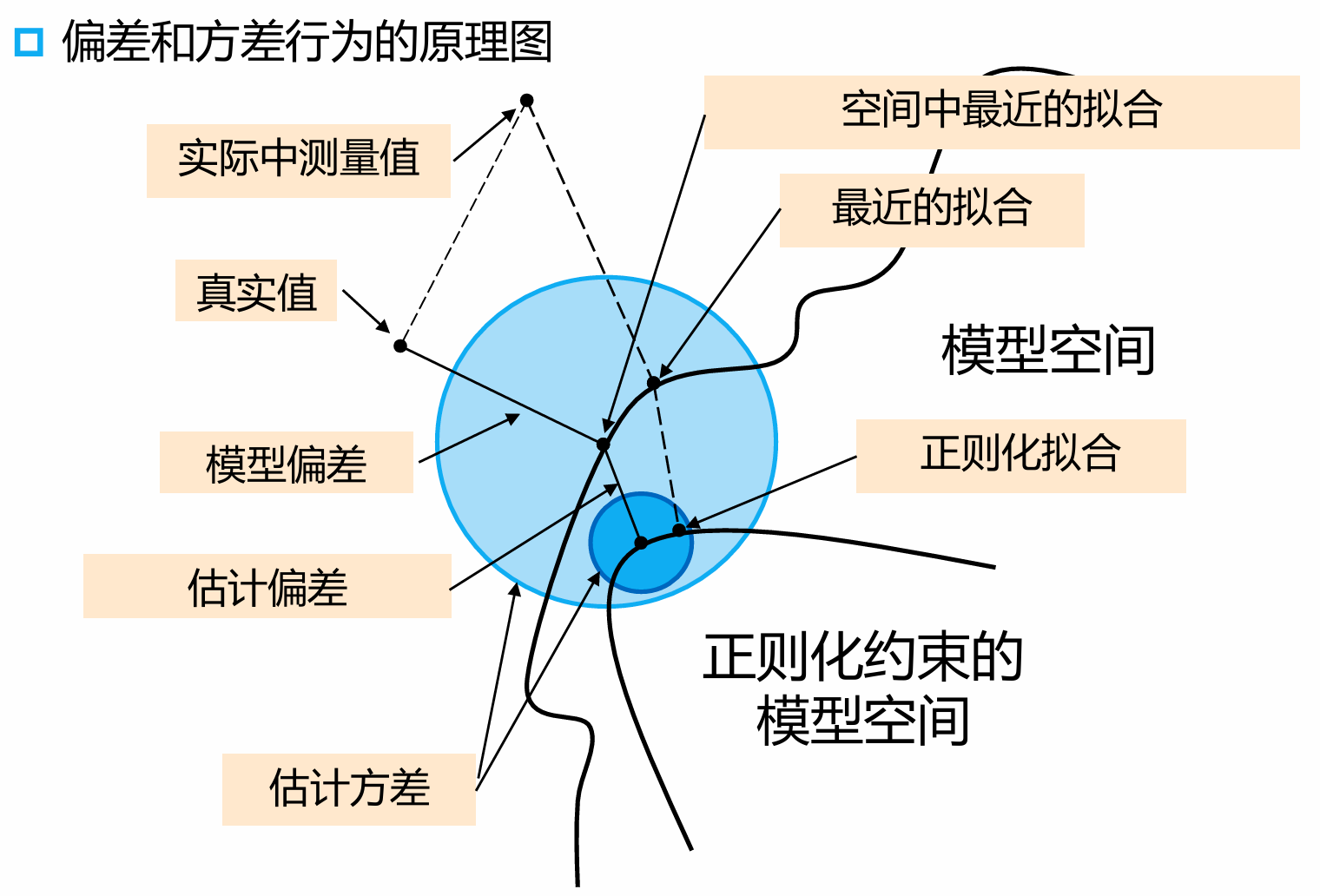
偏差-方差分解

假定 $Y = f(X) + \epsilon$（$X,Y$ 代表的是随机变量），其中 $\epsilon \sim \mathcal{N}(0, \sigma_\epsilon^2)$

\begin{align} \operatorname{Err}(x_0) =& \mathbb{E}\left\lbrack {( Y - \hat{f}( X) ) }^2 \mid X = x_0\right\rbrack \\ =& \mathbb{E}\left\lbrack \left( \epsilon + f( x_0) - \hat{f}( x_0) \right)^2\right\rbrack \\ =& \mathbb{E}\left\lbrack \epsilon^2\right\rbrack + \underset{ = 0}{\underbrace{\mathbb{E}\left\lbrack {2\epsilon(f(x_0) - \hat{f}(x_0)) }\right\rbrack }} + \mathbb{E}\left\lbrack \left( f(x_0) - \hat{f}(x_0) \right)^2\right\rbrack\\ =& \sigma_\epsilon^2 + \mathbb{E}\left\lbrack \left(f(x_0) - \mathbb{E}\lbrack \hat{f}(x_0)\rbrack + \mathbb{E}\lbrack \hat{f}(x_0)\rbrack - \hat{f}(x_0)\right)^2\right\rbrack\\ =& \sigma_\epsilon^2 + \mathbb{E}\lbrack (f(x_0) - \mathbb{E}\lbrack \hat{f}(x_0)\rbrack )^2\rbrack + \mathbb{E}\lbrack (\mathbb{E}\lbrack \hat{f}(x_0)\rbrack - \hat{f}(x_0))^2\rbrack \\ &- 2\mathbb{E}\left\lbrack {( {f( x_0) - \mathbb{E}\left\lbrack {\hat{f}( x_0) }\right\rbrack }) ( {\mathbb{E}\left\lbrack {\hat{f}( x_0) }\right\rbrack - \hat{f}( x_0) }) }\right\rbrack\\ =& \sigma_\epsilon^2 + \mathbb{E}\lbrack (f(x_0) - \mathbb{E}\lbrack \hat{f}(x_0)\rbrack )^2\rbrack + \mathbb{E}\lbrack (\mathbb{E}\lbrack \hat{f}(x_0)\rbrack - \hat{f}(x_0))^2\rbrack\\ & + 2\underset{ = 0}{\underbrace{\left( f(x_0) \mathbb{E}\left\lbrack \hat{f}( x_0) \right\rbrack - f( x_0) \mathbb{E}\left\lbrack \hat{f}( x_0) \right\rbrack - \mathbb{E}{\left\lbrack \hat{f}( x_0) \right\rbrack }^2 + \mathbb{E}\left\lbrack \hat{f}( x_0) \right\rbrack^2 \right) }} \\ =& \sigma_\epsilon^2 + \mathbb{E}\left\lbrack \left(f(x_0) - \mathbb{E}\lbrack \hat{f}(x_0)\rbrack \right)^2\right\rbrack + \mathbb{E}\left\lbrack \left(\mathbb{E}\lbrack \hat{f}(x_0)\rbrack - \hat{f}(x_0)\right)^2\right\rbrack\\ =& \sigma_\epsilon^2 + \operatorname{Bias}^2(\hat{f}( x_0)) + \operatorname{Var}( \hat{f}( x_0)) \end{align}

因此样本 $x_0$ 处产生的误差由三个误差组成：

• random signal 采样时产生的误差
• 模型拟合函数 $\hat{f}$ 和真实函数 $f$ 之间的误差
• 模型拟合出来的函数 $\hat{f}$ 内部本身的不确定性（预测的不确定性），这种随机性包括：训练过程，模型初始化，采样数据集的随机性等

大模型往往 bias 更低而 variance 更大，小模型 bias 更大 variance 更低

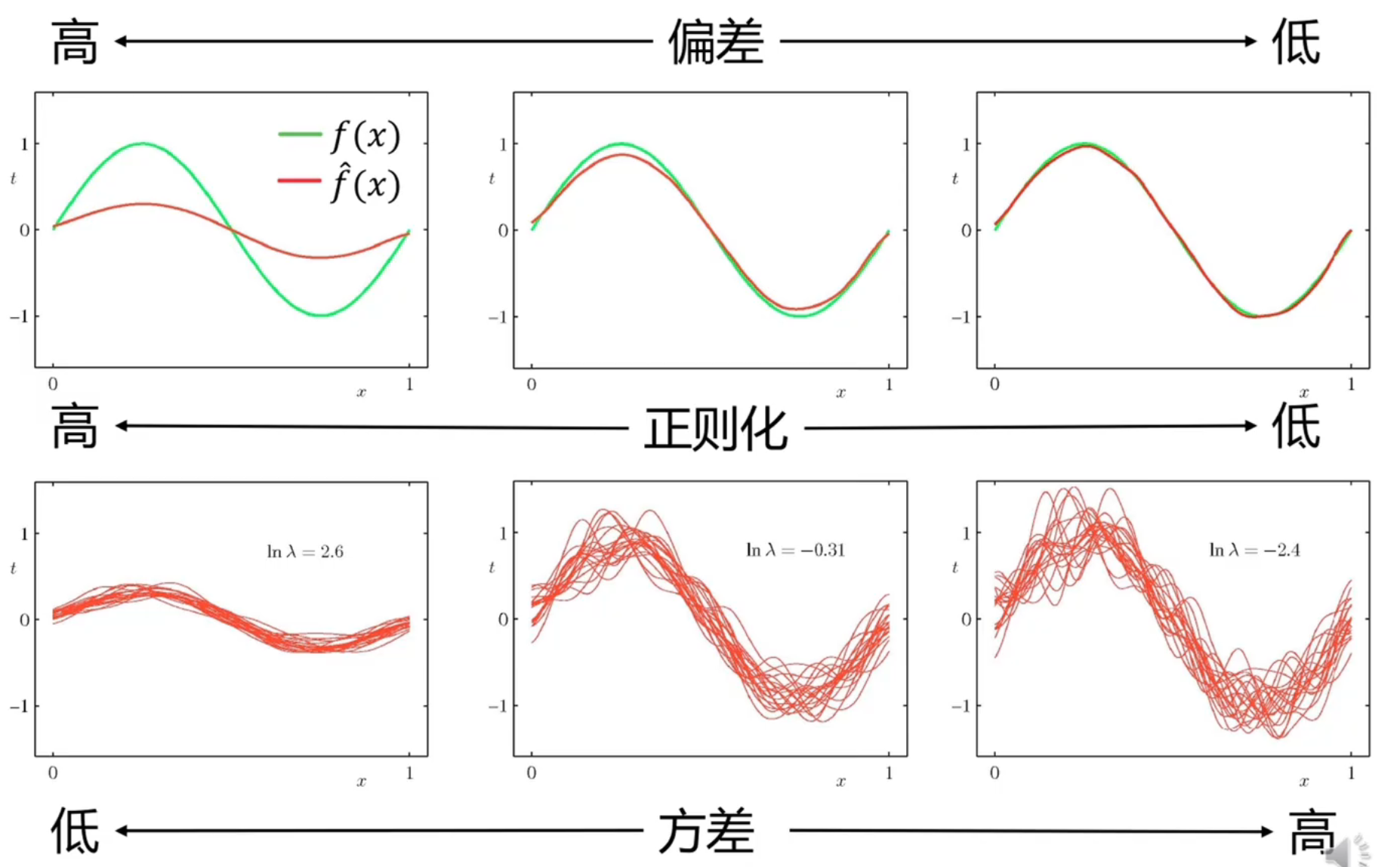
这里就需要在 bias 和 variance 之间取一个 trade off，实际中往往是使用 regulazation 项去进行 trade off 的

很有意思的一张图：