multi_task

多任务学习

​ 多任务学习（Multitask Learning, MTL）是一种机器学习方法，它试图通过同时学习多个相关任务来提高模型的性能。这种方法基于一个假设：即不同任务之间存在一定的关联或共享信息，通过共同学习这些任务可以互相帮助，提升彼此的表现

单一任务 vs. 多任务学习

定义一个单一任务：从单一输入源中学习单个输出目标。该任务的目标函数为：

$$\min_w \mathcal{L}(\boldsymbol X, \boldsymbol y, \boldsymbol w)$$

而多任务学习的目标函数则为：

$$\min_{\boldsymbol W = [\boldsymbol w^1,\dots, \boldsymbol w^M]} \sum_{m=1}^M \lambda_m \mathcal{L}(\boldsymbol X^m, \boldsymbol y^m, \boldsymbol w^m) + \mu \mathop{Reg}(\boldsymbol W)$$

其中，$\boldsymbol X^m$ 和 $\boldsymbol y^m$ 分别表示第 $m$ 个任务的输入和标签，$\mathop{Reg}$ 表示权重的正则化项。

为什么多任务学习有效？

直接将多个任务分开学习与同时学习的区别在于，后者能够利用任务之间的共性和差异性，从而同时解决多个学习任务，并在效率和效果（efficiency & performance）上优于单独训练多个模型。具体原因包括：

• 隐式的数据增广：通过共享一部分网络参数，在学习一个任务时也可以间接地对其他任务进行训练。这种机制不仅增加了样本的有效数量，还使得模型更具鲁棒性，因为它可以从不同的噪声模式中学习

• 知识窃取（Eavesdropping）：某些特征可能在一个任务中难以学习但在另一个任务中相对容易掌握。通过这种方式，可以在学习过程中互补彼此的优势。例如，在多任务密集预测中，边缘检测通常比分割更容易实现，但边缘特征对于分割同样至关重要。

• 表示偏差：每个任务都有自己的表示偏差，多任务学习可以通过多种视角下的特征学习，获得更为广泛和全面的特征表示

多任务学习的分类

根据不同任务的特征空间是否相同，多任务学习可以分为同构特征多任务学习和异构特征多任务学习：

• 同构特征多任务学习：不同任务的特征空间相同，即数据集分布一致。
• 异构特征多任务学习：不同任务的特征空间不相同。

默认情况下，我们假定多任务学习为同构特征多任务学习，因为其难度相对较小。

理解共享（share knowledge）

多任务学习中的共享主要体现在以下几个层次：

• 特征层次：不同任务的特征处理方式是否相同，例如使用相同的backbone
• 实例层次：预处理数据的方式是否相同，适用于异构特征任务的学习。
• 任务层次：网络参数是否共享，这一层面与其他两个层次有所重叠。

参数共享：

• 参数硬共享：就是共享一部分的网络，例如在 scene parsing 中使用相同 backbone
• 参数软共享：允许每个任务有自己的模型参数，但通过某种机制鼓励这些参数之间的相似性。与硬参数共享不同，软参数共享不强制要求某些网络层在所有任务间共享，软共享方式包括：权重转移（Transfer Learning），正则化方法等，正则化方法举例如下所示：

\begin{align} \min_{\boldsymbol w^1, \boldsymbol w^2} &\alpha \mathcal{L}_1(\boldsymbol y_1 + f_{\boldsymbol w^1}(\boldsymbol X_1))+ (1-\alpha)\mathcal{L}(\boldsymbol y_2, f_{\boldsymbol w^2}(\boldsymbol X_2)) \\ & + \underbrace{\lambda_1(\lVert \boldsymbol w^1 \rVert^2 + \lVert \boldsymbol w^2 \rVert)}_\text{regularization item} + \underbrace{\lambda_2 \lVert \boldsymbol w^1 - \boldsymbol w^2\rVert^2}_\text{soft share item} \end{align}

• 共享-私有方法：深度学习领域用得最广的方法，例子仍然可以使用 scene parsing，多任务使用相同的 backbone 但是具有不同的任务头

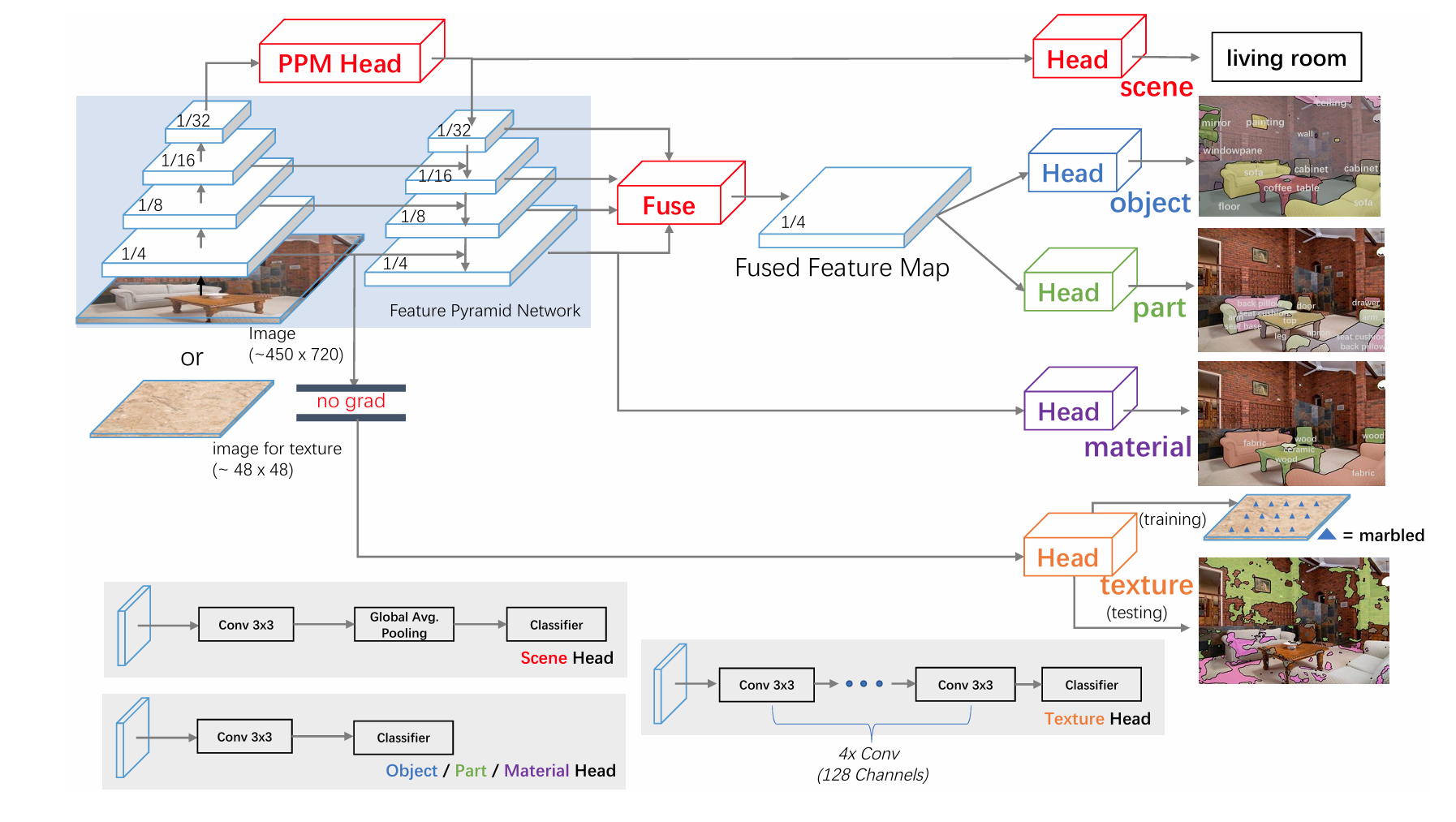
应用实例：UperNet 用于多任务学习

相关研究领域：迁移学习（Transfer Learning）：

​ 迁移学习（Transfer Learning, TL），分为 target task 和 source task，多任务学习对于每个任务之间都是平等对待的，而迁移学习是不平等的，迁移学习只关心在 target 任务上的性能。它的 performance 的前提假设：关联的二级任务可以主要为主要任务提供额外信息，可以提高主要任务的泛化程度（和多任务学习相同）

定义与概念：

• 领域（domain）：$\mathcal{D}=\{\mathcal{X}, p(x) \}$，由数据的特征空间和数据分布决定

• 任务（task）：$\mathcal{T}=\{\mathcal{Y}, f(\cdot) \}$，由标签空间 $\mathcal{Y}$ 和目标预测函数 $f(\cdot)$ 组成

迁移学习的定义是给定源域（source domain）$\mathcal{D}_s$ 和对应学次任务 $\mathcal{T}_s$ 的情况下，迁移到给定目标域（target domain）$\mathcal{D}_t$ 和对应学次任务 $\mathcal{T}_t$ 的学习任务，则 $\mathcal{D}_s \neq \mathcal{D}_t$ 或者 $\mathcal{T}_s \neq \mathcal{T}_t$，因此迁移学习可以分为：

• 数据域不同 $\mathcal{D}_s \neq \mathcal{D}_t$：
  • 数据分布不同 $P(\mathcal{X}_s) \neq P(\mathcal{X}_t)$ 不同，例如从 ImageNet pretrain 的 backbone 用于其他数据集
  • 数据空间不同 $\mathcal{X}_s \neq \mathcal{X}_t$，例子同上
• 任务不同 $\mathcal{T}_s \neq \mathcal{T}_t$
  • 预测标签不同 $\mathcal{Y}_s \neq \mathcal{Y}_t$，比如在 target task 上新增一个类别
  • 映射不同 $P_s(y|x) \neq P_t(y|x)$，例如同一个词在不同语境下有不同的含义

在线代深度学习 pretraining 时代，pretraining 都是在 source task 上的训练（大规模数据集上对模型进行初步训练），fine-tuning 或 downstream task training 就是在 target task 上的训练

迁移学习方法

同样类似于多任务学习，迁移学习可以用三种方式进行迁移：

• 实例迁移（Instance Transfer）：重新调整源域的实例权重用于目标域的数据
• 特征迁移（Feature Transfer）：将源域和目标域的特征映射到同一个共同空间中
• 参数迁移（Parameter Transfer）：根据源域和学习目标域模型的参数

实例迁移：领域自适应(domain adaptation)

​ 该方法适用于两个域之间的数据分布 overlap 较大的情况

问题设置：

​ 给定带有标签的源域数据 $\mathcal{D}s = {x{s_i}, y_{s_i}}{i=1}^{n_s} $，目标域数据 $\mathcal{D}T = {x{t_i}}{i=1}^{n_T} $（目标数据集上没有标签） 学习任务是学习出 $f_t$ 使得目标数据上的损失最小：

$$\min \sum_i \mathcal{L}(f_T(x_{t_i}), y_{t_i})$$

其中 $ y_{t_i} $ 是未知的（有点像 transductive 的 semi-supervised learning）

假设

• 相同的标签空间 $ \mathcal{Y}_s = \mathcal{Y}_t $
• 相同的依赖关系 $ p(y_s |x_s) = p(y_t|x_t)$
• （几乎）相同的特征空间 $ \mathcal{X}_s \simeq \mathcal{X}_t$
• 不同数据分布 $ p_s(x) \neq p_t(x) $

重要性采样

\begin{align} \theta^* =& \arg \min_{\theta} \mathbb{E}_{(x,y) \sim p_t} [\mathcal{L}(y, f_\theta(x))] \\ =& \arg \min_{\theta} \int_{(x,y)} p_t(x) \mathcal{L}(y, f_\theta(x)) dx \\ =& \arg \min_{\theta} \int_{(x,y)} p_s(x) \frac{p_t(x)}{p_s(x)} \mathcal{L}(y, f_\theta(x)) dx \\ =& \arg \min_{\theta} \mathbb{E}_{(x,y) \sim p_s} \left[ \frac{p_t(x)}{p_s(x)} \mathcal{L}(y, f_\theta(x)) \right] \end{align}

通过下式重新调整每个实例的权重：

$$\beta(x) = \frac{p_t(x)}{p_s(x)}$$

即我们需要在每个数据上估计两个域之间的概率比例，这里由两种处理方式：

• 先分别估计 $p_s(x)$ 和 $p_t(x)$，然后计算 $\beta(x)$，但是这样会面临着高方差的问题
• 更实用的解决方式是，直接估计 $\frac{p_t(x)}{p_s(x)}$（类似 diffusion 中学习的方式）

拒绝采样

​ 拒绝采样可以视作对重要性采样的一个量化版本，即重要性只可能为 0 和 1：

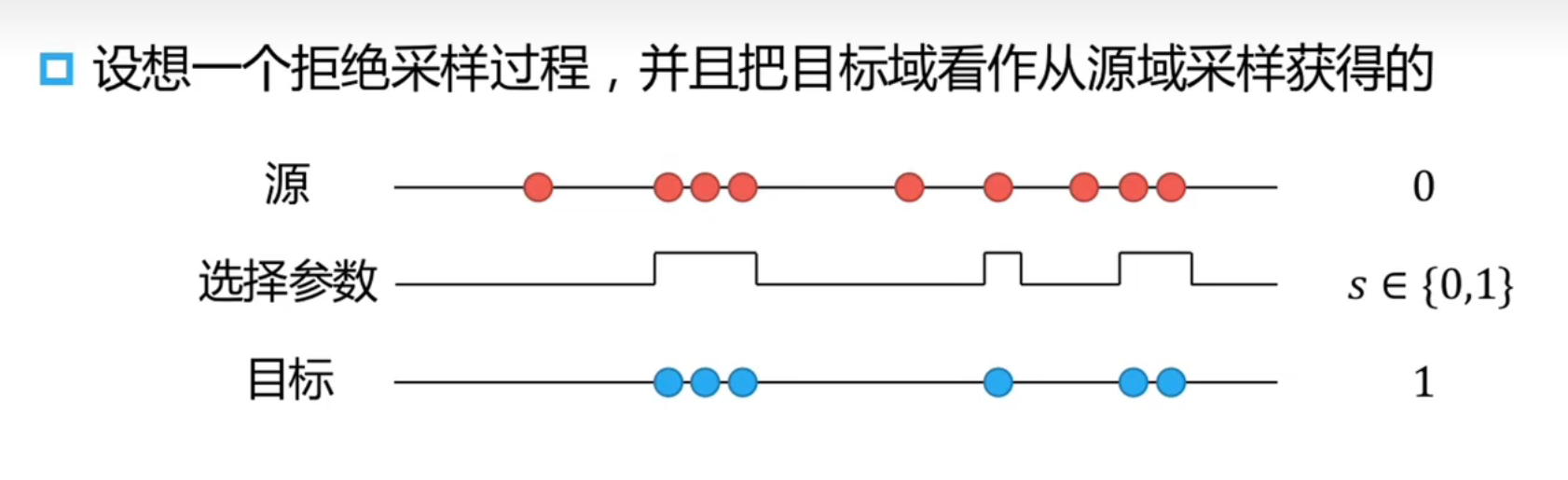
源域和目标域之间的关系为：

$$p_t(x) \propto p_s(x) p(s=1|x)$$

即把 $\beta(x)$ 视为一个而分类模型，可以用一个 logistic regression 的二分类器直接对数据进行分类

基函数估计

​ 仍然是机器学习的一个重要技巧，设置一些列的基函数，用基函数的线性加和去估计 $\beta(x)$：

$$\hat{\beta}(x) = \sum_{l=1}^b \alpha_l \phi_l(x)$$

特征迁移：

​ 当两个域之间数据分布 overlap 较小，这时候可以考虑用一个映射将两个数据分布拉进（在隐层中将两个域之间的特征分布进行拉进）

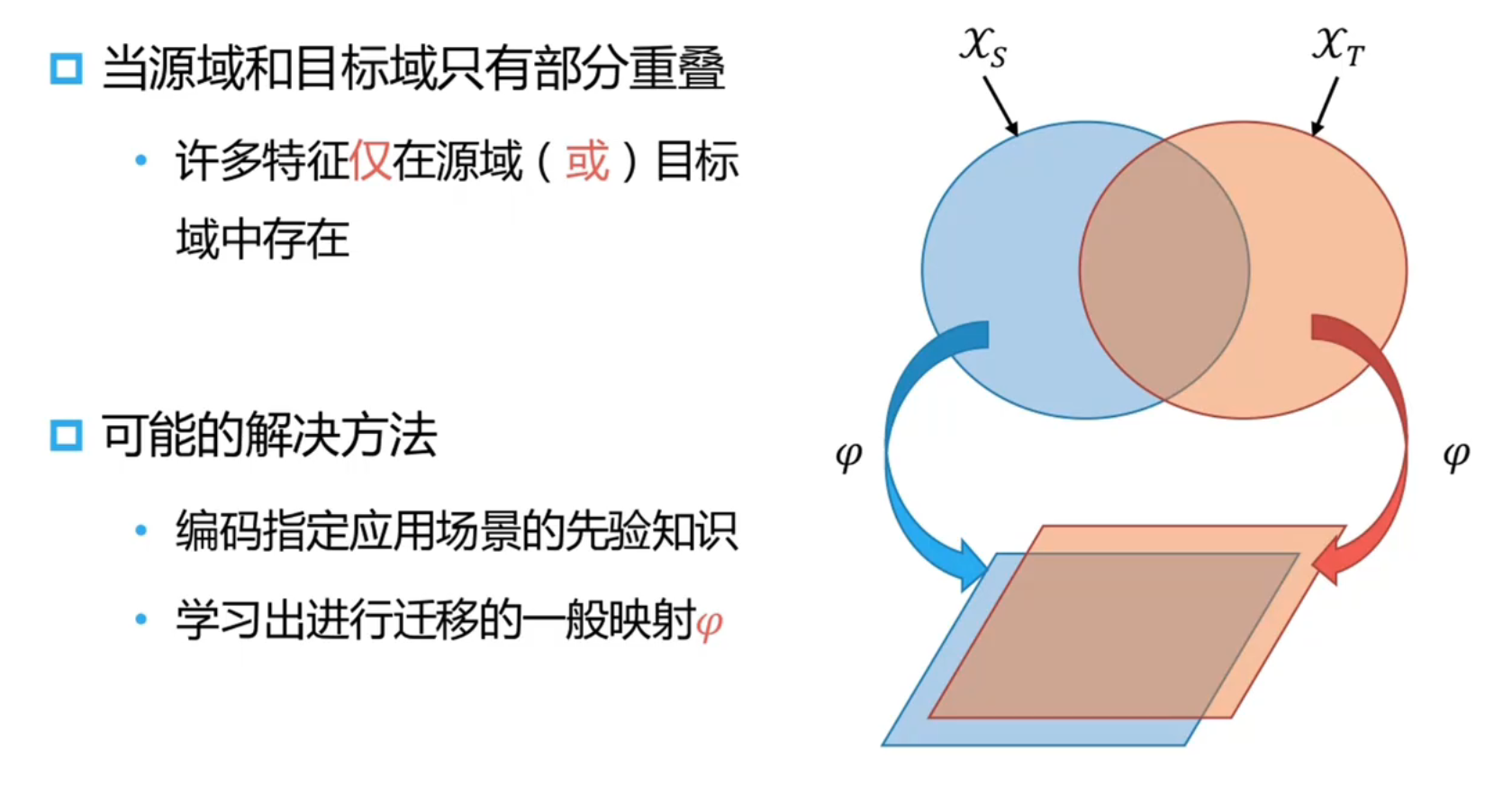
​ 学习的方式可以使用最小化两个领域分布之间的举例来学习新的数据表示，也可以使用多任务学习，自学习等方法

参数迁移：

​ 想法就是一个充分训练好的模型 $f_{\theta_s}(x)$ 已经学习到了源域的许多结构特征，如果两个参数是相关的，这一结构特征可以迁移到 target domain 的模型 $f_{\theta_t}$于是做法可以变为：最小化两个任务上的联合损失函数和模型参数之间的距离，先从两个域上学习的 $\theta$-参数化函数：

$$\theta_s^* = \arg \min_{\theta} \sum_{i=1}^{n_s} \mathcal{L}(y_{s_i}, f_\theta(x_{s_i})) + \lambda \Omega(\theta) \\ \theta_t^* = \arg \min_{\theta} \sum_{i=1}^{n_t} \mathcal{L}(y_{t_i}, f_\theta(x_{t_i})) + \lambda \Omega(\theta)$$

再在 target task 上进行训练：

$$\min_{\theta_s, \theta_t} \alpha \frac{1}{N_s} \sum_{i=1}^{N_s} \mathcal{L}(y_i, f_{\theta_s}(x_i)) + (1 - \alpha) \frac{1}{N_t} \sum_{j=1}^{N_t} \mathcal{L}(y_j, f_{\theta_t}(x_j)) + \lambda \Omega(\theta_s, \theta_t)$$

其中 $\alpha$ 的值可以随训练轮数增加而减小