拉格朗日凸优化

拉格朗日凸优化

​ 一般而言，非线性规划的问题有如下形式：

PA:{min⁡xf(x)subject to:hi(x)=0, i=1,2,⋯ ,mgj(x)≤0, j=1,2,⋯ ,lP_A: \begin{cases} \min_{\boldsymbol x} & f( \boldsymbol{x}) & \\ \text{subject to:} &h_i( \boldsymbol{x}) & = 0,\ i = 1,2,\cdots ,m \\ &g_j\left( \boldsymbol{x}\right) & \le 0,\ j = 1,2,\cdots ,l \end{cases}

其中自变量 x=(x1,x2,…,xn)T∈Rn\boldsymbol{x} = ( x_1,x_2,\dots ,x_n)^T \in \mathbb{R}^n，f(x)f( \boldsymbol{x}) 为目标函数，hi(x)=0(i=1,2,…,m)h_i( \boldsymbol{x}) = 0( i = 1,2,\dots ,m) 和 gj(x)≥0(j=1,2,⋯ ,l)g_j( \boldsymbol{x}) \ge 0( j = 1,2,\cdots ,l) 为约束条件。

​ 由于 max⁡f(x)=−min⁡(−f(x))\max f( \boldsymbol{x}) = - \min (-f(\boldsymbol{x}))，当需使目标函数极大化时只需使其负值极小化即
可。因而仅考虑目标函数极小化，这无损于一般性。若某约束条件是 ≤\le 不等式时，仅需在约束的两端同时取负号即可，因此这也无损一般性

无约束优化问题

定义拉格朗日函数 L(x,λ,μ)L(\boldsymbol x, \lambda, \mu) 如下：

L(x,λ,μ)=f(x)+λjgj(x)L(\boldsymbol x, \lambda, \mu) = f(\boldsymbol x) + \lambda_j g_j(\boldsymbol x)

则原优化问题等价于如下的优化问题：

PL:{min⁡xmax⁡λL(x,λ,μ)=f(x)+∑i=1mλigi(x)+∑j=1nμjhj(x)Subject to:λi≥0i=1,2,…,mP_L: \begin{cases} \min_{\boldsymbol x} \max_{\boldsymbol {\lambda}} &L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = f(\boldsymbol x) + \sum_{i=1}^m \lambda_i g_i(\boldsymbol{x}) + \sum_{j=1}^n \mu_j h_j(\boldsymbol{x}) \\ \text{Subject to:}& \lambda_i \geq 0 \quad i=1,2,\dots,m \end{cases}\\ \\

我们接下来说明优化问题 PLP_L 和优化问题 PAP_A 等价：

  • 若 x\boldsymbol x 在 PAP_A 的可行域之内，则对于 max⁡λ,μL(x,λ,μ)=f(x)+∑i=1mλigi(x)\max_{\boldsymbol {\lambda, \mu}} L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = f(\boldsymbol x) + \sum_{i=1}^m \lambda_i g_i(\boldsymbol{x}) 这个优化问题，x\boldsymbol x 为常值，后一项 ∑i=1mλigi(x)≤0\sum_{i=1}^m \lambda_i g_i(\boldsymbol{x}) \le 0，因此 max⁡λ,μL(x,λ,μ)=f(x)\max_{\boldsymbol {\lambda, \mu}} L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = f(\boldsymbol x)，经过外层的 min⁡\min 之后就等价于原问题

  • 若 x\boldsymbol x 在 PAP_A 的可行域之外，则至少存在一个存在 ii 使 gi(x)>0g_i(\boldsymbol x) > 0，代表着若取 λi→+∞\boldsymbol \lambda_i \rightarrow +\infty，其余 λj\boldsymbol \lambda_j 元素为零，则 max⁡λ,μL(x,λ,μ)=f(x)+∑i=1mλigi(x)\max_{\boldsymbol {\lambda, \mu}} L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = f(\boldsymbol x) + \sum_{i=1}^m \lambda_i g_i(\boldsymbol{x}) 这个优化问题的结果是 +∞+\infty，经过外层的 min⁡\min 后该项是一定被去掉的，即 PLP_L 等价于 PAP_A

对偶优化问题：

化为对偶问题的原因是，无论原问题是什么优化问题，对偶问题都是凸优化问题

PD:{max⁡λmin⁡xL(x,λ,μ)=f(x)+∑i=1mλigi(x)+∑j=1nμjhj(x)Subject to:λi≥0i=1,2,…,nP_D: \begin{cases} \max_{\boldsymbol {\lambda}} \min_{\boldsymbol x} &L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = f(\boldsymbol x) + \sum_{i=1}^m \lambda_i g_i(\boldsymbol{x}) + \sum_{j=1}^n \mu_j h_j(\boldsymbol{x}) \\ \text{Subject to:} & \lambda_i \geq 0 \quad i=1,2, \dots,n \end{cases} \\

下面推导原问题的最优解和对偶优化问题的最优解之间的关系，设原问题的最优解为 d∗d^*，对偶问题的最优解为 p∗p^*：

d∗=min⁡x∈Df(x)≥min⁡xf(x)d∗=max⁡λmin⁡x∈Df(x)≥max⁡λmin⁡xf(x)=p∗d^* = \min_{\boldsymbol x\in D}f(\boldsymbol x) \ge \min_{\boldsymbol x} f(\boldsymbol x)\\ d^* = \max_{\boldsymbol \lambda} \min_{\boldsymbol x\in D}f(\boldsymbol x) \ge \max_{\boldsymbol \lambda} \min_{\boldsymbol x} f(\boldsymbol x) = p^*

​ 这是一般化的原问题最优解和对偶问题最优解之间的关系，如果满足 Slater 条件和原问题是凸优化问题，则可以证明原问题和对偶问题最优解相同

步骤2：KKT条件

满足以下KKT条件时，点 x∗\boldsymbol x^* 为最优解：

  • 原问题可行条件：

hi(x∗)=0, i=1,2,...,mgj(x∗)≥0, j=1,2,...,nh_i(\boldsymbol x^*) = 0,\ i = 1,2,...,m\\ g_j(\boldsymbol x^*) \geq 0,\ j = 1,2,...,n

  • 对偶可行条件：

∇xL(x∗,λ∗,μ∗)=0μj≥0, j=1,2,...,l\nabla_x L(\boldsymbol x^*, \lambda^*, \mu^*) = 0 \\ \mu_j \geq 0,\ j = 1,2,...,l

  • 互补松弛性：

λjgj(x∗)=0, j=1,2,...,l\lambda_j g_j(\boldsymbol x^*) = 0,\ j = 1,2,...,l

在理解上唯一值得注意的就是互补松弛条件了，它的几何含义如下：

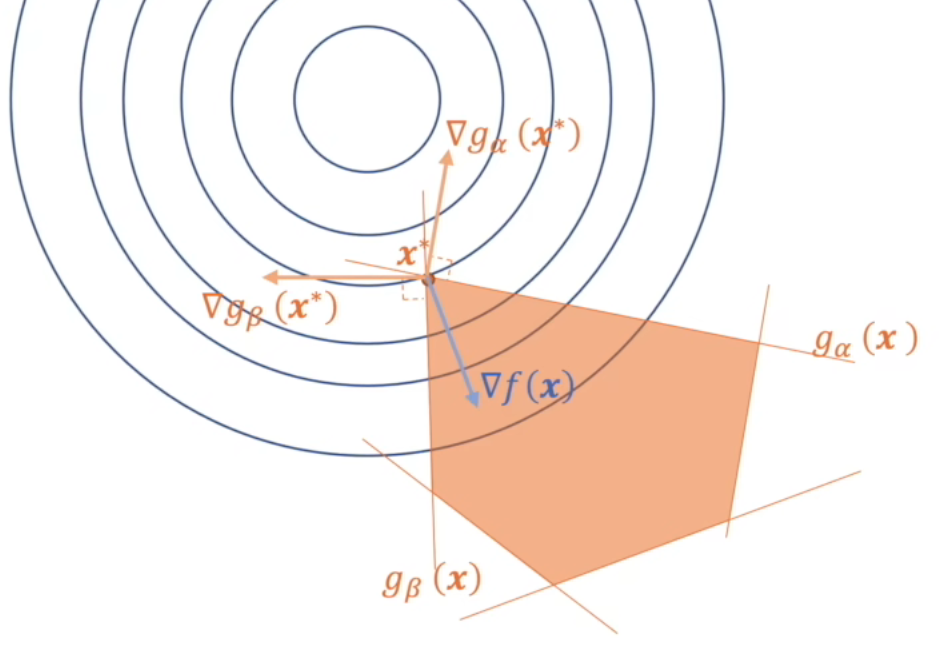
image-20250111164142193

  • 其中蓝色线为原问题 f(x)f(\boldsymbol x) 的等高线，gi(x)g_i(\boldsymbol x) 所围成的区域即为该优化问题的可行域，我们可以观察到不是所有的 gi(x)≤0g_i(\boldsymbol x) \le 0 都是对 x∗\boldsymbol x^* 发挥作用的，对于限制 x∗\boldsymbol x^* 的条件满足 gi(x)=0g_i(\boldsymbol x) = 0，而对于 gi(x)<0g_i(\boldsymbol x) < 0，由梯度条件 ∇λigi(x)=0\nabla \boldsymbol \lambda_i g_i(\boldsymbol x) =0，则可以推出互补松弛条件

​ 通过上述步骤，我们可以利用拉格朗日乘子法求解带有多元约束的优化问题。具体来说，我们通过构造拉格朗日函数并满足KKT条件来找到最优解。

对 $ \boldsymbol{x} $ 的偏导数

首先，计算 $ L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) $ 关于 $ \boldsymbol{x} $ 的偏导数：

∇xL(x,λ,μ)=∇f(x)+∑i=1mλi∇hi(x)+∑j=1lμj∇gj(x)\nabla_{\boldsymbol{x}} L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = \nabla f(\boldsymbol{x}) + \sum_{i=1}^m \lambda_i \nabla h_i(\boldsymbol{x}) + \sum_{j=1}^l \mu_j \nabla g_j(\boldsymbol{x})

将这个表达式设为零，得到：

∇f(x∗)+∑i=1mλi∗∇hi(x∗)+∑j=1lμj∗∇gj(x∗)=0\nabla f(\boldsymbol{x}^*) + \sum_{i=1}^m \lambda_i^* \nabla h_i(\boldsymbol{x}^*) + \sum_{j=1}^l \mu_j^* \nabla g_j(\boldsymbol{x}^*) = 0

这意味着对于每个分量 $ k $：

∂L(x∗,λ∗,μ∗)∂xk=∂f(x∗)∂xk+∑i=1mλi∗∂hi(x∗)∂xk+∑j=1lμj∗∂gj(x∗)∂xk=0\frac{\partial L(\boldsymbol{x}^*, \boldsymbol{\lambda}^*, \boldsymbol{\mu}^*)}{\partial x_k} = \frac{\partial f(\boldsymbol{x}^*)}{\partial x_k} + \sum_{i=1}^m \lambda_i^* \frac{\partial h_i(\boldsymbol{x}^*)}{\partial x_k} + \sum_{j=1}^l \mu_j^* \frac{\partial g_j(\boldsymbol{x}^*)}{\partial x_k} = 0

对 $ \boldsymbol{\lambda} $ 的偏导数

接下来，计算 $ L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) $ 关于 $ \boldsymbol{\lambda} $ 的偏导数：

∂L(x,λ,μ)∂λi=hi(x)\frac{\partial L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})}{\partial \lambda_i} = h_i(\boldsymbol{x})

将这个表达式设为零，得到原始可行性条件：

hi(x∗)=0, i=1,2,...,mh_i(\boldsymbol{x}^*) = 0,\ i = 1,2,...,m

对 $ \boldsymbol{\mu} $ 的偏导数

最后，计算 $ L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) $ 关于 $ \boldsymbol{\mu} $ 的偏导数：

∂L(x,λ,μ)∂μj=gj(x)\frac{\partial L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})}{\partial \mu_j} = g_j(\boldsymbol{x})

由于 $ \mu_j \geq 0 $ 并且 $ g_j(\boldsymbol{x}) \leq 0 $（因为 $ g_j(\boldsymbol{x}) \geq 0 $），我们有互补松弛性条件：

μjgj(x∗)=0, j=1,2,...,l\mu_j g_j(\boldsymbol{x}^*) = 0,\ j = 1,2,...,l

进一步理解和可视化

理解拉格朗日对偶条件：

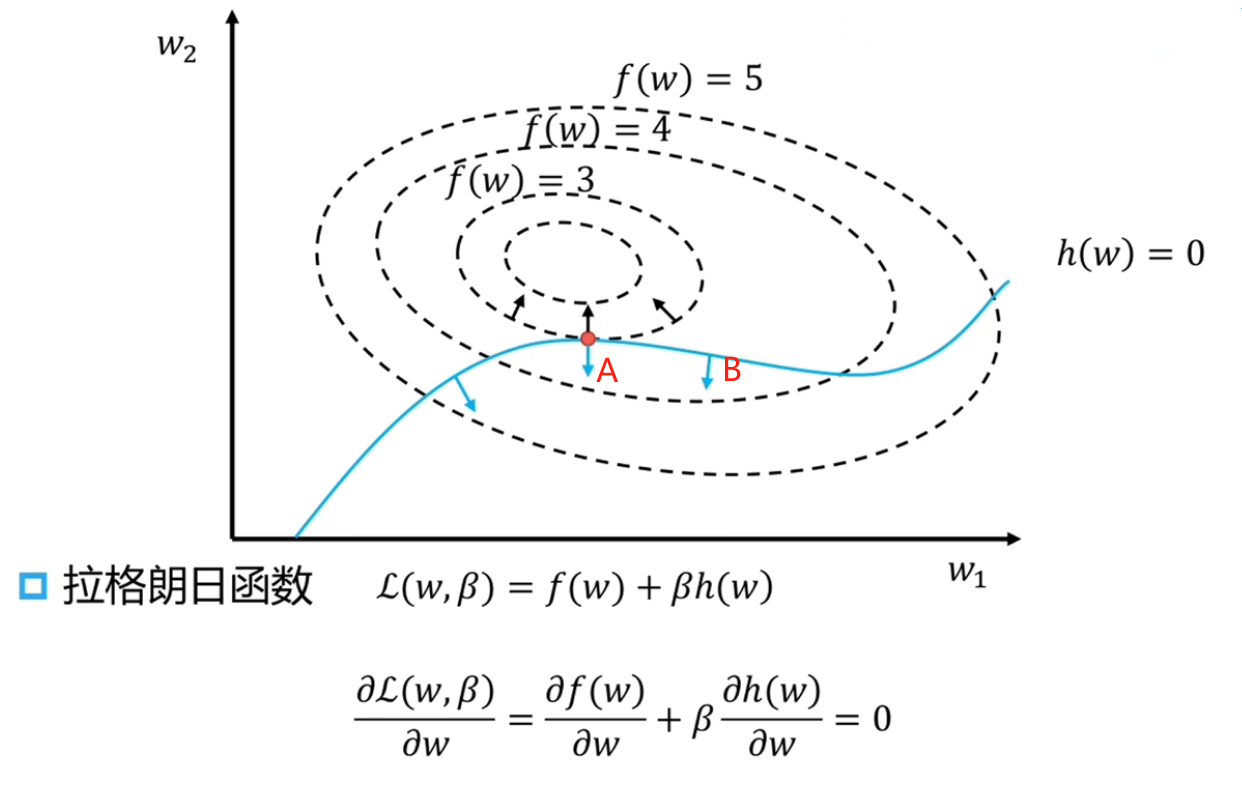
我们先考虑一种特殊情况：在 SVM 中，拉格朗日函数为：

L(w,β)=f(w)+βh(w)L(\boldsymbol w, \beta) = f(\boldsymbol w) + \beta h(\boldsymbol w)

则最优解的满足的条件为：

∂L(w,β)∂w=∂f(w)∂w+β∂h(w,β)∂β=0\frac{\partial L( {\boldsymbol w,\beta }) }{\partial \boldsymbol w} = \frac{\partial f(\boldsymbol w) }{\partial \boldsymbol w } + \beta \frac{\partial h(\boldsymbol w,\beta ) }{\partial \beta } = 0

​ 它的几何意义为：让 f(w)f(\boldsymbol w) 的等值曲面与约束条件 h(w)=0h(\boldsymbol w)=0 这条曲线相切，即 ∂f(w)∂w\frac{\partial f(\boldsymbol w) }{\partial \boldsymbol w } 和 ∂h(w)∂w\frac{\partial h(\boldsymbol w) }{\partial \boldsymbol w } 两梯度方向共线，对于有约束问题，它的可行域为 h(w)=0h(\boldsymbol w)=0，对可行域上的点 x0\boldsymbol x_0 进行微扰，假设在 x0\boldsymbol x_0 处存在一个方向和 ∂f(w)∂w\frac{\partial f(\boldsymbol w) }{\partial \boldsymbol w } 方向夹角为锐角，且和 ∂h(w)∂w\frac{\partial h(\boldsymbol w) }{\partial \boldsymbol w} 方向垂直，代表着我们可以沿着这个方向前进时可以让 f(w)f(\boldsymbol w) 减小的同时让 h(w)h(\boldsymbol w) 的值不变，即满足约束条件，因此极小值点处应满足的约束为 ∂f(w)∂w\frac{\partial f(\boldsymbol w) }{\partial \boldsymbol w } 和 ∂h(w)∂w\frac{\partial h(\boldsymbol w) }{\partial \boldsymbol w } 两梯度方向共线

  • 注意由于这个条件是充分条件，我们也可能解出极大值点

image-20250108093229625

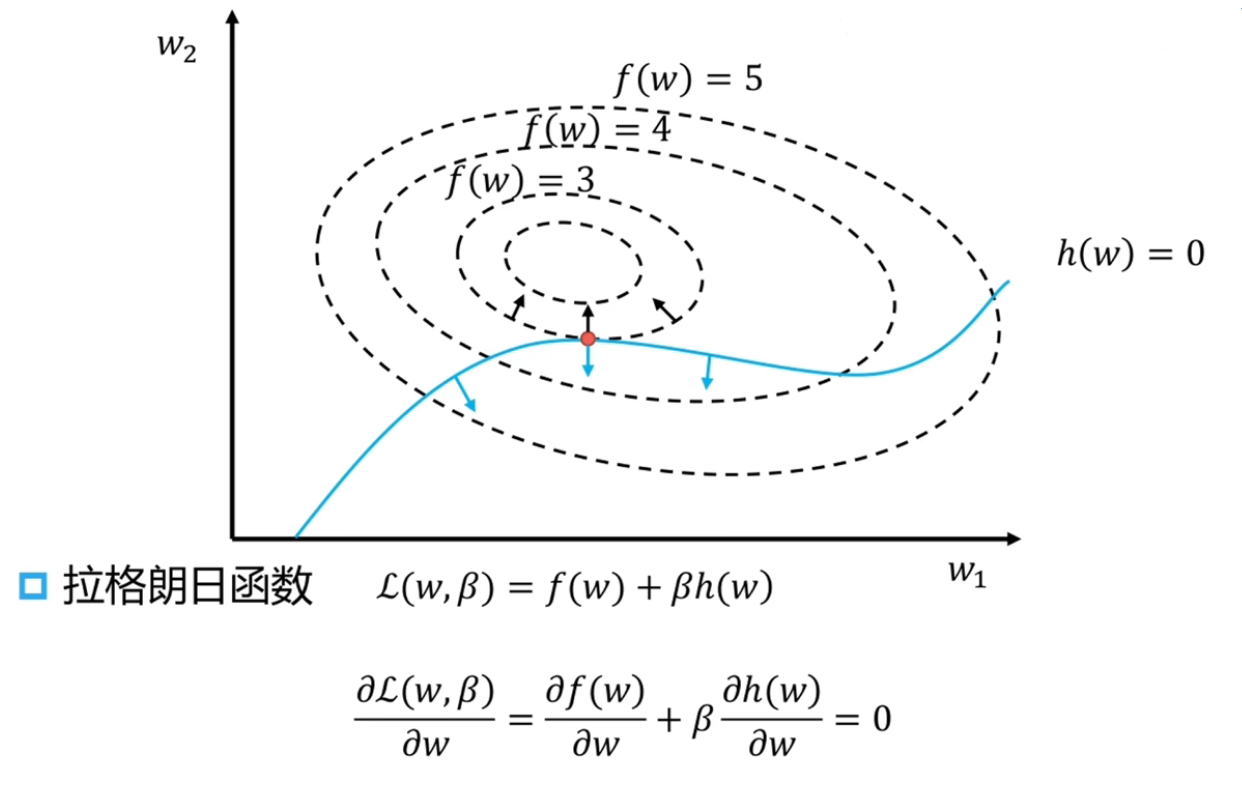
image-20250107195231081

我们再去理解 Lagrange 函数的构造过程，记下面方向 AA 为 h(w)h(\boldsymbol w) 增大的方向，那么构造的 Lagrange 函数 L(w,β)=f(w)+βh(w)L(\boldsymbol w, \beta) = f(\boldsymbol w) + \beta h(\boldsymbol w) 沿着方向 AA 就会让它的两个分量 f(w)f(\boldsymbol w) 和 h(w)h(\boldsymbol w) 同时增大，因此从这个角度来看，≥\ge 和 h(w)h(\boldsymbol w) 的增大方向是配对的（如果 h(w)h(\boldsymbol w) 沿 AA 的反方向增大，那这个极值问题本身是无意义或者 trivial 的，只能让拉格朗日乘子小于零这个问题才有意义），我们如果要让优化问题 PAP_A 到 PBP_B 的 +βh(w)+ \beta h(\boldsymbol w) 这个操作没有用的话，就让它加的正值部分在 f(w)f(\boldsymbol w) 的大值区域就行（非优解区域），这样就会迫使

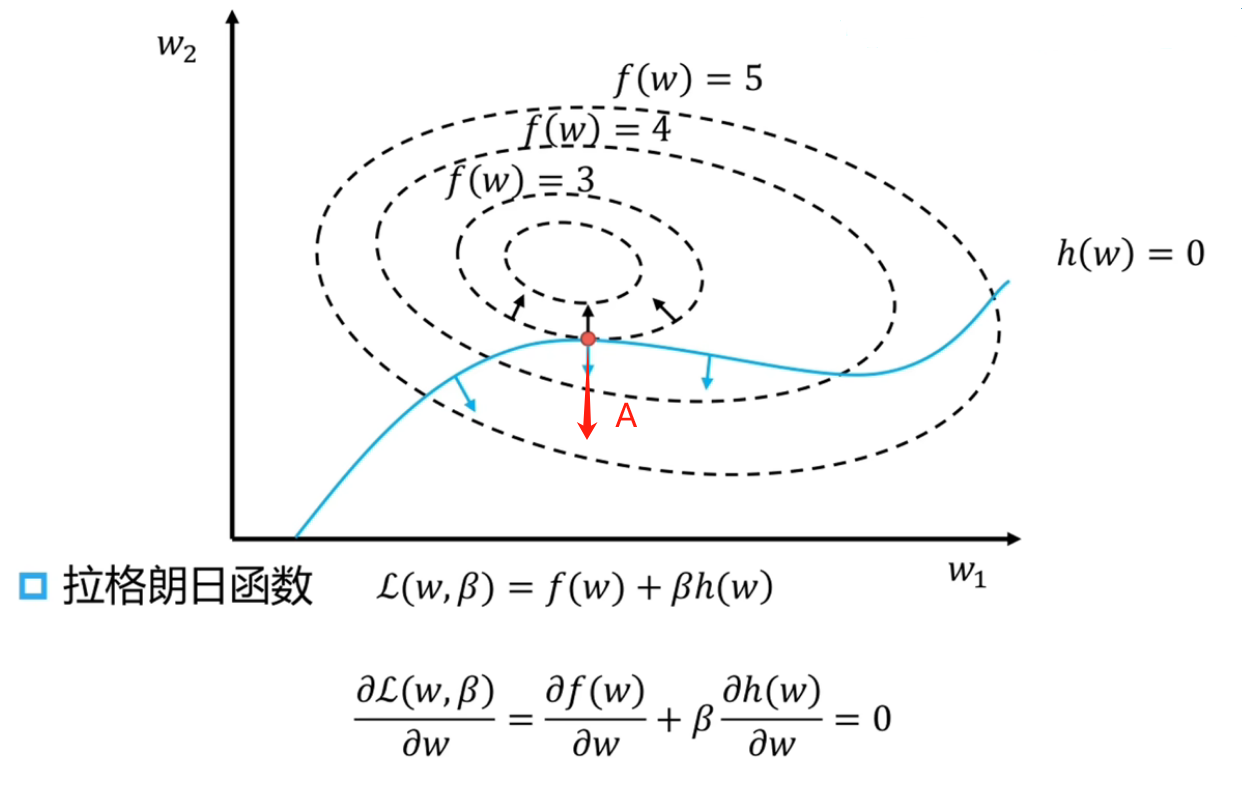
image-20250107200616524

拉格朗日对偶可视化

设原问题可行域为 DD，原问题表述如下：

PA:{min⁡xf(x)subject to:hi(x)=0, i=1,2,⋯ ,mgj(x)≤0, j=1,2,⋯ ,lP_A: \begin{cases} \min_{\boldsymbol x} & f( \boldsymbol{x}) & \\ \text{subject to:} &h_i( \boldsymbol{x}) & = 0,\ i = 1,2,\cdots ,m \\ &g_j\left( \boldsymbol{x}\right) & \le 0,\ j = 1,2,\cdots ,l \end{cases}

对偶问题：

PD:{max⁡λmin⁡xL(x,λ,μ)=f(x)+∑i=1mλigi(x)+∑j=1nμjhj(x)Subject to:λi≥0i=1,2,…,nP_D: \begin{cases} \max_{\boldsymbol {\lambda}} \min_{\boldsymbol x} &L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = f(\boldsymbol x) + \sum_{i=1}^m \lambda_i g_i(\boldsymbol{x}) + \sum_{j=1}^n \mu_j h_j(\boldsymbol{x}) \\ \text{Subject to:} & \lambda_i \geq 0 \quad i=1,2, \dots,n \end{cases} \\

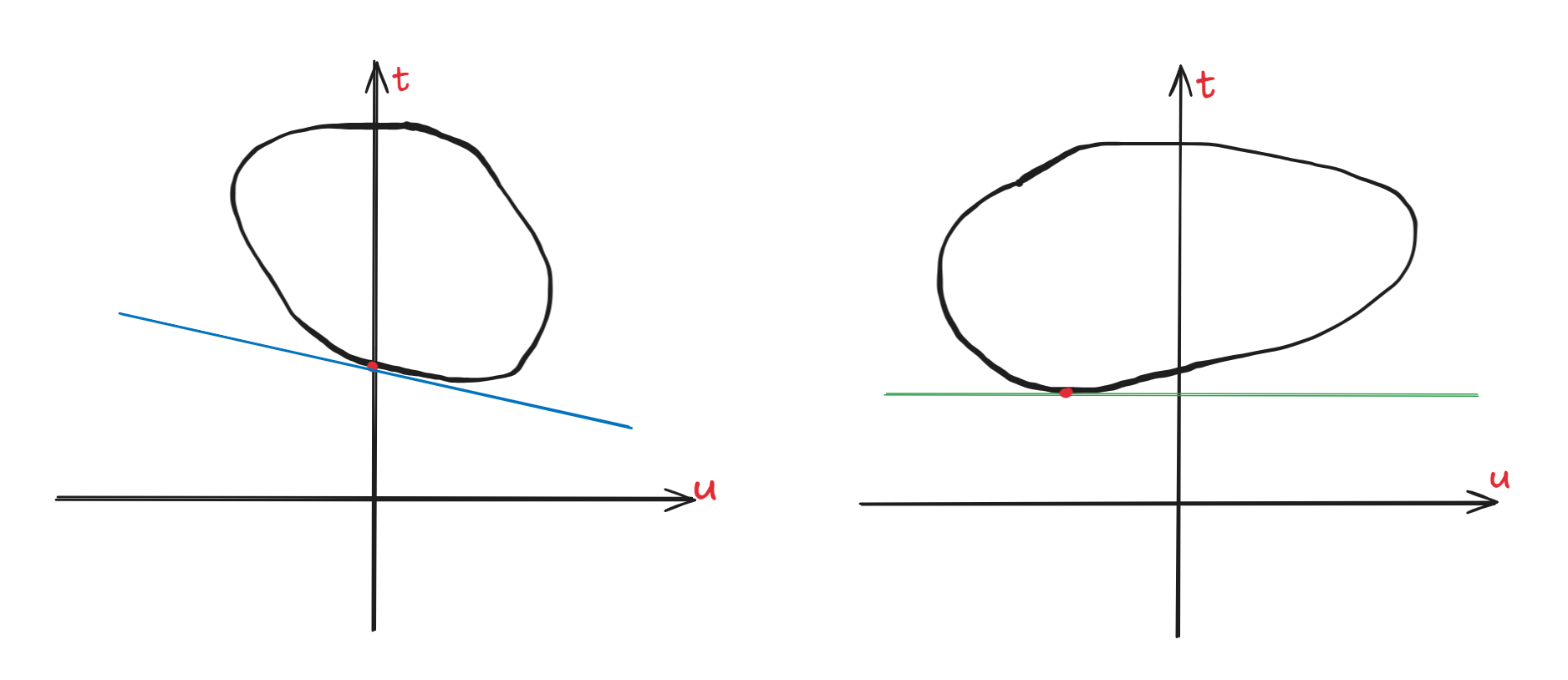
将拉格朗日函数写为：L(x,λ,μ)=t+ λTuL(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = t + \boldsymbol {\lambda^T u} ，为了可视化分析我们将 u\boldsymbol {u} 视为标量，即原问题和对偶问题的可行域为：

\begin{align} &G_1 = \{(t, \boldsymbol u)| t=f(\boldsymbol x), u_i= g_i(\boldsymbol x), \boldsymbol x \in D\} \\ &G_2 = \{(t, \boldsymbol u)| t=f(\boldsymbol x), u_i= g_i(\boldsymbol x), \boldsymbol x \in \mathbb{R}^n \} \end{align}

  • 这里可以看出 G1G_1 是 G2G_2 的子集，它们的核心区别在于 x∈D\boldsymbol x\in D，也就是 u≤0\boldsymbol {u}\le \boldsymbol 0，在后续的可视化的过程中我们可以看出区别

则原问题和对偶问题再改写形式：

Original problem: min⁡x{t∣(t,u)∈G1}Dual problem: max⁡λmin⁡x{t+ λTu∣(t,u)∈G2}\text{Original problem: } \min_\boldsymbol x \{t|(t, \boldsymbol u) \in G_1 \} \\ \text{Dual problem: } \max_\boldsymbol \lambda \min_\boldsymbol x\{t + \boldsymbol {\lambda^T u}|(t, \boldsymbol u) \in G_2 \}

可视化出 (t,u)(t, \boldsymbol u) 坐标系：

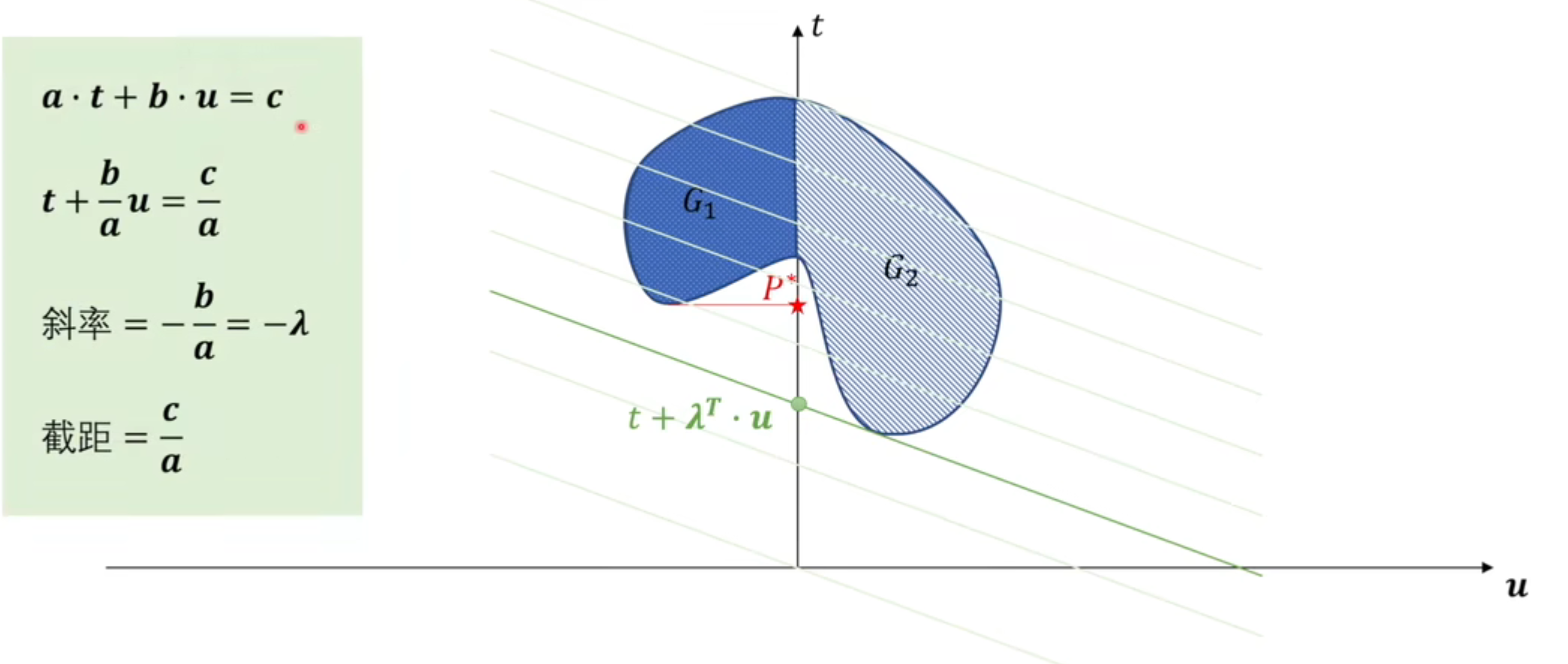
image-20250111153253727

  • 对于原问题的目标就是在 G1G_1 中寻找一个 tt 值最小的点，投影到 tt 轴上的值我们记为 P∗P^*，即为原问题的最优解
  • 对于对偶问题
    • 对于内层的 min⁡\min 优化：外层求 max⁡\max 的过程中的 λ\boldsymbol \lambda 为斜率，可以绘制一系列 t+λTut + \boldsymbol{\lambda}^T\boldsymbol u 的等值线，目标就是在 G2G_2 中寻找对应最小等值线的点，即等值线与 G2G_2 相切处的值
    • 对于外层的取最大值：求能够与可行域相切的等值线的斜率最大值，那么对于图中所示的最大值即为同时相切于两点的直线，则对于对偶问题的最终最优解就是该直线与 tt 轴的交点

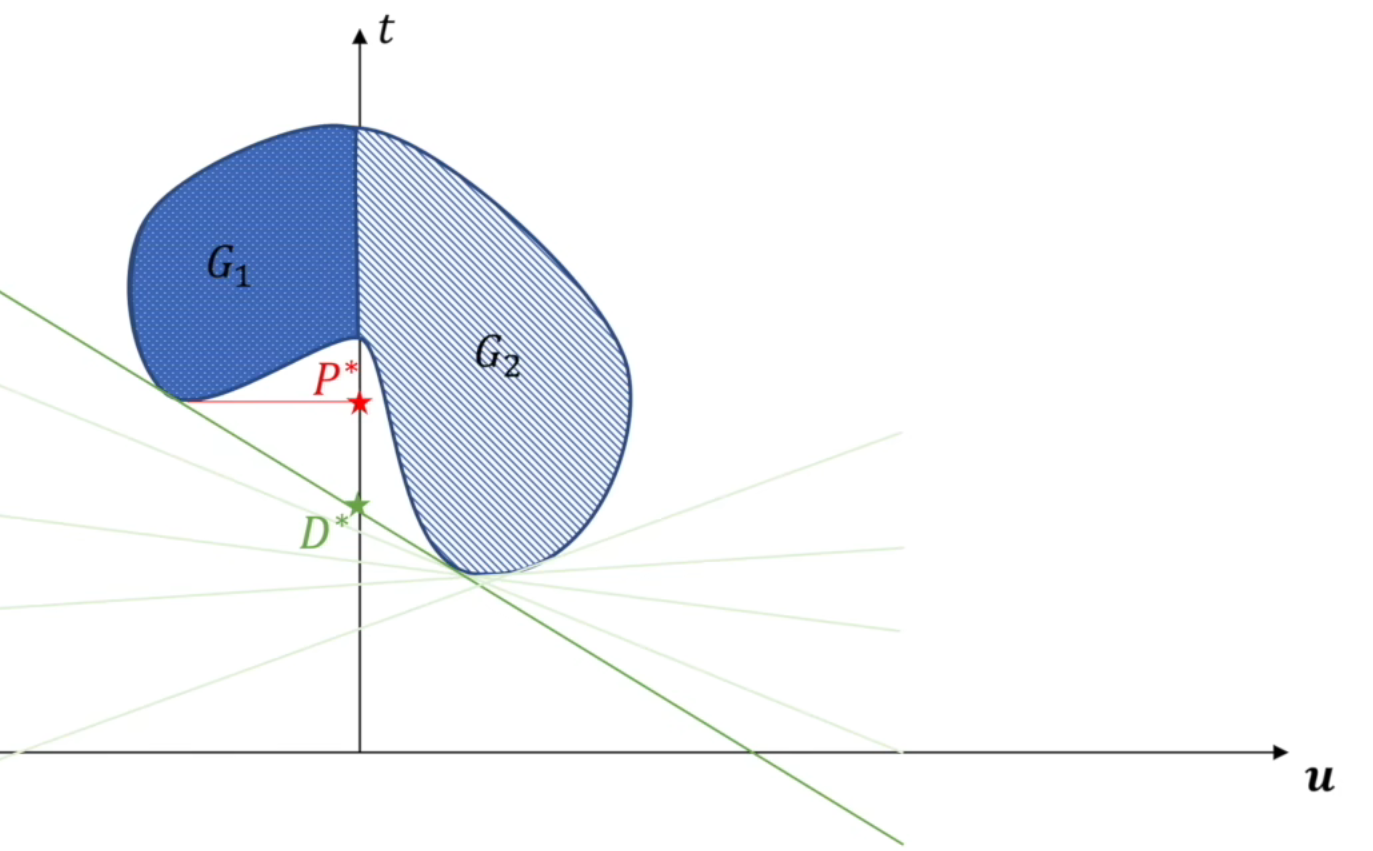
image-20250111155741428

​ 这张图也解释了弱对偶性，同时我们也可以用几何意义来解释 KKT 条件中的互补松弛条件：

在下面两种情况中，P∗P^* 和 Q∗Q^* 都是相同的，从下面这张图来看，对于绝大多数的凸优化问题，强对偶定理都成立，但是数学上仍然能够举例出特殊情况让他不成立，这就是 Slater 条件

image-20250111162928082