data_discri

数据降维

​ 数据降维是处理高维数据时常用的技术，它旨在减少数据集的特征数量同时尽可能保留原始数据的关键信息。常见的降维算法可以分为线性方法和非线性方法两大类，常见的线性降维算法有 PCA（Principal Component Analysis 无监督），LDA（Linear Discriminant Analysis 有监督）。非线性降维算法有 SNE（t-distributed Stochastic Neighbor Embedding 主要用于数据可视化），autoencoder 等

​ 这里指出数据降维并非一个特殊的概念。事实上，当我们将数据降维到单一维度时，这一过程实际上与寻找一个用于分类的拟合模型相类似。因此，从这个角度来看，数据降维可以被理解为构建一个简化模型的过程，该模型旨在捕捉数据的本质结构。

​ 在本篇文章中我们主要介绍线性降维方法 LDA 与 PCA

LDA：Fisher线性判别

​ Fisher 线性判别的目标是在保证类内方差最小化的同时最大化类间方差，即找到一个投影方向，使得投影后的数据点能够最大程度地分开不同的类别。考虑怎么建模这个投影，我们现考虑讲数据从

设数据集为 $\mathcal{D}=\{\boldsymbol{x}_1, \dots, \boldsymbol{x}_n\}$，其中每个数据点 $\boldsymbol{x}_i=(x_{i1}, x_{i2}, \dots, x_{id})^T$。再设数据服从分布 $\boldsymbol{x}_i \sim \boldsymbol{x}, \text{i.i.d}$，且数据被分为 $C$ 类，记作 $\mathcal{D}_1, \mathcal{D}_2, \dots, \mathcal{D}_C$。 我们的目标是找到一个投影向量 $\boldsymbol{w}$，使得数据在该轴上的投影能够最大化类间分离度，同时最小化类内离散度。这可以通过优化 Fisher 准则函数来实现：

定义类均值和总均值 对于每一类 $c$，我们定义其类均值 $\boldsymbol{\mu}_c$ 为：

$$\boldsymbol{\mu}_c = \frac{1}{N_c}\sum_{\boldsymbol{x}_i \in \mathcal{D}_c} \boldsymbol{x}_i,$$

其中 $N_c$ 是类别 $c$ 中的数据点数量。 定义总均值 $\boldsymbol{\mu}$ 为：

$$\boldsymbol{\mu} = \frac{1}{N}\sum_{i=1}^{n} \boldsymbol{x}_i,$$

其中 $N = \sum_{c=1}^{C} N_c$ 是所有数据点的总数。

2. 构建类内散度矩阵和类间散度矩阵 类内散度矩阵（within-class scatter matrix）$S_W$ 定义为：

我们先以二分类为例，我们建模目标函数 $J(\boldsymbol{w})$ 如下：我们考虑二分类问题，类别为 $y=1$ 和 $y=-1$。设投影向量为 $\boldsymbol{w}$，数据点 $\boldsymbol{x}_i$ 在该方向上的投影为 $s_i = \boldsymbol{w}^T \boldsymbol{x}_i$。

$$J(\boldsymbol{w}) = \frac{\text{between class scatter}}{\text{within class scatter}} = \frac{\left( \mathbb{E}[s|y=1] - \mathbb{E}[s|y=-1] \right)^2}{Var[s|y=1] + Var[s|y=-1]}$$

下面进一步化简均值和方差：

$$\mathbb{E}[s|y=i] = \mathbb{E}[\boldsymbol{w}^T\boldsymbol{x}|y=i] = \boldsymbol{w}^T\boldsymbol{\mu}_i \\ \left( \mathbb{E}[s|y=1] - \mathbb{E}[s|y=-1] \right)^2 = (\boldsymbol{w}^T\boldsymbol{\mu}_1 - \boldsymbol{w}^T\boldsymbol{\mu}_{-1})^2 = \boldsymbol{w}^T( \boldsymbol{\mu}_1- \boldsymbol{\mu}_{-1}) ( \boldsymbol{\mu}_1- \boldsymbol{\mu}_{-1})^T\boldsymbol{w} \\ Var[s|y=i] = \mathbb{E}[(s - \mathbb{E}[s|y=i])] = \mathbb{E}[(\boldsymbol{w}^T\boldsymbol{x} - \mathbb{E}[\boldsymbol{w}^T\boldsymbol{x}|y=i])^2] \\ =\mathbb{E}\left[\left(\boldsymbol{w}^T (\boldsymbol{x-\mu}_i )\right)^2 \right]=\boldsymbol{w}^T \mathbb{E}[(\boldsymbol{x-\mu}_c)(\boldsymbol{x-\mu}_c)^T] \boldsymbol{w} = \boldsymbol{w}^T \boldsymbol{\Sigma}_c \boldsymbol{w}$$

其中 $\boldsymbol{\Sigma}_c$ 为类别 $c$ 的协方差矩阵，则 $J(\boldsymbol{w})$ 可化为：

$$J(\boldsymbol{w}) = \frac{\left( \mathbb{E}[s|y=1] - \mathbb{E}[s|y=-1] \right)^2}{Var[s|y=1] + Var[s|y=-1]} = \frac{\boldsymbol{w}^T( \boldsymbol{\mu}_1- \boldsymbol{\mu}_{-1}) ( \boldsymbol{\mu}_1- \boldsymbol{\mu}_{-1})^T\boldsymbol{w}}{\boldsymbol{w}^T \boldsymbol{\Sigma}_1 \boldsymbol{w} + \boldsymbol{w}^T \boldsymbol{\Sigma}_{-1} \boldsymbol{w}}$$

定义类间散度矩阵 $\boldsymbol{S}_B$，类内散度矩阵 $\boldsymbol{S}_w$ 为（每个组数据 $\boldsymbol{S}_B,\boldsymbol{S}_w$ 都是定值）：

$$\boldsymbol{S}_B = ( \boldsymbol{\mu}_1- \boldsymbol{\mu}_{-1}) ( \boldsymbol{\mu}_1- \boldsymbol{\mu}_{-1})^T\\ \boldsymbol{S}_w = \boldsymbol{\Sigma}_1+\boldsymbol{\Sigma}_{-1}$$

则优化问题进一步转化：

$$J(\boldsymbol{w}) = \frac{\boldsymbol{w}^T\boldsymbol{S}_B\boldsymbol{w}}{\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}}$$

我们将 $\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}$ 固定，优化问题改为：

$$\boldsymbol{w} = \arg\max_w \boldsymbol{w}^T\boldsymbol{S}_B\boldsymbol{w} \\ \text{Subject to: }\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w} =K$$

使用拉格朗日乘子法：

$$L(\boldsymbol{w}, \lambda) = \boldsymbol{w}^T\boldsymbol{S}_B\boldsymbol{w} + \lambda (K-\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}) \\ =\boldsymbol{w}^T(\boldsymbol{S}_B -\lambda\boldsymbol{S}_w )\boldsymbol{w} + \lambda K \\ \frac{\partial L(\boldsymbol{w}, \lambda)}{ \partial \boldsymbol w}=\boldsymbol 0^T \Rightarrow 2(\boldsymbol{S}_B -\lambda\boldsymbol{S}_w )\boldsymbol{w} = \boldsymbol 0 \\\Rightarrow \boldsymbol{S}_B\boldsymbol w=\lambda \boldsymbol{S}_B\boldsymbol w$$

我们不关心 $w$ 的大小，我们只关系 $w$ 的方向，问题是该如何用 $w$ 的方向值去掉一个 $w$ 让我们接触一个方向？

$$\boldsymbol{S}_w^{-1}\boldsymbol{S}_B\boldsymbol w=\lambda \boldsymbol w \\ \Rightarrow\boldsymbol{S}_w^{-1} (\boldsymbol \mu_1 -\boldsymbol \mu _{-1})(\boldsymbol \mu_1 -\boldsymbol \mu _{-1})^T \boldsymbol w=\lambda \boldsymbol w \\ \Rightarrow\boldsymbol{S}_w^{-1} (\boldsymbol \mu_1 -\boldsymbol \mu _{-1})a=\lambda \boldsymbol w \\ \Rightarrow \boldsymbol w=\boldsymbol{S}_w^{-1} (\boldsymbol \mu_1 -\boldsymbol \mu _{-1})$$

• 考虑到 $\boldsymbol{S}_B$ 不可逆，因此我们对 $\boldsymbol S_w$ 取逆而非 $\boldsymbol S_B$（只有 $\boldsymbol{S}_w$ 可逆才能进行上面的推导）
• $(\boldsymbol \mu_1 -\boldsymbol \mu _{-1})^T \boldsymbol w=const$ 这一步挺有技巧性的，可以记一下
• 最后一步我们省去了 $\boldsymbol w$ 的模长，只关注了投影向量的方向

$$S_W = \sum_{c=1}^{C} \sum_{\boldsymbol{x}_i \in \mathcal{D}_c} (\boldsymbol{x}_i - \boldsymbol{\mu}_c)(\boldsymbol{x}_i - \boldsymbol{\mu}_c)^T.$$

类间散度矩阵（between-class scatter matrix）$S_B$ 定义为：

$$S_B = \sum_{c=1}^{C} N_c (\boldsymbol{\mu}_c - \boldsymbol{\mu})(\boldsymbol{\mu}_c -\boldsymbol{\mu})^T$$

Fisher准则函数 Fisher准则函数 $J(\boldsymbol{w})$ 定义为类间散度与类内散度的比例：

$$J(\boldsymbol{w}) = \frac{\boldsymbol{w}^T S_B \boldsymbol{w}}{\boldsymbol{w}^T S_W \boldsymbol{w}}$$

4. 最优化问题 为了最大化 Fisher 准则函数，我们需要解下列广义特征值问题：

$$S_B \boldsymbol{w} = \lambda S_W \boldsymbol{w},$$

其中 $\lambda$ 是广义特征值，$\boldsymbol{w}$ 是对应的广义特征向量。 通过求解上述方程，我们可以找到最优的投影方向 $\boldsymbol{w}$。在实际应用中，通常会将 $S_W$ 进行逆变换，然后将其转化为标准特征值问题进行求解：

$$(S_W^{-1} S_B) \boldsymbol{w} = \lambda \boldsymbol{w}.$$

最终，选择具有最大 $\lambda$ 值的特征向量作为最优的投影向量 $\boldsymbol{w}$，它对应于最大化 Fisher 准则函数的方向。

PCA：主成分分析

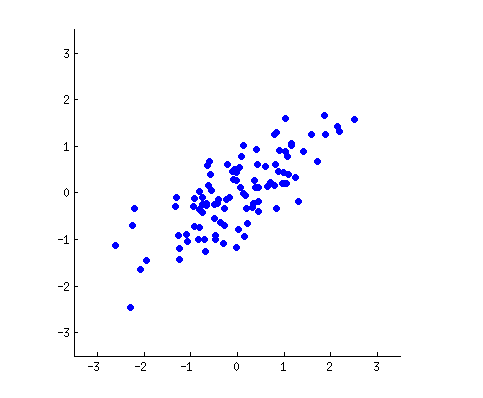
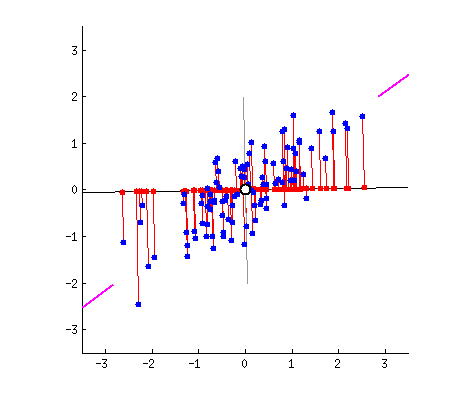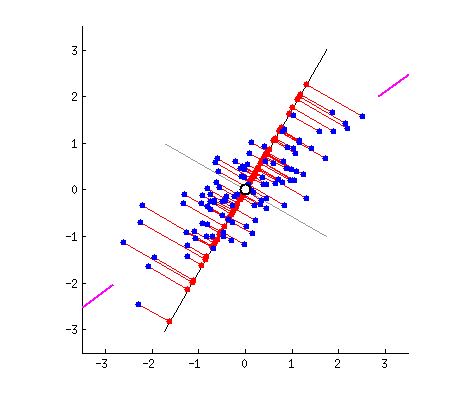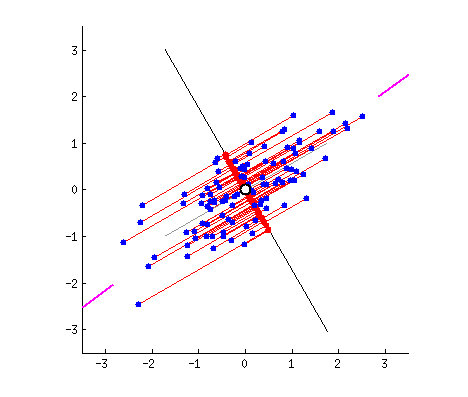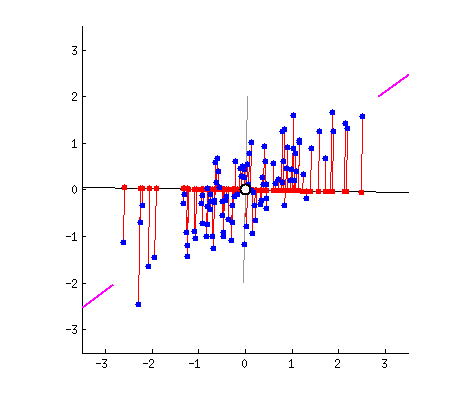
假设我们的数据分布如上图所示，我们想把数据的维度从二维降维到一维，我们尝试画一条线代表数据特征分布，那么我们可以感觉到“能将数据尽可能离散地分布到一个轴上，那个轴就是好的投影轴”，下面我们尝试去建模这个过程：

借助 logistic 回归的思想，我们想将对于删去的维度使数据尽可能集中，设数据为 $\mathcal{D}=\{\boldsymbol{x}_1, \dots, \boldsymbol{x}_n\}, \boldsymbol{x}_i=(x_{i1}, x_{i1}, \dots, x_{id})^T$ 代表我们的数据点，我们的目标就是找到一个轴使数据

我们将数据去中心化处理：

$$\boldsymbol{m} = \frac{1}{n}\sum_{i=1}^n \boldsymbol{x}_i \\ \text{Let } \tilde{\boldsymbol{x}_i}=\boldsymbol{x}_i-m \quad \tilde{\boldsymbol{X}} = [\tilde{\boldsymbol{x}_1}, \tilde{\boldsymbol{x}_2}, \dots, \tilde{\boldsymbol{x}_n}]^T$$

则数据的协方差为：

$$\Sigma = \frac{1}{n-1}\tilde{\boldsymbol{X}}\tilde{\boldsymbol{X}}^T$$

其中协方差矩阵除以除以 $n−1$ 而不是 $n$ 是为了获得无偏估计：

$$Cov(X, Y) = \frac{1}{n-1}\sum_{i=1}^n (x_i-x)(y_i-y)$$

后面我们都是对中心化之后的数据进行计算，所有的 $\boldsymbol{x}$ 默认为 $\tilde{\boldsymbol{x}}$

假如我们对数据进行正交变换：

$$\left\{ \begin{array}{l} \begin{matrix} z_1=l_{11}\tilde{x}_1+l_{12}\tilde{x}_2+\cdots l_{1d}\tilde{x}_d\\ z_2=l_{21}\tilde{x}_1+l_{22}\tilde{x}_2+\cdots l_{2d}\tilde{x}_d\\ \cdots \\ z_d=l_{d1}\tilde{x}_1+l_{d2}\tilde{x}_2+\cdots l_{dd}\tilde{x}_d \end{matrix}\\ \end{array} \right. \\ \boldsymbol{z} = \boldsymbol{Lx} \Rightarrow \boldsymbol{z}=\boldsymbol{Lx} \\$$

协方差矩阵的变化为：

$$\boldsymbol{\Lambda} = \frac{1}{n-1} \boldsymbol{z}\boldsymbol{z}^T = \frac{1}{n-1} \boldsymbol{Lxx}^T\boldsymbol{L}^T = \boldsymbol{L\Sigma L}^T$$

由 $\boldsymbol{\Sigma}$ 为一个实对称矩阵，假设其特征值均不相同，存在正交矩阵 $\boldsymbol{V}$ 使它能正交对角化：

$$\boldsymbol{\Sigma} = \boldsymbol{V \Lambda V}^T \\ \boldsymbol{\Lambda} = \text{diag}(\lambda _1,\lambda _2,\ldots ,\lambda_d)$$

其中 $\boldsymbol{V}=[\boldsymbol{v}_1,\boldsymbol{v}_2,\ldots ,\boldsymbol{v}_d]$，$\boldsymbol{v}_1,\boldsymbol{v}_2,\ldots ,\boldsymbol{v}_d$ 是 $\Sigma $ 的 $d$ 个单位长度的特征向量，$\lambda _1,\lambda _2,\ldots ,\lambda_d$ 是对应的特征值,那么我们可以写出

为什么我们要对协方差矩阵进行对角化？

当我们对协方差矩阵 $\Sigma$ 进行特征值分解对角化时，我们实际上是在寻找一组正交基(特征向量)，使得在这组基下，协方差矩阵除了对角元素以外的值都为零，即不同维度之间是不相关的；且对于对角元素的值，就是它对应所在方向上数据的方差：

现在考虑将原始数据投影到某一个特征向量 ${\boldsymbol{v}}_k$ 上。如果我们有一个中心化后的数据点 $\boldsymbol{x}$ ，它在 $\boldsymbol{v}_k$ 方向上的投影长度是 $\widetilde{\boldsymbol{x}}^T\boldsymbol{v}_k$ 。那么所有数据点在 $\boldsymbol{v}_k$ 方向上投影的方差可以表示为：

$$Var ({\boldsymbol{x}}^T\boldsymbol{v}_k) = \mathbb{E}\lbrack ({\boldsymbol{x}}^T \boldsymbol{v}_k)^2\rbrack - \lbrack \mathbb{E}({\boldsymbol{x}}^T\boldsymbol{v}_k)\rbrack^2$$

由于数据已经中心化,所以 $E(\boldsymbol{x}^T\boldsymbol{v}_k)= \mathbb{E}(\boldsymbol{x}^T)\boldsymbol{v}_k = 0$，因此上式简化为：

Var (\boldsymbol{x}^T \boldsymbol{v}_k) = \mathbb{E} ( \boldsymbol{x}^T \boldsymbol{v}_k)^2 = \mathbb{E} \left[ \boldsymbol{x}^T \boldsymbol{v}_k \boldsymbol{v}_k^T \boldsymbol{x} \right] \\ = \mathbb{E} \left[ \tr (\boldsymbol{x}^T \boldsymbol{v}_k \boldsymbol{v}_k^T \boldsymbol{x}) \right] = \mathbb{E} \left[ \tr (\boldsymbol{x}^T \boldsymbol{x}) \boldsymbol{v}_k \boldsymbol{v}_k^T \right] = \mathbb{E} \left[ \tr (\boldsymbol{x}^T \boldsymbol{x}) \right] \boldsymbol{v}_k \boldsymbol{v}_k^T \\ =\tr \left( \mathbb{E} \left[ \boldsymbol{x} \boldsymbol{x}^T \right] \boldsymbol{v}_k \boldsymbol{v}_k^T \right) = \tr \left( \Sigma \boldsymbol{v}_k \boldsymbol{v}_k^T \right) = \tr \left( \boldsymbol{v}_k^T \Sigma \boldsymbol{v}_k \right) = \boldsymbol{v}_k^T \Sigma \boldsymbol{v}_k

根据特征值分解的性质,我们知道 $\Sigma {\boldsymbol{v}}_k = {\lambda }_k{\boldsymbol{v}}_k$ ,因此：

$$Var (\boldsymbol{x}^T \boldsymbol{v}_k) = \boldsymbol{v}_k^T (\lambda _k \boldsymbol{v}_k) = \lambda_k(\boldsymbol{v}_k^T \boldsymbol{v}_k)$$

因为 ${\boldsymbol{v}}_k$ 是单位向量,所以 ${\boldsymbol{v}}_k^T{\boldsymbol{v}}_k = 1$ ,最终我们得到：

$$Var( {\boldsymbol{x}^T \boldsymbol{v}_k}) = \lambda_k$$

假设我们的数据分布如上图所示，我们希望将数据的维度从二维降到一维。为此，我们可以尝试画一条线来代表数据特征的分布。通过这条线，我们可以直观地感受到“能将数据尽可能离散地分布在某个轴上，这个轴就是良好的投影轴”。接下来，我们将建模这一过程。

借鉴逻辑回归的思想，我们希望通过保留一个轴使数据尽可能集中。设数据集为 $\mathcal{D}=\{\boldsymbol{x}_1, \dots, \boldsymbol{x}_n\}$，其中每个数据点 $\boldsymbol{x}_i=(x_{i1}, x_{i2}, \dots, x_{id})^T$。再设数据服从分布 $\boldsymbol{x}_i \sim \boldsymbol{x}, \text{i.i.d}$ 我们的目标是找到这样一个轴，使得数据在该轴上的投影能够最大化数据的分散程度。

首先，我们需要对数据进行中心化处理：

$$\boldsymbol{m} = \frac{1}{n}\sum_{i=1}^n \boldsymbol{x}_i \\ \text{令 } \tilde{\boldsymbol{x}_i}=\boldsymbol{x}_i-\boldsymbol{m} \quad \tilde{\boldsymbol{X}} = [\tilde{\boldsymbol{x}_1}, \tilde{\boldsymbol{x}_2}, \dots, \tilde{\boldsymbol{x}_n}]^T$$

此时，数据的协方差矩阵为：

$$\Sigma = \frac{1}{n-1}\tilde{\boldsymbol{X}}\tilde{\boldsymbol{X}}^T$$

这里，协方差矩阵除以 $n-1$ 而不是 $n$ 是为了获得无偏估计：

$$Cov(X, Y) = \frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})$$

后续的所有计算都将基于中心化后的数据，因此默认情况下所有 $\boldsymbol{x}$ 均指代 $\tilde{\boldsymbol{x}}$。接下来，如果我们对数据进行正交变换：

$$\left\{ \begin{array}{l} \begin{matrix} z_1=l_{11}\tilde{x}_1+l_{12}\tilde{x}_2+\cdots l_{1d}\tilde{x}_d\\ z_2=l_{21}\tilde{x}_1+l_{22}\tilde{x}_2+\cdots l_{2d}\tilde{x}_d\\ \cdots \\ z_d=l_{d1}\tilde{x}_1+l_{d2}\tilde{x}_2+\cdots l_{dd}\tilde{x}_d \end{matrix}\\ \end{array} \right. \\ \boldsymbol{z} = \boldsymbol{Lx}$$

则协方差矩阵的变化为：

$$\boldsymbol{\Lambda} = \frac{1}{n-1} \boldsymbol{z}\boldsymbol{z}^T = \frac{1}{n-1} \boldsymbol{Lxx}^T\boldsymbol{L}^T = \boldsymbol{L\Sigma L}^T$$

由于 $\boldsymbol{\Sigma}$ 是一个实对称矩阵，假设其特征值互不相同，则存在正交矩阵 $\boldsymbol{V}$ 使其能够正交对角化：

$$\boldsymbol{\Sigma} = \boldsymbol{V \Lambda V}^T \\ \boldsymbol{\Lambda} = \text{diag}(\lambda _1,\lambda _2,\ldots ,\lambda_d)$$

其中 $\boldsymbol{V}=[\boldsymbol{v}_1,\boldsymbol{v}_2,\ldots ,\boldsymbol{v}_d]$，$\boldsymbol{v}_1,\boldsymbol{v}_2,\ldots ,\boldsymbol{v}_d$ 是 $\boldsymbol{\Sigma} $ 的 $d$ 个单位长度的特征向量，而 $\lambda _1,\lambda _2,\ldots ,\lambda_d$ 则是对应的特征值。

那么，为什么要对协方差矩阵进行对角化呢？

当我们对协方差矩阵 $\Sigma$ 进行特征值分解时，实际上是在寻找一组正交基（即特征向量），使得在这组基下，协方差矩阵除了对角元素外均为零，这意味着不同维度间相互独立；同时，这些对角元素正是对应方向上数据的方差。

现在考虑将原始数据投影到某一特定特征向量 ${\boldsymbol{v}}_k$ 上。对于一个已中心化的数据点 $\boldsymbol{x}$，它在 ${\boldsymbol{v}}_k$ 方向上的投影长度为 $\widetilde{\boldsymbol{x}}^T{\boldsymbol{v}}_k$。因此，所有数据点在 ${\boldsymbol{v}}_k$ 方向上投影的方差可以表示为：

$$Var ({\boldsymbol{x}}^T{\boldsymbol{v}}_k) = \mathbb{E}\lbrack ({\boldsymbol{x}}^T {\boldsymbol{v}}_k)^2\rbrack - \lbrack \mathbb{E}({\boldsymbol{x}}^T{\boldsymbol{v}}_k)\rbrack^2$$

由于数据已经进行了中心化处理，故有 $\mathbb{E}(\boldsymbol{x}^T{\boldsymbol{v}}_k)= \mathbb{E}(\boldsymbol{x}^T){\boldsymbol{v}}_k = 0$，于是上述公式简化为：

Var (\boldsymbol{x}^T {\boldsymbol{v}}_k) = \mathbb{E} ( \boldsymbol{x}^T {\boldsymbol{v}}_k)^2 = \mathbb{E} \left[ \boldsymbol{x}^T {\boldsymbol{v}}_k {\boldsymbol{v}}_k^T \boldsymbol{x} \right] \\ = \mathbb{E} \left[ \tr (\boldsymbol{x}^T {\boldsymbol{v}}_k {\boldsymbol{v}}_k^T \boldsymbol{x}) \right] = \mathbb{E} \left[ \tr (\boldsymbol{x}^T \boldsymbol{x}) {\boldsymbol{v}}_k {\boldsymbol{v}}_k^T \right] = \mathbb{E} \left[ \tr (\boldsymbol{x}^T \boldsymbol{x}) \right] {\boldsymbol{v}}_k {\boldsymbol{v}}_k^T \\ =\tr \left( \mathbb{E} \left[ \boldsymbol{x} \boldsymbol{x}^T \right] {\boldsymbol{v}}_k {\boldsymbol{v}}_k^T \right) = \tr \left( \Sigma {\boldsymbol{v}}_k {\boldsymbol{v}}_k^T \right) = \tr \left( {\boldsymbol{v}}_k^T \Sigma {\boldsymbol{v}}_k \right) = {\boldsymbol{v}}_k^T \Sigma {\boldsymbol{v}}_k

根据特征值分解的性质，我们知道 $\Sigma {\boldsymbol{v}}_k = {\lambda }_k{\boldsymbol{v}}_k$，因此：

$$Var (\boldsymbol{x}^T {\boldsymbol{v}}_k) = {\boldsymbol{v}}_k^T (\lambda _k {\boldsymbol{v}}_k) = \lambda_k({\boldsymbol{v}}_k^T {\boldsymbol{v}}_k)$$

又因为 ${\boldsymbol{v}}_k$ 是单位向量，所以 ${\boldsymbol{v}}_k^T{\boldsymbol{v}}_k = 1$，最终得到：

$$Var( {\boldsymbol{x}^T {\boldsymbol{v}}_k}) = \lambda_k$$