这篇文章是为了总结矩阵求导和反向传播推导的,
求导布局包括:分子布局或分母布局。
分子布局:求导结果的维度以分子为主。分子是列向量形式,分母是行向量形式,例如:
∂ f 2 × 1 ( x ) ∂ x 3 × 1 T = [ ∂ f 1 ∂ x 1 ∂ f 1 ∂ x 2 ∂ f 1 ∂ x 3 ∂ f 2 ∂ x 1 ∂ f 1 ∂ x 2 ∂ f 2 ∂ x 3 ] 2 × 3 \frac{\partial {\boldsymbol{f}}_{2 \times 1}( \boldsymbol{x}) }{\partial \boldsymbol{x}_{3 \times 1}^T} =
{\left\lbrack \begin{array}{lll}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} &
\frac{\partial f_1}{\partial x_3} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \frac{\partial f_2}{\partial x_3} \end{array}\right\rbrack }_{2 \times 3}
∂ x 3 × 1 T ∂ f 2 × 1 ( x ) = [ ∂ x 1 ∂ f 1 ∂ x 1 ∂ f 2 ∂ x 2 ∂ f 1 ∂ x 2 ∂ f 1 ∂ x 3 ∂ f 1 ∂ x 3 ∂ f 2 ] 2 × 3
分母布局:求导结果的维度以分母为主。分子是行向量形式,分母是列向量形式
∂ f 2 × 1 T ( x ) ∂ x 3 × 1 = [ ∂ f 1 ∂ x 1 ∂ f 2 ∂ x 1 ∂ f 1 ∂ x 2 ∂ f 2 ∂ x 2 ∂ f 1 ∂ x 3 ∂ f 2 ∂ x 3 ] 3 × 2 \frac{\partial {\boldsymbol{f}}_{2 \times 1}^{T}\left( \boldsymbol{x}\right) }{\partial {\boldsymbol{x}}_{3 \times 1}} =
{\left\lbrack \begin{array}{ll}
\frac{\partial f_1}{\partial {x}_1} & \frac{\partial f_2}{\partial {x}_1}\\
\frac{\partial f_1}{\partial {x}_2} & \frac{\partial f_2}{\partial {x}_2}\\
\frac{\partial f_1}{\partial {x}_3} & \frac{\partial f_2}{\partial {x}_3} \end{array}\right\rbrack }_{3 \times 2}
∂ x 3 × 1 ∂ f 2 × 1 T ( x ) = ⎣ ⎢ ⎢ ⎡ ∂ x 1 ∂ f 1 ∂ x 2 ∂ f 1 ∂ x 3 ∂ f 1 ∂ x 1 ∂ f 2 ∂ x 2 ∂ f 2 ∂ x 3 ∂ f 2 ⎦ ⎥ ⎥ ⎤ 3 × 2
对于一个 n n n Y \boldsymbol{Y} Y m m m X \boldsymbol{X} X n + m n+m n + m y i y_i y i x j x_j x j ∂ y i x j \frac{\partial y_i}{x_j} x j ∂ y i
从严格的数学定义来看, y \boldsymbol{y} y W \boldsymbol{W} W y \boldsymbol{y} y m m m W \boldsymbol{W} W m × n m \times n m × n m × m × n m \times m \times n m × m × n L L L W \boldsymbol{W} W ∂ L ∂ W \frac{\partial L}{\partial \boldsymbol{W}} ∂ W ∂ L
∂ L ∂ W = ∑ i = 1 m ∂ L ∂ y i ∂ y i ∂ W \frac{\partial L}{\partial \boldsymbol{W}} = \sum_{i = 1}^m\frac{\partial L}{\partial y_i}\frac{\partial y_i}{\partial \boldsymbol{W}}
∂ W ∂ L = i = 1 ∑ m ∂ y i ∂ L ∂ W ∂ y i
其中 ∂ L ∂ y i \frac{\partial L}{\partial y_i} ∂ y i ∂ L ∂ y i ∂ W \frac{\partial y_i}{\partial \boldsymbol{W}} ∂ W ∂ y i m × n m \times n m × n y i y_i y i W i j W_{ij} W i j y = W x + b \boldsymbol{y} = \boldsymbol{W}\boldsymbol{x} + \boldsymbol{b} y = W x + b
y i = ∑ k = 1 n W i k x k + b i ⇒ ∂ y i ∂ W j k = x k δ i j = { x k if i = j 0 else y_i = \sum_{k=1}^n W_{ik} x_k + b_i \\
\Rightarrow \frac{\partial y_i}{\partial W_{jk}} = x_k\delta_{ij} =
\left\{ \begin{array}{l}
x_k \quad \text{if } i=j\\
0 \quad \text{else}\\
\end{array} \right.
y i = k = 1 ∑ n W i k x k + b i ⇒ ∂ W j k ∂ y i = x k δ i j = { x k if i = j 0 else
这意味着在实际计算中,∂ y i ∂ W \frac{\partial y_i}{\partial \boldsymbol{W}} ∂ W ∂ y i i i i i i i
∂ y i ∂ W j k = x k δ i j ⇒ ∂ L ∂ W j k = ∑ i = 1 m ∂ L ∂ y i ∂ y i ∂ W j k = ∂ L ∂ y i x k \frac{\partial y_i}{\partial W_{jk}} = x_k\delta_{ij} \\
\Rightarrow \frac{\partial L}{\partial W_{jk}} = \sum_{i = 1}^m \frac{\partial L}{\partial y_i}\frac{\partial y_i}{\partial W_{jk}} = \frac{\partial L}{\partial y_i}x_k
∂ W j k ∂ y i = x k δ i j ⇒ ∂ W j k ∂ L = i = 1 ∑ m ∂ y i ∂ L ∂ W j k ∂ y i = ∂ y i ∂ L x k
观察 ∂ L ∂ W j k \frac{\partial L}{\partial W_{jk}} ∂ W j k ∂ L j j j k k k ∂ L ∂ y , x \frac{\partial L}{\partial \boldsymbol{y}}, \boldsymbol{x} ∂ y ∂ L , x
∂ L ∂ W = ∂ L ∂ y x T \frac{\partial L}{\partial \boldsymbol{W}} = \frac{\partial L}{\partial \boldsymbol{y}}\boldsymbol{x}^T
∂ W ∂ L = ∂ y ∂ L x T
从此出可以看出梯度矩阵的秩是很低的,意味着在某些情况下,模型中可能存在冗余参数。同时低秩梯度矩阵可能会导致优化过程中的平坦区域(plateaus),使得梯度下降算法收敛速度变慢。这是因为当梯度矩阵接近低秩时,Hessian矩阵(二阶导数矩阵)可能会变得病态(ill-conditioned)
由于低秩矩阵的特殊结构,可以在不损失太多精度的情况下对它们进行近似处理,比如通过奇异值分解(SVD)保留主要成分。可以用来加速训练过程
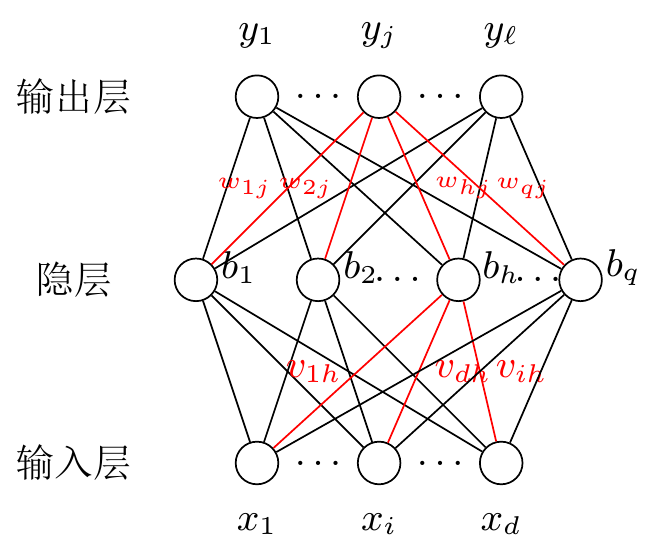
记上面的输入层的输入为 x \boldsymbol{x} x f f f b \boldsymbol{b} b
b = f ( V x + b 0 ) y = W b + b 1 \boldsymbol{b} = f(\boldsymbol{Vx} + \boldsymbol{b}_0) \\
\boldsymbol{y} = \boldsymbol{Wb} + \boldsymbol{b}_1 \\
b = f ( V x + b 0 ) y = W b + b 1
其中 b 0 , b 1 \boldsymbol{b}_0, \boldsymbol{b}_1 b 0 , b 1
einsum 我们思考为什么上面的标量 y i y_i y i W \boldsymbol{W} W ∂ y i ∂ W \frac{\partial y_i}{\partial \boldsymbol{W}} ∂ W ∂ y i
下面我们去推导更加一般的结论,由于矩阵乘法是 einsum 的一种特例,我们直接对 einsum 总结一般性规律。我们定义基础算子为:对某一维度进行对应元素相乘并求和 ,那么矩阵乘法就是进行广播-基础算子-转置的结果,那么如果 einsum 对 2 2 2
1 2 'b i j k, j k -> b i' , A, B)
那么虽然 C \boldsymbol{C} C A , B \boldsymbol{A,B} A , B 6 , 4 6,4 6 , 4 A \boldsymbol{A} A A \boldsymbol{A} A 因此计算 A \boldsymbol{A} A 2 2 2 :
∂ L ∂ A b i j k = ∑ b i ( ∂ L ∂ C b i ∂ C b i ∂ A b i j k ) C b i = ∑ j k A b i j k B j k ⇒ ∂ L ∂ A b i j k = ∂ L ∂ C b i ⋅ B j k \frac{\partial L}{\partial \boldsymbol{A}_{bijk}} = \sum_{bi}\left( \frac{\partial L}{\partial \boldsymbol{C}_{bi}}\frac{\partial \boldsymbol{C}_{bi}}{\partial \boldsymbol{A}_{bijk}}\right) \\
\boldsymbol{C}_{bi} = \sum_{jk} \boldsymbol{A}_{bijk}\boldsymbol{B}_{jk} \\
\Rightarrow \frac{\partial L}{\partial \boldsymbol{A}_{bijk}} = \ \frac{\partial L}{\partial \boldsymbol{C}_{bi}} \cdot \boldsymbol{B}_{jk}
∂ A b i j k ∂ L = b i ∑ ( ∂ C b i ∂ L ∂ A b i j k ∂ C b i ) C b i = j k ∑ A b i j k B j k ⇒ ∂ A b i j k ∂ L = ∂ C b i ∂ L ⋅ B j k
因此可以推出 A \boldsymbol{A} A
1 dL_dA = torch.einsum('b i, j k' , dL_dC, B)
记法说明:记上面的输入层的输入为 x \boldsymbol{x} x f f f b \boldsymbol{b} b
b = f ( V x + b 0 ) y = W b + b 1 \boldsymbol{b} = f(\boldsymbol{Vx} + \boldsymbol{b}_0) \\
\boldsymbol{y} = \boldsymbol{Wb} + \boldsymbol{b}_1 \\
b = f ( V x + b 0 ) y = W b + b 1
其中 b 0 , b 1 \boldsymbol{b}_0, \boldsymbol{b}_1 b 0 , b 1
损失函数对 W \boldsymbol{W} W
∂ L ∂ W = ∂ L ∂ y ∂ y ∂ W = ∂ L ∂ y b T \frac{\partial L}{\partial \boldsymbol{W}} = \frac{\partial L}{\partial \boldsymbol{y}}\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{W}} = \frac{\partial L}{\partial \boldsymbol{y}}\boldsymbol{b}^T
∂ W ∂ L = ∂ y ∂ L ∂ W ∂ y = ∂ y ∂ L b T
损失函数对 b 1 {\boldsymbol{b}}_1 b 1
∂ L ∂ b 1 = ∂ L ∂ y ∂ y ∂ b 1 = ∂ L ∂ y \frac{\partial L}{\partial \boldsymbol{b}_1} = \frac{\partial L}{\partial \boldsymbol{y}}\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{b}_1} = \frac{\partial L}{\partial \boldsymbol{y}}
∂ b 1 ∂ L = ∂ y ∂ L ∂ b 1 ∂ y = ∂ y ∂ L
对于输入层到隐藏层的连接 ( V 和 b 0 ) \left( {\boldsymbol{V}\text{ 和 }{\boldsymbol{b}}_0}\right) ( V 和 b 0 ) b \boldsymbol{b} b
∂ L ∂ b = ∂ L ∂ y ∂ y ∂ b = W T ∂ L ∂ y \frac{\partial L}{\partial \boldsymbol{b}} = \frac{\partial L}{\partial \boldsymbol{y}}\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{b}} = {\boldsymbol{W}}^T\frac{\partial L}{\partial \boldsymbol{y}}
∂ b ∂ L = ∂ y ∂ L ∂ b ∂ y = W T ∂ y ∂ L
现在我们可以计算 V \boldsymbol{V} V b 0 {\boldsymbol{b}}_0 b 0 f f f
∂ L ∂ ( V x + b 0 ) = ∂ L ∂ b ⊙ f ′ ( V x + b 0 ) \frac{\partial L}{\partial \left( {\boldsymbol{V}\boldsymbol{x} + {\boldsymbol{b}}_0}\right) } = \frac{\partial L}{\partial \boldsymbol{b}} \odot {f}^{\prime }( {\boldsymbol{V}\boldsymbol{x} + {\boldsymbol{b}}_0})
∂ ( V x + b 0 ) ∂ L = ∂ b ∂ L ⊙ f ′ ( V x + b 0 )
○ 损失函数对 V \boldsymbol{V} V
∂ L ∂ V = ( ∂ L ∂ b ⊙ f ′ ( V x + b 0 ) ) x T \frac{\partial L}{\partial \boldsymbol{V}} = \left( {\frac{\partial L}{\partial \boldsymbol{b}} \odot {f}^{\prime }\left( {\boldsymbol{V}\boldsymbol{x} + {\boldsymbol{b}}_0}\right) }\right) {\boldsymbol{x}}^T
∂ V ∂ L = ( ∂ b ∂ L ⊙ f ′ ( V x + b 0 ) ) x T
损失函数对 b 0 {\boldsymbol{b}}_0 b 0
∂ L ∂ b 0 = ∂ L ∂ b ⊙ f ′ ( V x + b 0 ) \frac{\partial L}{\partial {\boldsymbol{b}}_0} = \frac{\partial L}{\partial \boldsymbol{b}} \odot {f}^{\prime }\left( {\boldsymbol{V}\boldsymbol{x} + {\boldsymbol{b}}_0}\right)
∂ b 0 ∂ L = ∂ b ∂ L ⊙ f ′ ( V x + b 0 )