bayes_opt

贝叶斯优化

intro

​ 贝叶斯优化是一种针对评估成本高昂的黑箱函数进行优化的技术，广泛应用于机器学习超参数调整、实验设计和全局优化问题中。其核心在于利用概率模型（如高斯过程）构建目标函数的代理模型，并通过迭代更新此模型以选择最有可能提供改进的点进行评估，从而逐步逼近全局最优解

​ 对于如下形式的优化问题：

$$\max_{\boldsymbol{x} \in \mathcal{X}}f(\boldsymbol{x})$$

其中各参数的含义如下：

• 优化函数 $f$ ：$f: \mathbb{R}^d \rightarrow \mathbb{R}$ 为一个黑盒函数（模型），即我们不能先验地知道 $f$ 的各种性质，例如凸性，线性
• 搜索空间 $\mathcal{X}$：向量 $x \in \mathbb{R}^d$ 的搜索空间（优化空间）

​ 贝叶斯优化极其适合以下场景：

• 决策变量 $\boldsymbol{x}$ 的维度 $d\le 20$
• $f$ 的观测代价很高（$f$ is expensive to evaluate），不然我们更好的方式去优化这个目标。观测代价大有两点含义：
  • 每次计算 $f$ 的某一观测值时候代价很大，例如比较大的神经网络
  • 每次观测 $f$ 的时候需要花费成本，这个花费是对于观测这个动作而言的，例如
• $f$ 是一个黑盒模型（函数），我们不知道 $f$ 的解析式，也不知道 $f$ 的一阶导数或者二阶导数
• 观测值可能存在噪声，但假设为独立同分布，具有零均值和恒定方差

因此，贝叶斯优化非常适合于神经网络等复杂模型的超参数优化任务

贝叶斯优化

模拟退火 vs 贝叶斯优化

​ 在介绍贝叶斯优化之前，我们先介绍一下模拟退火算法，模拟退火算法基于物理退火过程，通过逐渐降低“温度”参数来控制搜索空间的探索范围，允许算法跳出局部最优解。每次迭代中，根据一定概率接受新解，即使该解比当前解更差，这个概率随温度下降而减小。：

Simulated Annealing:

Initialize with random $x$

for some restriction:

​ sample a step $\Delta x \sim P(x)$

​ if $f(x + \Delta x) \ge f(x)$:

​ with some acceptance probability $x \leftarrow x + \Delta x$

​ else:

​ $x \leftarrow x + \Delta x$

​ 模拟退火算法可以理解为就是没有代理模型进行启发搜索的贝叶斯算法，即模拟退火算法和贝叶斯算法之间就相差了一个代理模型来引导下一步的搜索过程

适用场景

• 模拟退火：适用于离散或连续但不规则的空间，尤其是问题规模大、解空间复杂的情况，不需要关于目标函数的先验知识（也是适用黑盒模型）
• 贝叶斯优化：适合评估成本高昂的黑箱函数优化，例如机器学习超参数调优，因为其能高效利用每一步的信息更新代理模型（但是解空间的维度不能太高）

特性	模拟退火	贝叶斯优化
优点	- 不依赖梯度 - 能逃离局部极值	- 较少评估次数取得好结果 - 自适应调整搜索策略
局限性	- 需要调整冷却时间表 - 高维问题收敛慢	- 主要适用于低到中等维度 - 构建和更新代理模型有计算成本

代理模型 (Surrogate Model)

​ 我们使用一个概率模型 $p({f|\boldsymbol{x},D})$ 来表示目标函数 $f$ 的分布,其中 $D = \{ ( \boldsymbol{x}_i,y_i) \}_{i = 1}^n$ 是已经观察到的数据集，$\boldsymbol{x}_i$ 是输入点，而 $y_i = f( \boldsymbol{x}_i) + \epsilon$ 是带噪声的观测值,这里 $\epsilon$ 是均值为 $0$、方差为 $\sigma_n^2$ 的高斯噪声。常见的代理概率模型是一个高斯过程(Gaussian Process, GP)，它假设函数值 $f( \boldsymbol{x})$ 在不同的输入点之间是联合正态分布的,可以写作：

$$f( \boldsymbol{x}) \sim \mathcal{GP}\left( \mu_\boldsymbol{x},k\left( \boldsymbol{x},{\boldsymbol{x}}^\prime\right) \right)$$

给定数据 $D$ 后,根据贝叶斯定理更新后的后验分布为：

$$p(y_\ast|\boldsymbol{x}_{ \ast },D) = \mathcal{N}(\mu_{\boldsymbol{x}_ *},\sigma_{\boldsymbol{x}_*}^2)$$

这里的 $y_*$ 是新输入点 $\boldsymbol{x}_*$ 处的观测值, $\mu_{\boldsymbol{x}_*}$ 和 $\sigma_{\boldsymbol{x}_*}^2$，分别是其预测均值和方差。当噪声水平较低或已知时，我们可以将 $y$ 的预测均值 $\mu_{\boldsymbol{x}_*}$ 视为 $f(\boldsymbol{x}_*)$ 的近似估计

采集函数 (Acquisition Function)

​ 贝叶斯优化的核心问题是：基于现有的已知情况，如果选择下一步评估的数据点？在主动学习中我们选择不确定性最大的点，但在贝叶斯优化中我们需要在探索不确定性区域（探索）和关注已知具有较优目标值的区域之间进行权衡（开发）。这种评价的依据称之为采集函数（Acquisition Functions），采集函数通过当前模型启发式的评估是否选择一个数据点（类似强化学习的 explore & exploit）

​ 为了决定下一个要评估的点 $\boldsymbol{x}_{n + 1}$ ,我们定义一个采集函数 $a( {\boldsymbol{x};D})$ ,它衡量了选择 $\boldsymbol{x}$ 作为下一个评估点的价值。常用的采集函数包括 Probability of Improvement (PI) 和 Expected Improvement (EI)：

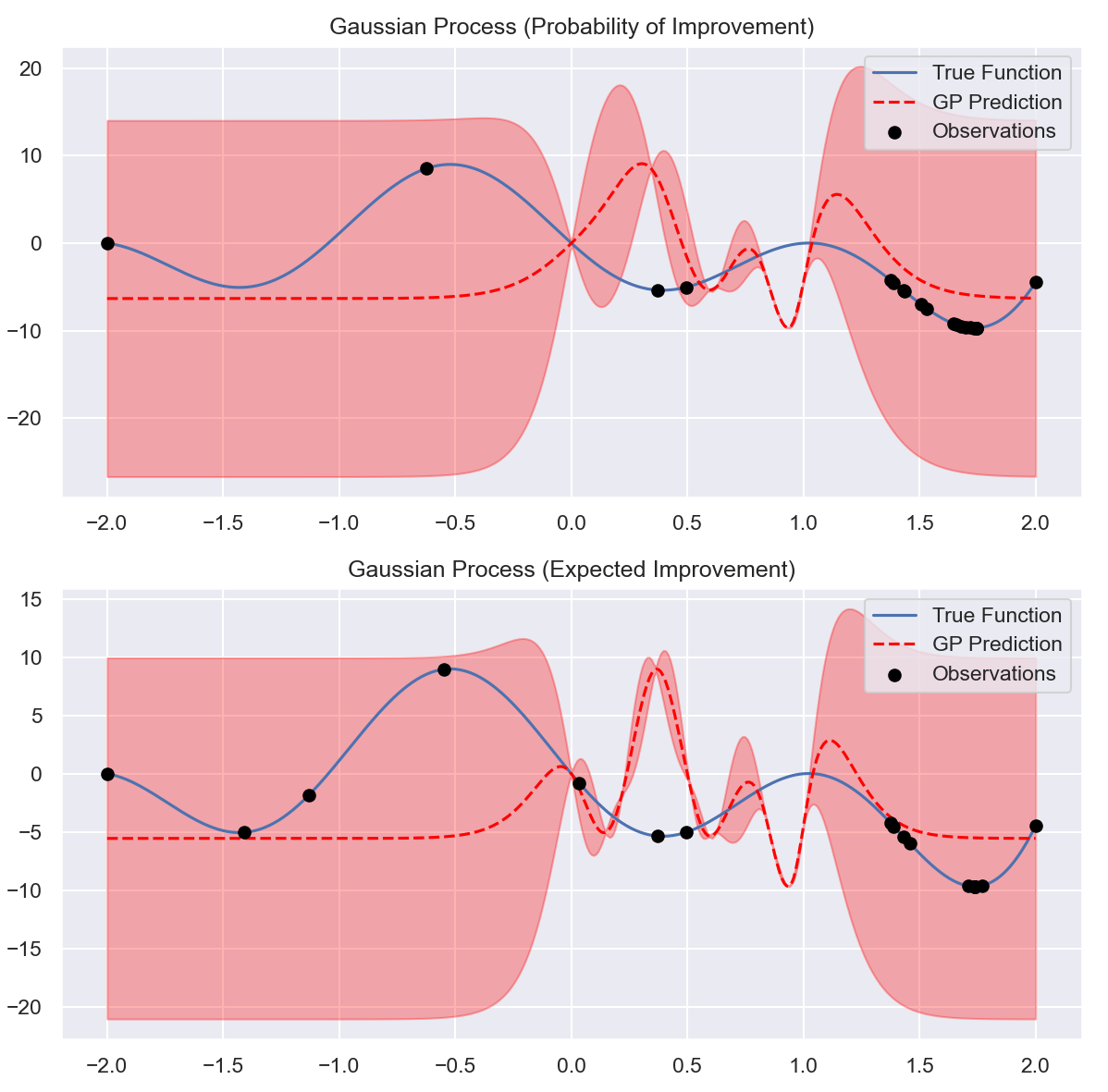
Probability of Improvement (PI)

​ Probability of Improvement (PI) 采集函数会选择具有最大可能性提高当前最大的 $f(x+)$ 值的点（在能增加最大值的候选点中选择概率最大的点）作为下一个查询点，即：

$$\boldsymbol{x}_{t+1}= \arg \max_x (PI(x))=\arg \max_x P \left( f(\boldsymbol{x})≥f(\boldsymbol{x}^+) + \epsilon\right)$$

其中：

• $\epsilon$ 为一个较小的正数
• $ \boldsymbol{x}^+ = \arg\max _{\boldsymbol{x} \in D}f(\boldsymbol{x})$，表示当前已观测到的最大值的位置

如果采用高斯过程回归作为代理模型，上式则转变为：

$$\boldsymbol{x}_{t+1}= \arg \max_x (PI(x))=\arg \max_x \Phi \left( \frac{\mu_t(\boldsymbol{x}) - f(\boldsymbol{x}^+) - \epsilon}{\sigma_t(\boldsymbol{x})} \right)$$

其中：

• $\Phi(⋅)$ 表示标准正态分布累积分布函数
• $\mu_t, \sigma_t$ 分别代表在 $t$ 时刻的高斯过程的均值和方差函数

Expected Improvement (EI)

​ PI 仅关注了有多大的可能性能够提高，而没有关注能够提高多少。Expected Improvement (EI) 则会选择具有最大期望提高的点作为下一个查询点，即：

$$\boldsymbol{x}_{t+1}=\arg \max_x \mathbb{E}\left(\max\{0, ||h_{t+1}(\boldsymbol{x})−f(\boldsymbol{x}^+) || \}\right)$$

其中：

• $h_{t+1}$ 为代理模型在 $t+1$ 步的后验均值
• $x^+$ 为在前 $t$ 时刻中 $f$ 取得最大值的位置（目前为止遇见的最大函数值）

如果采用高斯过程作为代理模型，上式则转变为：

$$EI (x) =\left\{ \begin{array}{l} \left(\mu_t(\boldsymbol{x})-f(\boldsymbol{x}^+)- \epsilon \right)\Phi (Z) + \sigma_t(x) \phi(Z) \quad \text{if }\sigma_t(x) \gt 0 \\ 0 \quad \text{if }\sigma_t(x) \gt 0\\ \end{array} \right. \\ Z = \frac{\mu_t(\boldsymbol{x}) - f(\boldsymbol{x}^+) - \epsilon}{\sigma_t(x)}$$

其中 $\Phi(⋅)$ 表示标准正态分布累积分布函数，$\phi(⋅)$ 表示标准正态分布概率密度函数。类似 PI，EI 也可以利用 $\epsilon$ 来权衡探索和开发，增加 $\epsilon$ 的值会更加倾向进行探索

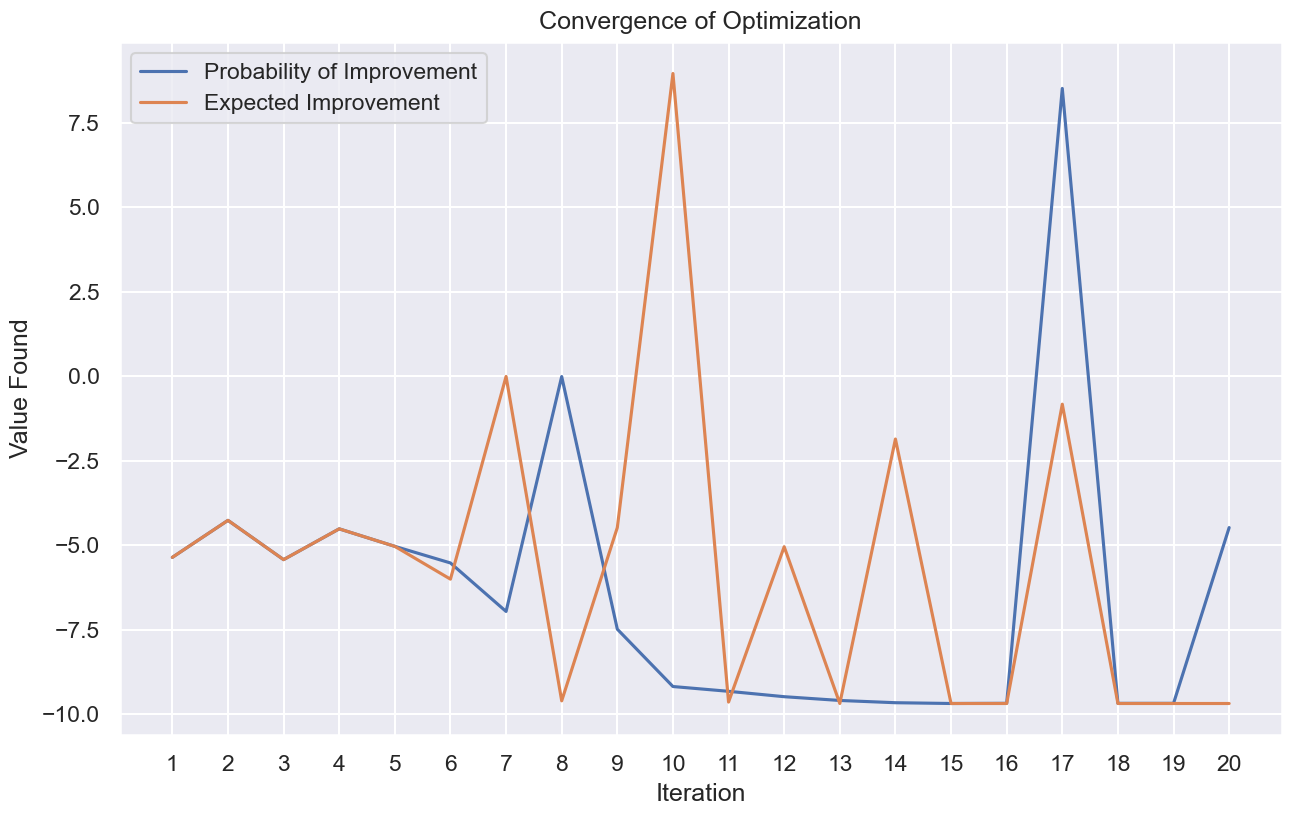
实际实验证明一般情况下 EI 函数的表现比 PI 更好：