3D Gaussian Splatting

图形学前置知识

点云数据：

​ 三维坐标系统中的一组向量集合，每一个点包含三维坐标，可能包含颜色信息（RGB）或反射强度信息（Intensity，表示每个点云中点的反射、反射率、反射强度）。 本质上是3D空间中无序、无结构的海量数据点的集合。它的获取方式多种多样，在 3D Gaussian Splatting 中主要会通过二维影像进行三维重建，在重建过程中获取点云数据

3D 表面形状表示：

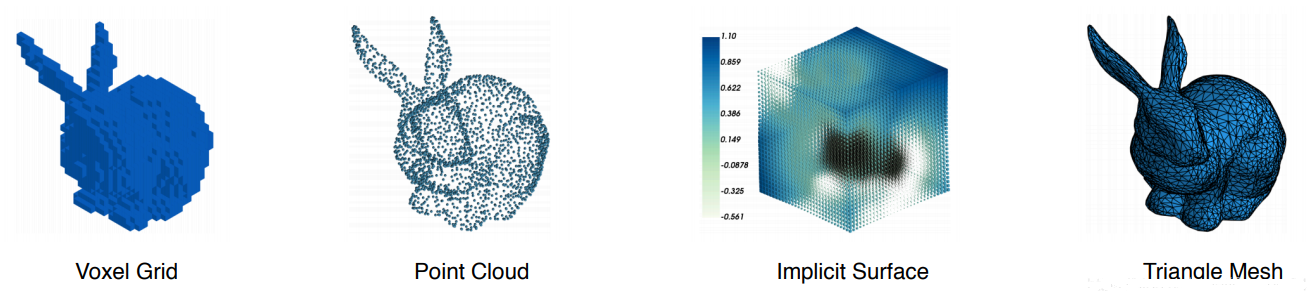
• 多边形网格表示（Polygon Mesh Representation）：由连接顶点的边和面组成的结构。它是表示复杂几何形状的一种常见方法。多边形网格通常由三角形或四边形构成，但也可以包含更高阶的多边形。多边形网格可以表示平面几何形状，也可以通过三角剖分等技术表示曲面或复杂形状（不光滑）
• 参数曲面表示（Parametric Surface Representation）：通过参数化方程来表示的曲面。它使用参数化坐标（通常是二维参数）来描述曲面上的点。参数曲面可以通过数学函数或参数化曲线来生成，例如贝塞尔曲线和贝塞尔曲面。参数曲面表示适用于光滑的曲面和复杂的形状（光滑）
• 体素表示（Voxel Representation）：三维空间中的一个像素或体素元素，类似于二维图像中的像素。体素表示将三维空间划分为规则的体素网格（小立方体），并使用每个体素的属性（如密度、颜色）来表示物体的形状和属性。体素表示适用于体积数据和体绘制应用，例如医学图像和体渲染

渲染（重建任务的逆任务）：

​ 将三维场景转换为二维图像的过程。它是计算机图形学领域的一个重要任务，基于已知的3D模型、材质属性、光照条件等信息，使用确定性的算法计算出2D图像。这个过程中，输入（3D场景）是明确的，输出（2D图像）是通过模拟物理光学现象计算得出的，渲染技术主要有提渲染和光栅化：

光栅化（Rasterization）：

​ 光栅化是一种将3D几何对象（通常是多边形网格和参数曲面）转换为2D图像的过程。它首先确定哪些像素被几何形状覆盖，然后计算这些像素的颜色值。找到所有被几何原型所占据的所有像素点然后逐个渲染这些点，得到图像的显示效果。光栅化渲染速度快，用于实时渲染，但渲染效果可能不如体渲染

体渲染 (Volume Rendering)：

​ 体渲染用于直接从体积数据（如CT或MRI扫描得到的数据集）生成图像，而不需要先将数据转化为表面模型。它可以显示物体内部的细节。能够展示物体内部结构，非常适合医学成像、气象学等领域

• 光栅化技术是 Gaussian Splatting 算法采用的技术，Nerf 采用的是体渲染技术

3D Gaussian Splatting 是2023 年提出的技术，他是属于图形学和 CV 的内容，简而言之，Gaussian Splatting提出了一种三维重建（3D Gaussian）和配套的渲染方式（Splatting），能够

• 迅速地重建现实世界中的场景
• 用重建的场景渲染新视角图片，可以做到实时渲染且效果很好

3D Gaussian Splatting

3D Gaussian Splatting 渲染的过程可以用下图表示：

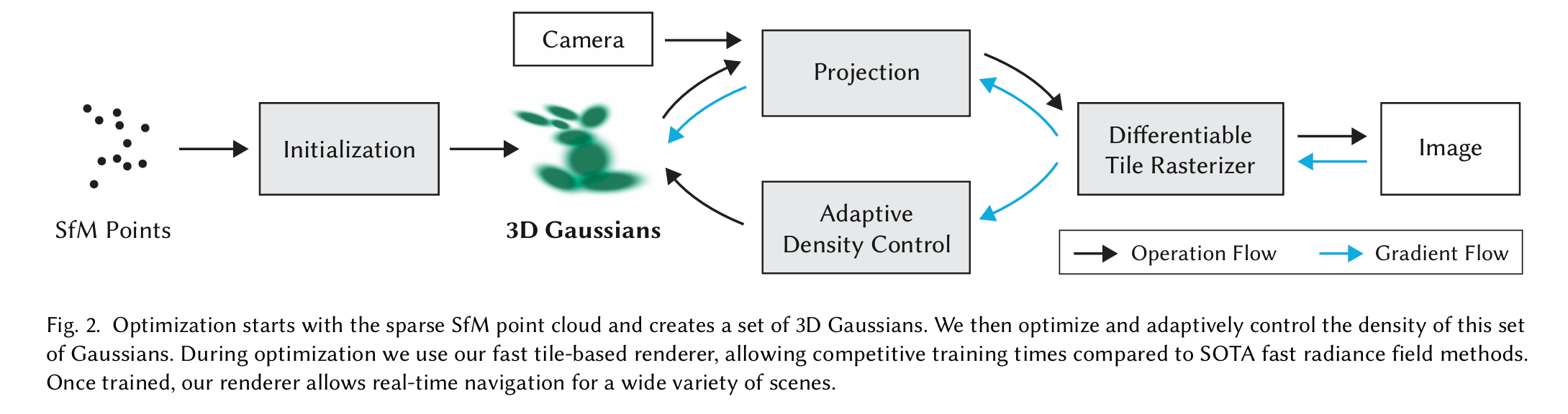
1. 先用一组图片（多视角图片）来获得一组点云（SFM 算法，不是重点不讲解）
2. 再使用这一组点云初始化一组 3D Gaussians 椭球
3. 将 3D Gaussians 椭球投影到相机坐标（世界坐标投影到相机坐标）
4. 使用光栅化渲染技术渲染出图像
5. 对比渲染的图像和原图的区别，将 loss 返回到 3D Gaussians 来进行优化（类似反向传播）

我们重点介绍投影，渲染和优化部分的算法

Gaussians and initialization

​ 在这里指出高斯椭球和多元正态分布天生的内在联系，多元正态分布的概率密度表达式如下：

$$p\left( \boldsymbol{x}\right) = \frac{1}{( 2\pi )^{\frac{n}{2}}\left| \boldsymbol{\Sigma}\right|^{\frac{1}{2}}}\exp \left\{ -\frac{1}{2}{( \boldsymbol{x - \mu})^T\boldsymbol{\Sigma}^{-1}(\boldsymbol{x - \mu}) }\right\} \\ \Rightarrow ( \boldsymbol{x-\mu})^T\boldsymbol{\Sigma}^{-1}(\boldsymbol{x-\mu})=\chi^2(\alpha)$$

令 $p(\boldsymbol{x}) = \text{const}$，$\boldsymbol{x} \in \mathbb{R}^3$ ，则可以推出 $(x,y,z)$ 在空间内描述的就是一个椭球

​ 为了初始化高斯椭球，为了保证渲染效果，直觉上我们需要初始化椭球的几个参数是：

• 位置（对应多元正态分布的均值）
• 旋转信息与长度信息（对应多元正态分布的协方差矩阵）
• 颜色（选择球谐函数为基函数，用球谐函数参数和基函数的系数来描述，$3 \times 4^2=48$）
• 不透明度信息（opacity）

Projection

​ 这个投影是将世界坐标系投影到 2D 平面坐标，这个过程可以被看作是两步投影：从世界坐标系到相机坐标系的变换 + 从相机坐标系到2D图像平面的投影

世界坐标系到相机坐标系的变换

​ 这一步骤也称为“外参变换”，它涉及到将三维空间中的点从世界坐标系转换到相机坐标系。这个变换可以通过一个包含旋转和平移信息的 $4\times4$ 变换矩阵 $T_{cw}$ 来完成，该矩阵描述了相机相对于世界坐标系的位置和方向：

$$\boldsymbol{p}_c=\boldsymbol{W} \boldsymbol{p}_w$$

其中：

• $p_w$ 是世界坐标系中的点（注意是坐标四维的，除了三维坐标还加上了一个齐次项维度 1）
• $p_c$ 是转换后的相机坐标系中的点
• $T_{cw}$ 包括了一个旋转矩阵 $R$（一个正交阵） 和一个平移向量 $t$，可以写为：

$$\boldsymbol{W} = \left[ \begin{matrix} \boldsymbol{R}_{3\times3} & \boldsymbol{t} \\ \boldsymbol{0}& 1 \\ \end{matrix} \right]$$

推导过程：

$$\left[ \begin{array}{c} x_2\\ y_2\\ z_2\\ \end{array} \right] =R_{3\times 3}\left[ \begin{array}{c} x_2\\ y_2\\ z_2\\ \end{array} \right] +\left[ \begin{array}{c} t_1\\ t_2\\ t_3\\ \end{array} \right] \\ \text{Let} \quad \boldsymbol{p}=[x, y, z, 1]^T \\ \boldsymbol{p}_2= \left[\begin{matrix} \boldsymbol{R} & \boldsymbol{t} \\ \boldsymbol{0} & 1 \end{matrix}\right] \boldsymbol{p}_1$$

从相机坐标系到2D图像平面的投影

​ 这一步骤其实分为两步，第一步是相机坐标系到图像坐标的投影（投影是线性变化），第二部是图像坐标向像素坐标的变换（这一步是非线性变换），在这里我们不学习成像的原理，把它们合成一步变换来描述，这个变换将相机坐标系中的 3D 点投影到像素 2D 图像平面上。这个过程使用相机的内部参数，如焦距、主点位置等，这些参数通常被组织成一个 $3\times3$ 的相机内参矩阵 $J$，这个投影过程可以表示为：

$$\boldsymbol{P}_{img} = \boldsymbol{J}\cdot \left[\begin{matrix}\boldsymbol{P}_c \\ 1\end{matrix}\right]$$

• 一个很自然的问题是：为什么 $J$ 矩阵的形状是 $3 \times 3$，原因在于在这个变换中，有一个步骤是 3D 到 2D 的转化时对第三个坐标归一化了，因此转化坐标的之后有一个元素是个常数项没有含义，因此变换后坐标还是二维，并不存在问题

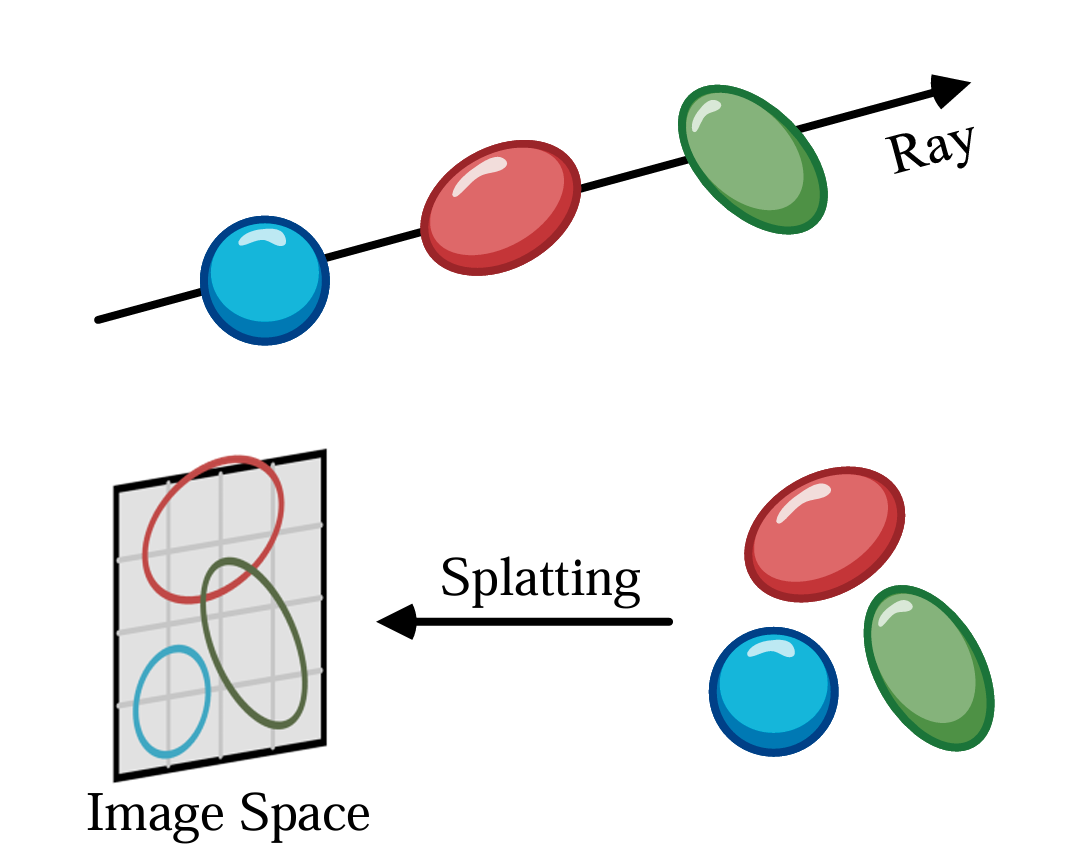
坐标变换对 Gaussian 椭球的影响：

​ 使用上面的变换，将高斯椭球投影到 2D 图像平面上，描述这个高斯椭球方程为：

$${\left( \boldsymbol{x} - \boldsymbol{\mu}\right) }^T{\boldsymbol{\Sigma}}^{-1}\left( {\boldsymbol{x} - \boldsymbol{\mu}}\right)=\chi^2(\alpha)$$

代入

$$\boldsymbol{x}'=\boldsymbol{R}_{3 \times 3}\boldsymbol{x} + \boldsymbol{t}$$

形状的协方差矩阵 $\boldsymbol{\Sigma}$ 的变化表示为：

$$\boldsymbol{\Sigma}'=\boldsymbol{JW\Sigma W}^T\boldsymbol{J}^T$$

3D Gaussian Splatting 快速渲染：

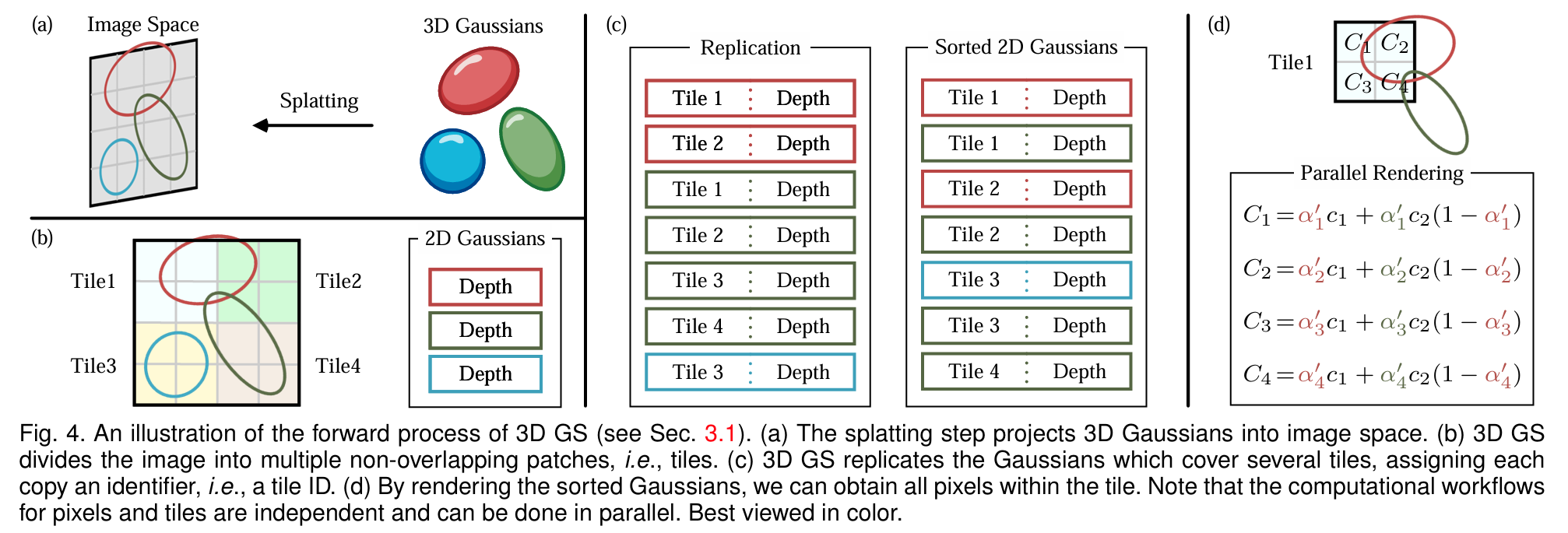
1. 将三维椭球 splate 到二维的视图平面（只保留视锥以内的椭球）
2. 将视图平面划分为一定数量的栅格，同时开一片存储区将椭球到视图平面的深度值记录下来
3. 给存储区的椭球开一个副本，不仅记录每个椭球对应的深度值，还要记录每个椭球 splate 到了哪些栅格里面（上图中的©图，一种颜色代表对应一个椭球）
4. 将这个副本区的椭球记录按照栅格的序号和高斯椭球的深度排序（重要性：栅格序号 > 高斯椭球深度）
   1. 使用像素渲染，将每个像素上的颜色用栅格内的，覆盖该像素位置的高斯椭球的不透明度和颜色来渲染

​ 看到这里可能会好奇，栅格的划分有什么作用，最终我们渲染的操作还是要对像素级别进行的，那为什么不直接划分像素进行渲染而是先划分栅格再划分像素呢？答案是节省计算成本，直接对像素进行排序是非常耗时且耗存储区的，我们使用了栅格先做一个大概的划分，提前做一个快速深度排序，减少时间成本。伪代码示意如下：

自适应点云分布方式：

• Pruning（减少 Gaussians）：
  • 减少伪影出现，将不透明度大于一定阈值的高斯椭球（黑色的高斯椭球）给剔除掉，能够去除渲染图像中的黑影
  • 处理欠采样问题，将不透明度小于一定阈值的高斯椭球（太透明了可以忽略）给剔除掉，能够减少高斯椭球的数量
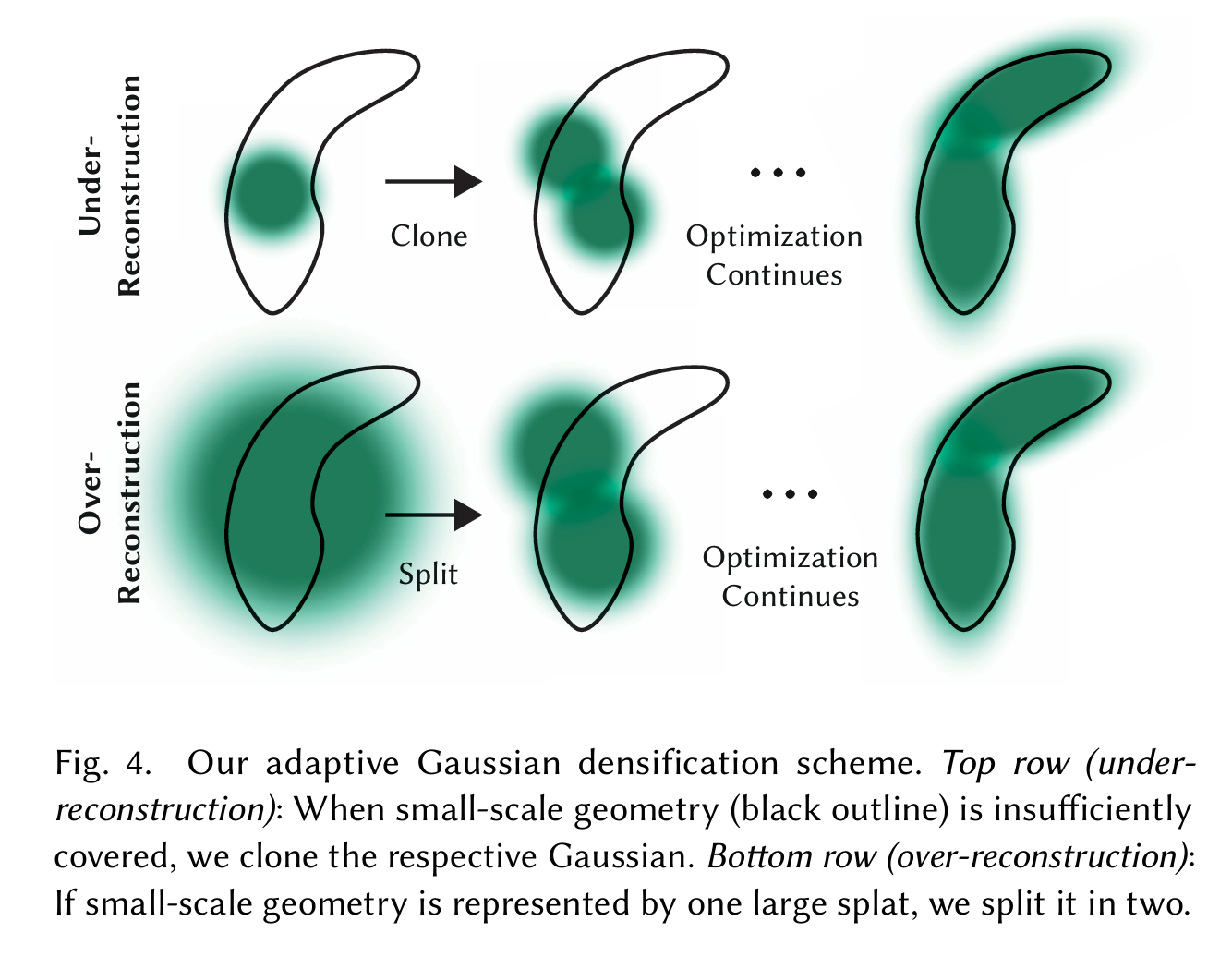
• Desification（增加 Gaussians）：为了达到渲染质量高的目的，不能仅仅改变高斯椭球的参数，有时还需要增加高斯椭球的数量，这时候分为两个情况（使用空间位置梯度判定），under-reconstruction 和 over-reconstruction：
  • under-reconstruction：对于重建不足的区域将 Gaussian 给复制一份
  • over-reconstruction：对于过重建的区域将 Gaussian 给分裂开

算法的伪代码描述如下：