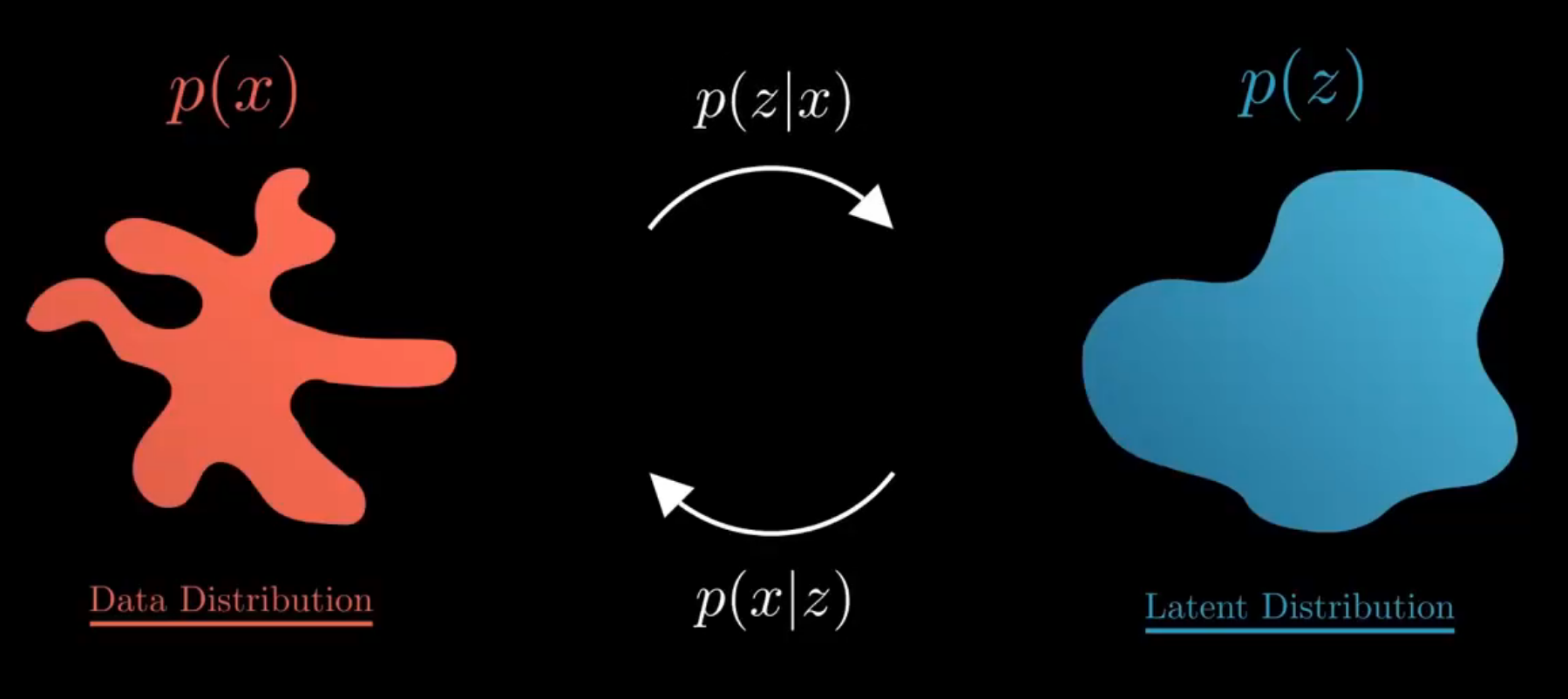
给定从某个分布中抽取的观察样本x x x p ( x ) p(x) p ( x )
一旦模型学会了如何近似真实的数据分布,我们就可以使用这个模型生成新的样本。这意味着我们可以根据学到的分布规律创造出新的数据点,这些新数据点应该与训练集中的数据具有相似的特征或属性。这对于诸如图像生成、文本创作等任务非常有用
总的来说,生成式模型可以分为以下几类:
likelihood based model(基于似然性的生成模型):
目标是学习一个能为观察到的数据样本分配高似然值的模型
主要包括:自回归模型(Autoregressive Models),正态流(Normalizing Flows)变分自编码器(Variational Autoencoders, VAEs)
energy based model(基于能量的模型):
学习一个灵活的能量函数,该函数随后被标准化以形成分布
这种方法与基于似然性的模型有相似之处,但侧重点在于能量函数的学习
score based model(基于得分的生成模型):
与基于能量的模型高度相关,但不是直接学习能量函数本身,而是学习能量模型的得分(即梯度)作为神经网络
得分模型通常用于指导样本生成过程,通过调整样本使其更符合目标分布
特殊的 diffusion model 和 GAN,后面我们会从似然和分数的角度看 diffusion model
E p ( x ) log p ( x ) q ( x ) = ∫ p ( x ) log p ( x ) q ( x ) d x = D K L ( p ( x ) ∣ ∣ q ( x ) ) p ( x ∣ y ) = p ( y ∣ x ) p ( x ) p ( y ) \mathbb{E}_{p(x)}\log\frac{p(x)}{q(x)}=\int p(x) \log \frac{p(x)}{q(x)}dx = D_{KL}(p(x)||q(x)) \\
p(x|y)=\frac{p(y|x)p(x)}{p(y)}
E p ( x ) log q ( x ) p ( x ) = ∫ p ( x ) log q ( x ) p ( x ) d x = D K L ( p ( x ) ∣ ∣ q ( x ) ) p ( x ∣ y ) = p ( y ) p ( y ∣ x ) p ( x )
对于许多模态,我们可以将我们观察到的数据视为由一个相关的未见潜在变量(latent variable)表示或生成的,这个潜在变量可以用随机变量z \boldsymbol{z} z z z z
为什么生成低维的潜在表示而不是高维的表示呢?柏拉图的洞穴寓言中,居民只能看到三维物体的二维投影,但可以通过这些投影推理出三维物体的性质。类似地,我们可以通过观察到的数据来近似潜在的高层次表示。但是对于生成式模型,学习高维潜在表示通常是徒劳的,除非有很强的先验知识。这是因为高维潜在空间中的大部分信息可能是冗余的或无关的 ,同时低维潜在表示可以看作是一种数据压缩技术,有助于减少冗余信息。
低维潜在表示能够揭示出描述观察数据的语义上有意义的结构,帮助生成新的数据样本并理解数据的本质特征
在生成模型中,我们通常考虑观察数据x \boldsymbol{x} x z \boldsymbol{z} z p ( x , z ) p(\boldsymbol{x,z}) p ( x , z ) x \boldsymbol{x} x z \boldsymbol{z} z x \boldsymbol{x} x p ( x ) p(\boldsymbol{x}) p ( x )
为了从联合分布p ( x , z ) p(\boldsymbol{x,z}) p ( x , z ) x \boldsymbol{x} x p ( x ) p(\boldsymbol{x}) p ( x )
p ( x ) = ∫ p ( x , z ) d z p(\boldsymbol{x})=\int p(\boldsymbol{x,z})d\boldsymbol{z} p ( x ) = ∫ p ( x , z ) d z
p ( x ) = p ( x , z ) p ( z ∣ x ) p(\boldsymbol{x})=\frac{p(\boldsymbol{x,z})}{p(\boldsymbol{z| x})} p ( x ) = p ( z ∣ x ) p ( x , z )
我们的目标是最大化x \boldsymbol{x} x max log p ( x ) \max\log p(\boldsymbol{x}) max log p ( x )
使用 p ( x ) = ∫ p ( x , z ) d z p(\boldsymbol{x})=\int p(\boldsymbol{x,z})d\boldsymbol{z} p ( x ) = ∫ p ( x , z ) d z
使用 p ( x ) = p ( x , z ) p ( z ∣ x ) p(\boldsymbol{x})=\frac{p(\boldsymbol{x,z})}{p(\boldsymbol{z| x})} p ( x ) = p ( z ∣ x ) p ( x , z ) p ( z ∣ x ) p(\boldsymbol{z|x}) p ( z ∣ x )
因此我们目标转变为最大化证据下界,下面我们去证明优化这个式子是合理的:
E L B O = E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) ] ELBO=\mathbb{E}_{q_\phi(\boldsymbol{z|x})}\left[\log \frac{p(\boldsymbol{x,z})}{q_\boldsymbol{\phi}(z|x)} \right]
E L B O = E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p ( x , z ) ]
\begin{align}
\log p(\boldsymbol{x}) &=\log \int p(\boldsymbol{x,z})d\boldsymbol{z} \\
&=\log \int \frac{p(\boldsymbol{x,z})q_\phi (\boldsymbol{z|x})}{q_\phi (\boldsymbol{z|x})}d\boldsymbol{z} \\
&=\log \mathbb{E}_{q_\phi(z|x)} \left[ \frac{p(\boldsymbol{x,z})}{q_\phi (\boldsymbol{z|x})} \right] \\
&\ge \mathbb{E}_{q_\phi(z|x)}\left[ \log \frac{p(\boldsymbol{x,z})}{q_\phi (\boldsymbol{z|x})}\right]
\end {align}
\begin{align}
\log p(\boldsymbol{x}) &=\int q_\phi(\boldsymbol{z|x})\log p(\boldsymbol{x})dz \\
&=\mathbb{E}_{q_\phi(z|x)} \left[ \log p(\boldsymbol{x})\right] \\
&=\mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(\boldsymbol{x,z})}{p(\boldsymbol{z|x})}\right] \\
&=\mathbb{E}_{q_\phi(z|x))} \left[ \log \frac{p(\boldsymbol{x,z}) q_{\phi}(\boldsymbol{z|x})}{p(\boldsymbol{z|x}) q_{\phi}(\boldsymbol{z|x})}\right] \\
&=\mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(\boldsymbol{x,z}) }{ q_{\phi}(\boldsymbol{z|x})}\right] + \mathbb{E}_{q_\phi(\boldsymbol{z|x})} \left[ \frac{q_{\phi} (\boldsymbol{z|x})}{p(\boldsymbol{z|x})} \right]\\
&=\mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(\boldsymbol{x,z}) }{ q_{\phi}(\boldsymbol{z|x})}\right] + D_{KL}(q_\phi (\boldsymbol{z|x})\ \| \ p(\boldsymbol{z|x}))\\
&\ge \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(\boldsymbol{x,z}) }{ q_\phi(\boldsymbol{z|x})}\right]
\end{align}
q ϕ ( z ∣ x ) q_\phi(\boldsymbol{z|x}) q ϕ ( z ∣ x ) p ( z ∣ x ) p(\boldsymbol{z|x}) p ( z ∣ x ) 数据的对数似然概率是固定的,我们优化 ELBO 的时候,KL 散度也会变小趋向于 0,这样我们可以同时让 ELBO 趋于 log p ( x ) \log p(\boldsymbol{x}) log p ( x )
E p ϕ ( z ∣ x ) log p ( x , z ) p ϕ ( z ∣ x ) = E p ϕ ( z ∣ x ) log p ( z ∣ x ) p ( x ) p ϕ ( z ∣ x ) ∼ E p ϕ ( z ∣ x ) log p ( x ) = log p ( x ) \mathbb{E}_{p_\phi(z|x)}\log \frac{p(\boldsymbol{x,z})}{p_\phi(\boldsymbol{z|x})} = \mathbb{E}_{p_\phi(z|x)}\log \frac{p(\boldsymbol{z|x})p(\boldsymbol{x})}{p_\phi(\boldsymbol{z|x})}\\
\sim \mathbb{E}_{p_\phi(z|x)}\log p(\boldsymbol{x}) = \log p(\boldsymbol{x})
E p ϕ ( z ∣ x ) log p ϕ ( z ∣ x ) p ( x , z ) = E p ϕ ( z ∣ x ) log p ϕ ( z ∣ x ) p ( z ∣ x ) p ( x ) ∼ E p ϕ ( z ∣ x ) log p ( x ) = log p ( x )
在 VAE 中,我们的训练目标是在最大化数据的对数似然的同时,保持潜在空间的平滑性和连续性。因此同样使用了 ELBO 为目标函数进行优化,使用了变分推理的技巧:
E q ϕ ( z ∣ x ) [ log p ( x , z ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p θ ( x ∣ z ) p ( z ) q ϕ ( z ∣ x ) ] = E q ϕ ( z ∣ x ) [ log p θ ( x ∣ z ) ] ⏟ reconstruction term − D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ) ) ⏟ prior matching term \mathbb{E}_{q_\phi(\boldsymbol{z\mid x})}\left[\log \frac{p(\boldsymbol{x,z})}{q_\phi(z|x)} \right]=E_{q_\phi(\boldsymbol{z|x})}\left[\log \frac{p_\theta(\boldsymbol{x|z})p(\boldsymbol{z})}{q_\phi(\boldsymbol{z|x})} \right] \\
=\underbrace{\mathbb{E}_{q_\phi(\boldsymbol{z\mid x})}\left[\log p_\theta(\boldsymbol{x|z}) \right]}_\text{reconstruction term} - \underbrace{D_{KL}(q_\phi (\boldsymbol{z|x}) || p(\boldsymbol{z}))}_\text{prior matching term}
E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p ( x , z ) ] = E q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p θ ( x ∣ z ) p ( z ) ] = reconstruction term E q ϕ ( z ∣ x ) [ log p θ ( x ∣ z ) ] − prior matching term D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ) )
E q ϕ ( z ∣ x ) [ log p θ ( x ∣ z ) ] \mathbb{E}_{q_\phi(\boldsymbol{z| x})}\left[\log p_\theta(\boldsymbol{x|z}) \right] E q ϕ ( z ∣ x ) [ log p θ ( x ∣ z ) ] z \boldsymbol{z} z 考虑为什么不使用 z z z ,即不使用 E [ log p θ ( x ∣ z ) ] \mathbb{E}[\log p_\theta (\boldsymbol{x|z})] E [ log p θ ( x ∣ z ) ] D K L ( q ϕ ( x ∣ z ) ∥ p ( z ) ) D_{KL}(q_\phi (\boldsymbol{x|z}) \ \| \ p(\boldsymbol{z})) D K L ( q ϕ ( x ∣ z ) ∥ p ( z ) ) p ( z ) p(\boldsymbol{z}) p ( z )
因此 VAE 的优化目标转化为最大化 reconstruction item 和最小化 prior matching item,我们假设隐变量为高斯分布(VAE 本身就是要将隐变量的分布给正规化的),设:
Posterior Distribution: q ϕ ( z ∣ x ) = N ( z ; μ ϕ ( x ) , σ ϕ 2 ( x ) I ) Prior Distribution: p ( z ) = N ( z ; 0 , I ) \text{Posterior Distribution:}\quad q_\phi (\boldsymbol{z|x}) = \mathcal{N}(\boldsymbol{z;\mu_\phi (x),\sigma_\phi^2(x)I}) \\
\text{Prior Distribution:}\quad p(\boldsymbol{z}) = \mathcal{N}(\boldsymbol{z;0,I})
Posterior Distribution: q ϕ ( z ∣ x ) = N ( z ; μ ϕ ( x ) , σ ϕ 2 ( x ) I ) Prior Distribution: p ( z ) = N ( z ; 0 , I )
如果使用蒙特卡洛方法,优化目标可以表示为:
arg max ϕ , θ E q ϕ ( z ∣ x ) [ log p θ ( x ∣ z ) ] − D K L ( q ϕ ( x ∣ z ) ∥ p ( z ) ) ≈ arg max ϕ , θ ∑ l = 1 L log p θ ( x ∣ z ( l ) ) − D K L ( q ϕ ( x ∣ z ) ∥ p ( z ) ) {\arg \max}_{\phi, \theta} \mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z| x})}\left[\log p_\theta(\boldsymbol{x|z}) \right] - D_{KL}(q_\phi (\boldsymbol{x|z}) \ \| \ p(\boldsymbol{z})) \\
\approx {\arg \max}_{\phi, \theta} \sum_{l=1}^L \log p_\theta(\boldsymbol{x|z}^{(l)}) - D_{KL}(q_\phi (\boldsymbol{x|z}) \ \| \ p(\boldsymbol{z}))
arg max ϕ , θ E q ϕ ( z ∣ x ) [ log p θ ( x ∣ z ) ] − D K L ( q ϕ ( x ∣ z ) ∥ p ( z ) ) ≈ arg max ϕ , θ l = 1 ∑ L log p θ ( x ∣ z ( l ) ) − D K L ( q ϕ ( x ∣ z ) ∥ p ( z ) )
{ z ( l ) } l = 1 L \{\boldsymbol{z}^{(l)}\}_{l=1}^L { z ( l ) } l = 1 L q ϕ ( x ∣ z ) q_\phi(\boldsymbol{x|z}) q ϕ ( x ∣ z )
使用重参数化技巧,把随机采样的变量表示为噪声变量的确定函数 (epsilon 的梯度不需要计算,应为他根本不是模型的参数):
x ∼ N ( x ; μ , σ 2 ) ⇒ x = μ + σ ϵ ϵ ∼ N ( ϵ ; 0 , I ) For VAE: z = μ ϕ ( x ) + σ ϕ ( x ) ⊙ ϵ x \sim \mathcal{N}(x;\mu, \sigma^2) \Rightarrow x=\mu + \sigma_\epsilon \quad \epsilon \sim \mathcal{N}(\epsilon;\boldsymbol{0,I})\\
\text{For VAE:} \quad \boldsymbol{z}=\boldsymbol{\mu_\phi(x)}+\boldsymbol{\sigma_\phi(x)} \odot \boldsymbol{\epsilon}
x ∼ N ( x ; μ , σ 2 ) ⇒ x = μ + σ ϵ ϵ ∼ N ( ϵ ; 0 , I ) For VAE: z = μ ϕ ( x ) + σ ϕ ( x ) ⊙ ϵ
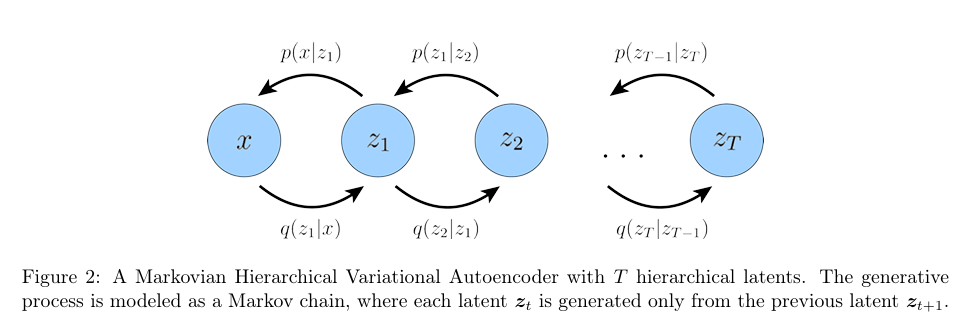
层次变分自编码器(Hierarchical Variational Autoencoder, HVAE)是一种 VAE 的扩展,它可以处理多层潜在变量。在这种框架下,潜在变量本身被解释为由更高层次、更为抽象的潜在变量生成。
在一般的 HVAE 中,每个潜在变量可以依赖于所有先前的潜在变量,在本文中,我们只专注于一个特殊情况:马尔可夫层次变分自编码器(Markovian Hierarchical Variational Autoencoder, MHVAE)。在 MHVAE 中,生成过程是一个马尔可夫链;也就是说,沿着层次结构的每一步转换都是马尔可夫性的,其中每个潜在变量 z t \boldsymbol{z}_t z t z t + 1 \boldsymbol{z}_{t+1} z t + 1
p ( x , z 1 : T ) = p ( z T ) p θ ( x ∣ z 1 ) ∏ t = 2 T p θ ( z t − 1 ∣ z t ) q ϕ ( z 1 : T ∣ x ) = q ϕ ( z 1 ∣ x ) ∏ t = 2 T q ϕ ( z t ∣ z t − 1 ) p(\boldsymbol{x,z}_{1:T})=p(\boldsymbol{z}_T)p_\theta(\boldsymbol{x|z_1}) \prod_{t=2}^{T}p_\theta(\boldsymbol{z_{t-1}|z_t})\\
q_\phi(\boldsymbol{z_{1:T}|x})=q_\phi(\boldsymbol{z_1|x}) \prod_{t=2}^{T}q_\phi(\boldsymbol{z_t|z_{t-1}})
p ( x , z 1 : T ) = p ( z T ) p θ ( x ∣ z 1 ) t = 2 ∏ T p θ ( z t − 1 ∣ z t ) q ϕ ( z 1 : T ∣ x ) = q ϕ ( z 1 ∣ x ) t = 2 ∏ T q ϕ ( z t ∣ z t − 1 )
ELBO 可以拓展概念为:
\begin{align}
\log p(\boldsymbol{x})= &\log \int p(\boldsymbol{x,z_{1:T}})d\boldsymbol {z_{1:T}}=\log \int\frac{p(\boldsymbol{x,z_{1:T}})q_\phi(\boldsymbol{z_{1:T}|x})}{q_\phi(\boldsymbol{z_{1:T}|x})}d \boldsymbol{z_{1:T}}\\
&=\log\mathbb{E}_{q_\phi(\boldsymbol{z_{1:T}|x})}\left[\frac{p(\boldsymbol{x,z_{1:T}})}{q_\phi(\boldsymbol{z_{1:T}|x})}\right]\\
&\geq\mathbb{E}_{q_\phi(\boldsymbol{z_{1:T}|x})}\left[\log\frac{p(\boldsymbol{x,z_{1:T}})}{q_\phi(\boldsymbol{z_{1:T}|x})}\right]
\end{align}
再使用 MHVAE 的性质:
E q ϕ ( z 1 : T ∣ x ) [ log p ( x , z 1 : T ) q ϕ ( z 1 : T ∣ x ) ] = E q ϕ ( z 1 : T ∣ x ) [ log p ( z T ) p θ ( x ∣ z 1 ) ∏ t = 2 T p θ ( z t − 1 ∣ z t ) q ϕ ( z 1 ∣ x ) ∏ t = 2 T q ϕ ( z t ∣ z t − 1 ) ] \mathbb{E}_{q_\phi(z_{1:T}|x)}\left[\log\frac{p(\boldsymbol{x,z_{1:T}})}{q_\phi(\boldsymbol{z_{1:T}|x})}\right]=\mathbb{E}_{q_\phi(z_{1:T}|x)}\left[\log\frac{p(z_{T})p_{\theta}(\boldsymbol{x|z_1})\prod_{t=2}^{T}p_{\theta}(z_{t-1}|z_{t})}{q_\phi(\boldsymbol{z_1|x})\prod_{t=2}^{T}q_{\phi}(z_{t}|z_{t-1})}\right]
E q ϕ ( z 1 : T ∣ x ) [ log q ϕ ( z 1 : T ∣ x ) p ( x , z 1 : T ) ] = E q ϕ ( z 1 : T ∣ x ) [ log q ϕ ( z 1 ∣ x ) ∏ t = 2 T q ϕ ( z t ∣ z t − 1 ) p ( z T ) p θ ( x ∣ z 1 ) ∏ t = 2 T p θ ( z t − 1 ∣ z t ) ]
对于 VDM 模型,它的潜变量之间的关系和 MHVAE 十分相似,马尔科夫性保证了:
q ( x t ∣ x 0 : t − 1 ) = q ( x t ∣ x t − 1 ) ⇒ q ( x 1 : T ∣ x 0 ) = q ( x 1 ∣ x 0 ) ⋅ q ( x 2 ∣ x 0 , x 1 ) … q ( x T ∣ x 0 , x 1 , … , x T − 1 ) = q ( x 1 ∣ x 0 ) ⋅ q ( x 2 ∣ x 1 ) … q ( x T ∣ x T − 1 ) q(\boldsymbol{x_t|x_{0:t-1}})=q(\boldsymbol{x_t|x_{t-1}}) \\
\Rightarrow q(\boldsymbol{x_{1:T}|x_0}) = q(\boldsymbol{x_1|x_0}) \cdot q(\boldsymbol{x_2|x_0,x_1}) \dots q(\boldsymbol{x_T|x_0,x_1, \dots, x_{T-1}}) \\
=q(\boldsymbol{x_1|x_0}) \cdot q(\boldsymbol{x_2|x_1}) \dots q(\boldsymbol{x_T|x_{T-1}})
q ( x t ∣ x 0 : t − 1 ) = q ( x t ∣ x t − 1 ) ⇒ q ( x 1 : T ∣ x 0 ) = q ( x 1 ∣ x 0 ) ⋅ q ( x 2 ∣ x 0 , x 1 ) … q ( x T ∣ x 0 , x 1 , … , x T − 1 ) = q ( x 1 ∣ x 0 ) ⋅ q ( x 2 ∣ x 1 ) … q ( x T ∣ x T − 1 )
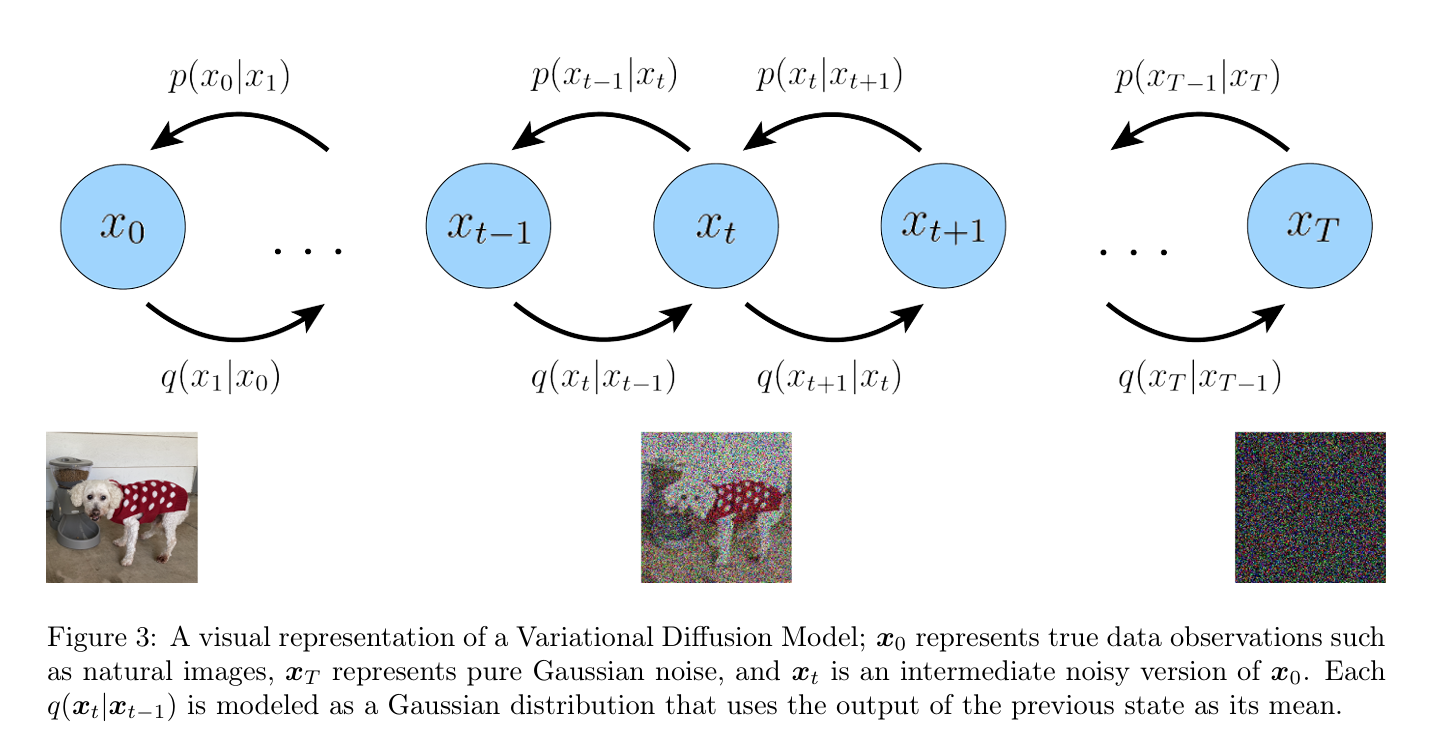
其他的只是过程从 encode-decode 变成了 noise-denoise,我们记真实样本照片为 x 0 \boldsymbol{x}_0 x 0 x 1 , … , x T \boldsymbol{x}_1, \dots, \boldsymbol{x}_T x 1 , … , x T
q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) p ( x 0 : T ) = p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) p ( x T ) = N ( x T ; 0 , I ) q(\boldsymbol{x}_{1:T}|\boldsymbol{x}_{0})=\prod_{t=1}^{T}q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1}) \\
q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1})=\mathcal{N}(\boldsymbol{x}_{t};\sqrt{\alpha_{t}}\boldsymbol{x}_{t-1},(1-\alpha_{t})\mathbf{I}) \\
p(\boldsymbol{x}_{0:T})=p(\boldsymbol{x}_{T})\prod_{t=1}^{T}p_{\boldsymbol{\theta}}(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t}) \\
p(\boldsymbol{x}_{T})=\mathcal{N}(\boldsymbol{x}_{T};\mathbf{0},\mathbf{I})
q ( x 1 : T ∣ x 0 ) = t = 1 ∏ T q ( x t ∣ x t − 1 ) q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) p ( x 0 : T ) = p ( x T ) t = 1 ∏ T p θ ( x t − 1 ∣ x t ) p ( x T ) = N ( x T ; 0 , I )
约束条件分析:
q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1})=\mathcal{N}(\boldsymbol{x}_{t};\sqrt{\alpha_{t}}\boldsymbol{x}_{t-1},(1-\alpha_{t})\mathbf{I}) q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I )
和 HVAE 不同的是,VDM 是不需要学加噪过程的,即 encoder 的参数是不需要学习的,我们只需要关心去噪的过程,因此下面我们的 p p p q q q
在下面的公式中,由于每一步的加噪过程是需要学习的,因此将涉及到 t t t t + 1 t +1 t + 1 θ \theta θ
和 HVAE 相似,VDM 可以通过最大化 ELBO 来优化模型:
log p ( x ) = log ∫ p ( x 0 : T ) d x 1 : T = log ∫ p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) q ( x 1 : T ∣ x 0 ) d x 1 : T = log E q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ≥ E q ( x 1 : T ∣ x 0 ) [ log p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) ∏ t = 1 T q ( x t ∣ x t − 1 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 2 T p θ ( x t − 1 ∣ x t ) q ( x T ∣ x T − 1 ) ∏ t = 1 T − 1 q ( x t ∣ x t − 1 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 1 T − 1 p θ ( x t ∣ x t + 1 ) q ( x T ∣ x T − 1 ) ∏ t = 1 T − 1 q ( x t ∣ x t − 1 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) p θ ( x 0 ∣ x 1 ) q ( x T ∣ x T − 1 ) ] + E q ( x 1 : T ∣ x 0 ) [ log ∏ t = 1 T − 1 p θ ( x t ∣ x t + 1 ) q ( x t ∣ x t − 1 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] + E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) q ( x T ∣ x T − 1 ) ] + E q ( x 1 : T ∣ x 0 ) [ ∑ t = 1 T − 1 log p θ ( x t ∣ x t + 1 ) q ( x t ∣ x t − 1 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] + E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) q ( x T ∣ x T − 1 ) ] + ∑ t = 1 T − 1 E q ( x 1 : T ∣ x 0 ) [ log p θ ( x t ∣ x t + 1 ) q ( x t ∣ x t − 1 ) ] = E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] + E q ( x T − 1 , x T ∣ x 0 ) [ log p ( x T ) q ( x T ∣ x T − 1 ) ] + ∑ t = 1 T − 1 E q ( x t − 1 , x t , x t + 1 ∣ x 0 ) [ log p θ ( x t ∣ x t + 1 ) q ( x t ∣ x t − 1 ) ] = E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] ⏟ reconstruction term − E q ( x T − 1 ∣ x 0 ) [ D K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) ] ⏟ prior matching term − ∑ t = 1 T − 1 E q ( x t − 1 , x t + 1 ∣ x 0 ) [ D KL ( q ( x t ∣ x t − 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ] ⏟ consistency term \begin{aligned}
\log p(\boldsymbol{x})& =\log \int p(\boldsymbol{x}_{0:T})d\boldsymbol{x}_{1:T} \\
&=\log\int\frac{p(\boldsymbol{x}_{0:T})q(\boldsymbol{x}_{1:T}|\boldsymbol{x}_0)}{q(\boldsymbol{x}_{1:T}|\boldsymbol{x}_{0})}d\boldsymbol{x}_{1:T} \\
&=\log\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0)}}
\frac{p(\boldsymbol{x}_{0:T})}{q(\boldsymbol{x_{1:T}|x_0})} \\
&\geq\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0)}}\left[\log\frac{p(\boldsymbol{x}_{0:T})}{q(\boldsymbol{x_{1:T}|x_0)}}\right] \\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}\left[\log\frac{p(\boldsymbol{x}_T)\prod_{t=1}^Tp_\theta(\boldsymbol{x_{t-1}|x_t})}{\prod_{t=1}^Tq(\boldsymbol{x_t|x_{t-1}})}\right] \\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}\left[\log\frac{p(\boldsymbol{x}_T)p_\theta(\boldsymbol{x_0|x_1})\prod_{t=2}^Tp_\theta(\boldsymbol{x_{t-1}|x_t)}}{q(\boldsymbol{x_T|x_{T-1}})\prod_{t=1}^{T-1}q(\boldsymbol{x_t|x_{t-1}})}\right] \\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0)}}\left[\log\frac{p(\boldsymbol{x}_T)p_\theta(\boldsymbol{x_0|x_1})\prod_{t=1}^{T-1}p_\theta(\boldsymbol{x_t|x_{t+1}})}{q(\boldsymbol{x_T|x_{T-1}})\prod_{t=1}^{T-1}q(\boldsymbol{x_t|x_{t-1}})}\right] \\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}\left[\log\frac{p(\boldsymbol{x}_T)p_\theta(\boldsymbol{x_0|x_1)}}{q(\boldsymbol{x_T|x_{T-1}})}\right]+\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}\left[\log \prod_{t=1}^{T-1}\frac{p_\theta(\boldsymbol{x_t|x_{t+1}})}{q(\boldsymbol{x_t|x_{t-1}})}\right] \\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}\left[\log p_\theta(\boldsymbol{x_0|x_1})\right]+\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0)}}\left[\log\frac{p(\boldsymbol{x}_T)}{q(\boldsymbol{x_T|x_{T-1})}}\right]+\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0)}}\left[\sum_{t=1}^{T-1}\log\frac{p_\theta(\boldsymbol{x_t|x_{t+1})}}{q(\boldsymbol{x_t|x_{t-1}})}\right] \\
&=\mathbb{E}_{q(\boldsymbol{x}_{1:T}|\boldsymbol{x}_0)}\left[\log p_\theta(\boldsymbol{x}_0|\boldsymbol{x}_1)\right]+\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0)}}\left[\log\frac{p(\boldsymbol{x}_T)}{q(\boldsymbol{x_T|x_{T-1}})}\right]+\sum_{t=1}^{T-1}\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0)}}\left[\log\frac{p_\theta(\boldsymbol{x_t|x_{t+1})}}{q(\boldsymbol{x_t|x_{t-1})}}\right] \\
&=\mathbb{E}_{q(\boldsymbol{x_1|x_0})}\left[\log p_\theta(\boldsymbol{x_0|x_1})\right]+\mathbb{E}_{q(\boldsymbol{x_{T-1},x_T|x_0})}\left[\log\frac{p(\boldsymbol{x}_T)}{q(\boldsymbol{x_T|x_{T-1}})}\right]+\sum_{t=1}^{T-1}\mathbb{E}_{q(\boldsymbol{x_{t-1},x_t,x_{t+1}|x_0)}}\left[\log\frac{p_\theta(\boldsymbol{x_t|x_{t+1}})}{q(\boldsymbol{x_t|x_{t-1}})}\right] \\
&=\underbrace{\mathbb{E}_{q(\boldsymbol{x_1|x_0)}}\left[\log p_\theta(\boldsymbol{x_0|x_1})\right]}_{\text{reconstruction term}}-\underbrace{\mathbb{E}_{q(\boldsymbol{x_{T-1}|x_0)}}\left[D_{KL}(q(\boldsymbol{x_T|x_{T-1}})\parallel p(\boldsymbol{x}_T))\right]}_{\text{prior matching term}} \\
&-\sum_{t=1}^{T-1}\underbrace{\mathbb{E}_{q(\boldsymbol{x}_{t-1},\boldsymbol{x_{t+1}|x_0)}}\left[D_{\text{KL}}(q(\boldsymbol{x_t|x_{t-1}})\parallel p_\theta(\boldsymbol{x_t|x_{t+1}}))\right]}_{\text{consistency term}}
\end{aligned}
log p ( x ) = log ∫ p ( x 0 : T ) d x 1 : T = log ∫ q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) d x 1 : T = log E q ( x 1 : T ∣ x 0 ) q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ≥ E q ( x 1 : T ∣ x 0 ) [ log q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ] = E q ( x 1 : T ∣ x 0 ) [ log ∏ t = 1 T q ( x t ∣ x t − 1 ) p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) ] = E q ( x 1 : T ∣ x 0 ) [ log q ( x T ∣ x T − 1 ) ∏ t = 1 T − 1 q ( x t ∣ x t − 1 ) p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 2 T p θ ( x t − 1 ∣ x t ) ] = E q ( x 1 : T ∣ x 0 ) [ log q ( x T ∣ x T − 1 ) ∏ t = 1 T − 1 q ( x t ∣ x t − 1 ) p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 1 T − 1 p θ ( x t ∣ x t + 1 ) ] = E q ( x 1 : T ∣ x 0 ) [ log q ( x T ∣ x T − 1 ) p ( x T ) p θ ( x 0 ∣ x 1 ) ] + E q ( x 1 : T ∣ x 0 ) [ log t = 1 ∏ T − 1 q ( x t ∣ x t − 1 ) p θ ( x t ∣ x t + 1 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] + E q ( x 1 : T ∣ x 0 ) [ log q ( x T ∣ x T − 1 ) p ( x T ) ] + E q ( x 1 : T ∣ x 0 ) [ t = 1 ∑ T − 1 log q ( x t ∣ x t − 1 ) p θ ( x t ∣ x t + 1 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] + E q ( x 1 : T ∣ x 0 ) [ log q ( x T ∣ x T − 1 ) p ( x T ) ] + t = 1 ∑ T − 1 E q ( x 1 : T ∣ x 0 ) [ log q ( x t ∣ x t − 1 ) p θ ( x t ∣ x t + 1 ) ] = E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] + E q ( x T − 1 , x T ∣ x 0 ) [ log q ( x T ∣ x T − 1 ) p ( x T ) ] + t = 1 ∑ T − 1 E q ( x t − 1 , x t , x t + 1 ∣ x 0 ) [ log q ( x t ∣ x t − 1 ) p θ ( x t ∣ x t + 1 ) ] = reconstruction term E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] − prior matching term E q ( x T − 1 ∣ x 0 ) [ D K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) ] − t = 1 ∑ T − 1 consistency term E q ( x t − 1 , x t + 1 ∣ x 0 ) [ D KL ( q ( x t ∣ x t − 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ]
E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] \mathbb{E}_{q(\boldsymbol{x_1|x_0)}}\left[\log p_\theta(\boldsymbol{x_0|x_1})\right] E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] D K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) D_{KL}(q(\boldsymbol{x_T|x_{T-1}})\parallel p(\boldsymbol{x}_T)) D K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) x T − 1 \boldsymbol{x}_{T-1} x T − 1 x T \boldsymbol{x}_T x T 在 T T T E q ( x t − 1 , x t + 1 ∣ x 0 ) [ D KL ( q ( x t ∣ x t − 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ] \mathbb{E}_{q(\boldsymbol{x}_{t-1},\boldsymbol{x_{t+1}|x_0)}}\left[D_{\text{KL}}(q(\boldsymbol{x_t|x_{t-1}})\parallel p_\theta(\boldsymbol{x_t|x_{t+1}}))\right] E q ( x t − 1 , x t + 1 ∣ x 0 ) [ D KL ( q ( x t ∣ x t − 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ] 对每一步 x T x_T x T ,(这一步是最耗时的,每一步 x T \boldsymbol{x}_T x T
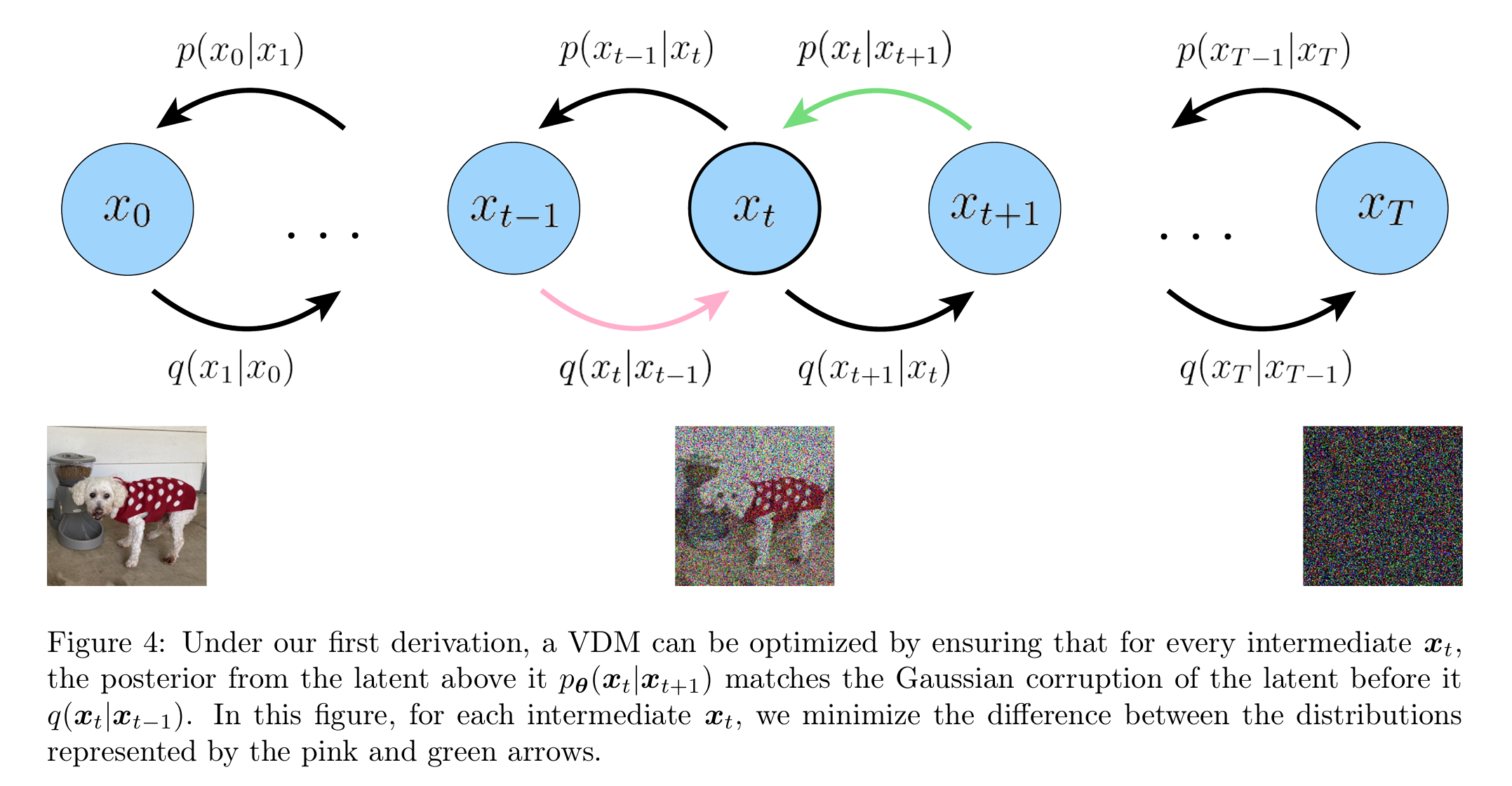
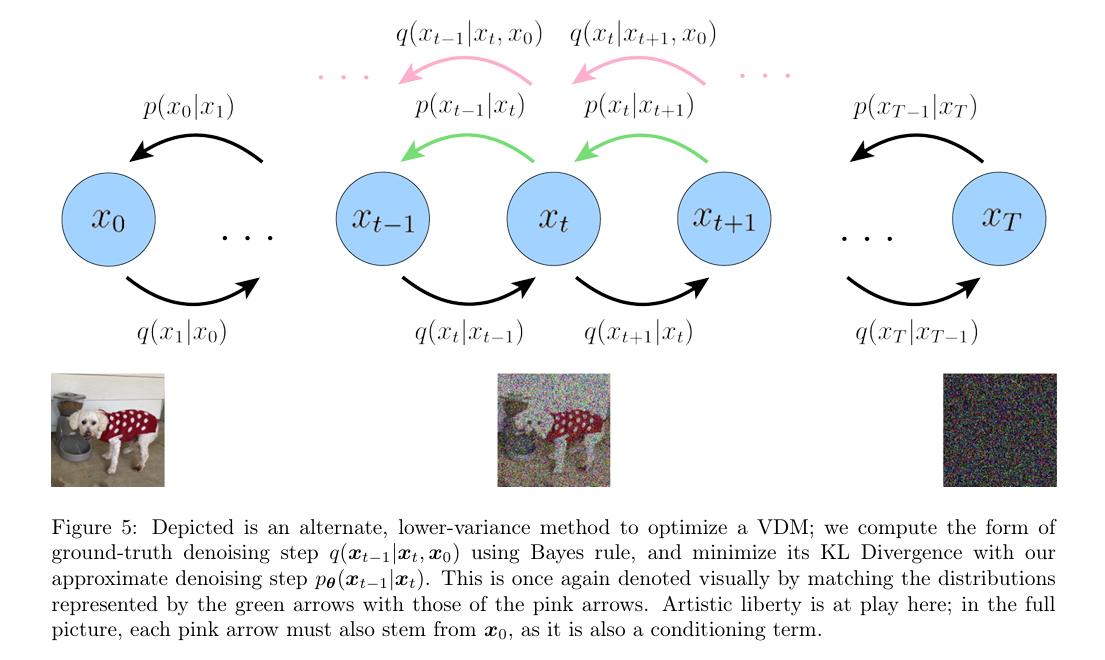
在上面的推导下,ELBO 的所有项都被计算为期望值,因此可以使用蒙特卡洛估计来近似。然而,实际上使用刚刚推导的这些项来优化 ELBO 效果是不好的;因为一致性项(consistency term)是在每个时间步长上对两个随机变量 x T − 1 \boldsymbol{x}_{T-1} x T − 1 x T + 1 \boldsymbol{x}_{T+1} x T + 1 T T T T T T
log p ( x ) ≥ E q ( x 1 : T ∣ x 0 ) [ log p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) ∏ t = 1 T q ( x t ∣ x t − 1 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 2 T p θ ( x t − 1 ∣ x t ) q ( x 1 ∣ x 0 ) ∏ t = 2 T q ( x t ∣ x t − 1 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) p θ ( x 0 ∣ x 1 ) q ( x 1 ∣ x 0 ) + log ∏ t = 2 T p θ ( x t − 1 ∣ x t ) q ( x t ∣ x t − 1 ) ] \begin{aligned}\log p(\boldsymbol{x})
&\geq\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}\left[\log\frac{p(\boldsymbol{x}_{0:T})}{q(\boldsymbol{x_{1:T}|x_0})}\right]\\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}\left[\log\frac{p(\boldsymbol{x}_T)\prod_{t=1}^Tp_\theta(\boldsymbol{x_{t-1}|x_t)}}{\prod_{t=1}^Tq(\boldsymbol{x_t|x_{t-1}})}\right]\\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0)}}\left[\log\frac{p(\boldsymbol{x}_T)p_\theta(\boldsymbol{x_0|x_1})\prod_{t=2}^Tp_\theta(\boldsymbol{x_{t-1}|x_t})}{q(\boldsymbol{x_1|x_0)}\prod_{t=2}^Tq(\boldsymbol{x_t|x_{t-1}})}\right]\\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x}_0)}\left[\log\frac{p(\boldsymbol{x_T})p_\theta(\boldsymbol{x_0|x_1})}{q(\boldsymbol{x_1|x}_0)}+\log\prod_{t=2}^T\frac{p_\theta(\boldsymbol{x_{t-1}|x}_t)}{q(\boldsymbol{x_t|x_{t-1}})}\right]\\
\end{aligned}
log p ( x ) ≥ E q ( x 1 : T ∣ x 0 ) [ log q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ] = E q ( x 1 : T ∣ x 0 ) [ log ∏ t = 1 T q ( x t ∣ x t − 1 ) p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) ] = E q ( x 1 : T ∣ x 0 ) [ log q ( x 1 ∣ x 0 ) ∏ t = 2 T q ( x t ∣ x t − 1 ) p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 2 T p θ ( x t − 1 ∣ x t ) ] = E q ( x 1 : T ∣ x 0 ) [ log q ( x 1 ∣ x 0 ) p ( x T ) p θ ( x 0 ∣ x 1 ) + log t = 2 ∏ T q ( x t ∣ x t − 1 ) p θ ( x t − 1 ∣ x t ) ]
因此为了继续化简下一步我们的目标是将这三个概率关联:
p θ ( x t − 1 ∣ x t ) q ( x t ∣ x t − 1 ) q ( x 1 : T ∣ x 0 ) p_\theta(\boldsymbol{x_{t-1}|x_t}) \quad q(\boldsymbol{x_t|x_{t-1}}) \quad q(\boldsymbol{x_{1:T}|x_0})
p θ ( x t − 1 ∣ x t ) q ( x t ∣ x t − 1 ) q ( x 1 : T ∣ x 0 )
由于马尔科夫性,我们可以注意到:
q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) q(\boldsymbol{x_t|x_{t-1}})=q(\boldsymbol{x_t|x_{t-1},x_0})=\frac{q(\boldsymbol {x_{t-1}|x_t,x_0})q(\boldsymbol{x_t|x_0})}{q(\boldsymbol{x_{t-1}|x_0})}
q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x 0 ) q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 )
log p ( x ) ≥ E q ( x 1 : T ∣ x 0 ) [ log p ( ( x T ) p θ ( x 0 ∣ x 1 ) q ( x 1 ∣ x 0 ) + log ∏ t = 2 T p θ ( x t − 1 ∣ x t ) q ( x t ∣ x t − 1 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) p θ ( x 0 ∣ x 1 ) q ( x 1 ∣ x 0 ) + log ∏ t = 2 T p θ ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) ] approximation = E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) p θ ( x 0 ∣ x 1 ) q ( x 1 ∣ x 0 ) + log q ( x 1 ∣ x 0 ) q ( x T ∣ x 0 ) + log ∏ t = 2 T p θ ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x 0 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) p θ ( x 0 ∣ x 1 ) q ( x 1 ∣ x 0 ) + ∑ i = 2 m log p θ ( x i − 1 ∣ x i ) q ( x i − 1 ∣ x i , x 0 ) ] = E q ( x 1 : T ∣ x 0 ) [ log p ( x 0 ∣ x 1 ) ] + E q ( x 1 : T ∣ x 0 ) [ log p ( x T ) q ( x 1 ∣ x 0 ) ] + ∑ t = 2 T E q ( x 1 : T ∣ x 0 ) [ log p θ ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t , x 0 ) ] = E q ( x 1 ∣ x 0 ) [ log p ( x 0 ∣ x 1 ) ] + E q ( x t ∣ , x 0 ) [ log p ( x ) q ( x 1 ∣ x 0 ) ] + ∑ t = 2 T E q ( x T ∣ x 0 ) [ log p θ ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t , x 0 ) ] = E q ( x 1 ∣ x 0 ) [ log p ( x 0 ∣ x 1 ) ] ⏟ reconstruction item + D K L ( q ( x T ∣ x 0 ) ∣ ∣ p ( x T ) ) ⏟ prior matching item + ∑ t = 2 T E q ( x T ∣ x 0 ) [ D K L ( p θ ( x t − 1 ∣ x t ) ∣ ∣ q ( x t − 1 ∣ x t , x 0 ) ) ] ⏟ denoising item \begin{aligned}
\log p(\boldsymbol{x})
&\geq\mathbb{E}_{q(\boldsymbol{x_{1:T}|x}_0)}\left[\log\frac{p((\boldsymbol{x_T})p_\theta(\boldsymbol{x_0|x_1})}{q(\boldsymbol{x_1|x}_0)}+\log\prod_{t=2}^T\frac{p_\theta(\boldsymbol{x_{t-1}|x}_t)}{q(\boldsymbol{x_t|x_{t-1}})}\right]\\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x}_0)}\left[\log\frac{p(\boldsymbol{x_T})p_\theta(\boldsymbol{x_0|x_1})}{q(\boldsymbol{x_1|x_0})}+\log\prod_{t=2}^T\frac{p_\theta(\boldsymbol{x_{t-1}|x_t})}{\frac{q(\boldsymbol {x_{t-1}|x_t,x_0})\cancel{q(\boldsymbol{x_t|x_0})}}{\cancel{q(\boldsymbol{x_{t-1}|x_0})}}}\right] \quad \text{approximation}\\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}\left[\log\frac{p(\boldsymbol{x}_T)p_\theta(\boldsymbol{x_0|x_1})}{\cancel{q(\boldsymbol{x_1|x_0})}}+\log\frac{\cancel{q(\boldsymbol{x_1|x_0})}}{q(\boldsymbol{x_T|x_0})} +\log\prod_{t=2}^T\frac{p_\theta(\boldsymbol{x_{t-1}|x}_t)}{q(\boldsymbol{x_{t-1}|x}_0)}\right]\\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}\left[\log\frac{p(\boldsymbol{x}_T)p_\theta(\boldsymbol{x_0|x_1})}{q(\boldsymbol{x_1|x_0})}+\sum_{i=2}^{m}\log\frac{p_\theta(\boldsymbol{x_{i-1}|x_i})}{q(\boldsymbol{x_{i-1}|x_i, x_0})}\right]\\
&=\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}
\left[\log p(\boldsymbol{x_0|x_1})\right]+\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}\left[\log\frac{p(\boldsymbol{x}_T)}{q(\boldsymbol{x_1|x_0})}\right]+\sum_{t=2}^{T}\mathbb{E}_{q(\boldsymbol{x_{1:T}|x_0})}\left[\log\frac{p_\theta(\boldsymbol{x_{t-1}|x_t})}{q(\boldsymbol{x_{t-1}|x_t,x_0})}\right] \\
&=\mathbb{E}_{q(\boldsymbol{x_1|x_0})}\left[\log p(\boldsymbol{x_0|x_1})\right] +
\mathbb{E}_{q(\boldsymbol{x_t|,x_0})}\left[\log\frac{p(\boldsymbol{x})}{q(\boldsymbol{x_1|x_0})}\right]+
\sum_{t=2}^T\mathbb{E}_{q(\boldsymbol{x_T|x_0})}\left[\log\frac{p_\theta(\boldsymbol{x_{t-1}|x_t})}{q(\boldsymbol{x_{t-1}|x_t,x_0})}\right]\\
&=\underbrace{\mathbb{E}_{q(\boldsymbol{x_1|x_0})}\left[\log p(\boldsymbol{x_0|x_1})\right]}_\text{reconstruction item} +
\underbrace{D_{KL}(q(\boldsymbol{x_T|x_0})||p(\boldsymbol{x}_T))}_\text{prior matching item} +
\sum_{t=2}^T\underbrace{\mathbb{E}_{q(\boldsymbol{x_T|x_0})}\left[D_{KL}\left( p_\theta(\boldsymbol{x_{t-1}|x_t}) || q(\boldsymbol{x_{t-1}|x_t,x_0}) \right)\right]}_\text{denoising item}
\end{aligned}
log p ( x ) ≥ E q ( x 1 : T ∣ x 0 ) [ log q ( x 1 ∣ x 0 ) p ( ( x T ) p θ ( x 0 ∣ x 1 ) + log t = 2 ∏ T q ( x t ∣ x t − 1 ) p θ ( x t − 1 ∣ x t ) ] = E q ( x 1 : T ∣ x 0 ) ⎣ ⎢ ⎡ log q ( x 1 ∣ x 0 ) p ( x T ) p θ ( x 0 ∣ x 1 ) + log t = 2 ∏ T q ( x t − 1 ∣ x 0 ) q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) p θ ( x t − 1 ∣ x t ) ⎦ ⎥ ⎤ approximation = E q ( x 1 : T ∣ x 0 ) [ log q ( x 1 ∣ x 0 ) p ( x T ) p θ ( x 0 ∣ x 1 ) + log q ( x T ∣ x 0 ) q ( x 1 ∣ x 0 ) + log t = 2 ∏ T q ( x t − 1 ∣ x 0 ) p θ ( x t − 1 ∣ x t ) ] = E q ( x 1 : T ∣ x 0 ) [ log q ( x 1 ∣ x 0 ) p ( x T ) p θ ( x 0 ∣ x 1 ) + i = 2 ∑ m log q ( x i − 1 ∣ x i , x 0 ) p θ ( x i − 1 ∣ x i ) ] = E q ( x 1 : T ∣ x 0 ) [ log p ( x 0 ∣ x 1 ) ] + E q ( x 1 : T ∣ x 0 ) [ log q ( x 1 ∣ x 0 ) p ( x T ) ] + t = 2 ∑ T E q ( x 1 : T ∣ x 0 ) [ log q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) ] = E q ( x 1 ∣ x 0 ) [ log p ( x 0 ∣ x 1 ) ] + E q ( x t ∣ , x 0 ) [ log q ( x 1 ∣ x 0 ) p ( x ) ] + t = 2 ∑ T E q ( x T ∣ x 0 ) [ log q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) ] = reconstruction item E q ( x 1 ∣ x 0 ) [ log p ( x 0 ∣ x 1 ) ] + prior matching item D K L ( q ( x T ∣ x 0 ) ∣ ∣ p ( x T ) ) + t = 2 ∑ T denoising item E q ( x T ∣ x 0 ) [ D K L ( p θ ( x t − 1 ∣ x t ) ∣ ∣ q ( x t − 1 ∣ x t , x 0 ) ) ]
D K L ( q ( x T ∣ x 0 ) ∣ ∣ p ( x T ) ) D_{KL}(q(\boldsymbol{x_T|x_0})||p(\boldsymbol{x}_T)) D K L ( q ( x T ∣ x 0 ) ∣ ∣ p ( x T ) ) E q ( x T ∣ x 0 ) [ D K L ( p ( x t − 1 ∣ x t ) ∣ ∣ q ( x t − 1 ∣ x t , x 0 ) ) ] \mathbb{E}_{q(\boldsymbol{x_T|x_0})}\left[D_{KL}\left( p(\boldsymbol{x_{t-1}|x_t}) || q(\boldsymbol{x_{t-1}|x_t,x_0}) \right)\right] E q ( x T ∣ x 0 ) [ D K L ( p ( x t − 1 ∣ x t ) ∣ ∣ q ( x t − 1 ∣ x t , x 0 ) ) ]
Understanding Diffusion Models: A Unified Perspective