Guided Filtering

Guided Filtering是一种图像处理技术，它主要用于边缘保留平滑，即在去除噪声或细节的同时保持图像中的重要边缘，引导滤波（Guided Filtering）和双边滤波（BF）、最小二乘滤波（WLS）是三大边缘保持（Edge-perserving）滤波器。当然，引导滤波的功能不仅仅是边缘保持，只有当引导图是原图的时候，它就成了一个边缘保持滤波器

Guided Filtering

问题建模：

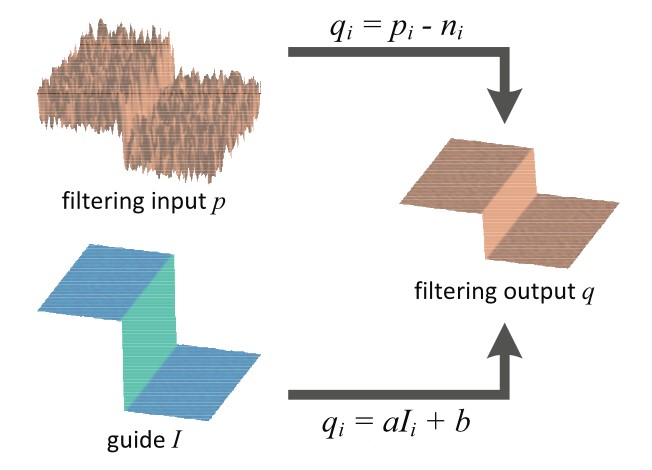
对于一个输入的图像p，通过引导图像I，经过滤波后得到输出图像q，其中p和1都是算法的输入。引导滤波定义了如下所示的一个线性滤波过程，对于i位置的像素点，得到的滤波输出是一个加权平均值：

q_{i} = \sum_j W_{ij} (I) \ {p_j}

其中，i和j分别表示像素下标。 $W_{ij}$ 是只和引导图像I相关的滤波核。该滤波器相对于 $p$ 是线性的。导向滤波的一个重要假设是输出图像 $q$ 和引导图像I在滤波窗口 $w_k$ 上存在局部线性关系：

q_i = a_k I_i + b_k,\ \forall {i} \in w_k

对于一个以 $r$ 为半径的确定的窗口 $w_k$ ， $(a_k ,b_k)$ 也将是唯一确定的常量系数。这就保证了在一个局部区域里，如果引导图像 $I$ 有一个边缘的时候，输出图像 $q$ 也保持边缘不变，因为对于相邻的像素点而言，存在 $\nabla {q} = {a}\nabla {I}$ 。因此只要求解得到了系数 $a$ ， $b$ 也就得到了输出 $q$ 。同时认为输入图像中非边缘区域又不平滑的地方视为噪声 $n$ ，就有 $q_i = p_i - n_i$ 。最终的目标就是最小化这个噪声。对于每一个滤波窗口，该算法在最小二乘意义上的最优化可表示为：

\min {\sum_{i \in w_k} ( q_i - p_i)^2} \\ \Rightarrow \min {\sum_{i \in w_k} ( a_k I_i + b_k - p_i)^2}

最后，引入一个正则化参数 $\epsilon$ 避免 $a_k$ 过大，得到滤波窗口内的损失函数：

J\left( a_k,b_k\right) = \sum_{i \in w_k}\left(\left( a_k I_i + b_k - p_i\right)^2 + \epsilon a_k^2\right)

求解最优化过程（对参数求偏导）：

\frac{\partial J}{a_k} = \sum_{i \in w_k}\left( 2(a_k I_i + b_k - p_i)I_i + 2\epsilon a_k \right) = 0 \\ \frac{\partial J}{b_k} = \sum_{i \in w_k} 2(a_k I_i + b_k - p_i) = 0

最优化问题的解

为了简便表示，记：

\overline{p_k}=\frac{1} {card(w_k) }\sum_{i \in w_k}p_i, \ \ \overline{I_k}=\frac{1}{card(w_k) } I_i, \ \sigma_k^2 = \overline{I_k^2} - \overline{I_k}^2

解得最优化问题的解为：

a_k = \frac{\overline{p_k I_k}-\overline{p_k}\overline{I_k}}{\sigma_k^2 + \epsilon } \\ b_k = \overline{p}_k - a_k\overline{I}_k

边缘保持

对于该算法，当 $I = p$ 时，即输入图像和引导图像是同一副图像时，该算法即成为一个边缘保持滤波器。同时，方程的解也可作如下表示：

a_k = \frac{\sigma_k^2}{\sigma_k^2 + \epsilon } \\ b_k = \left( {1 - a_k}\right) {\overline{p}}_k

从中可以看出， $\epsilon$ 在这里相当于界定平滑区域和边缘区域的阈值

考虑以下两种情况：

Case 1: 平坦区域。如果在某个滤波窗口内，该区域是相对平滑的，方差 $\sigma_k^2$ 将远远小于 $\epsilon$ 。从而 $a_1\approx 0,b_k \approx \bar{p}_k$ 。相当于对该区域作均值滤波
Case 2: 高方差区域。相反，如果该区域是边缘区域，方差很大， $\sigma_k^2$ 将远远大于 $\epsilon$ 。从而 $a_k \approx 1,b_k \approx 0$ 。相当于在区域保持原有梯度

代码实现：

import PIL
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
def box_filter(x, r):
    """
    Box filter implementation.
    """
    ch = x.shape[1]
    kernel_size = 2 * r + 1
    # 创建一个填充矩阵
    pad = torch.nn.ReplicationPad2d(r)
    padded_x = pad(x)
    
    # 使用卷积操作求每个像素点的邻域的平均值
    kernel = torch.ones((ch, 1, kernel_size, kernel_size), device=x.device)
    output = F.conv2d(padded_x, kernel, padding=0, groups=ch)
    return output

class GuidedFilter(torch.nn.Module):
    def __init__(self, radius, eps=1e-8):
        super(GuidedFilter, self).__init__()
        self.radius = radius
        self.eps = eps

    def forward(self, x, y):
        n_x = box_filter(x, self.radius)
        mean_x = n_x / (2 * self.radius + 1) ** 2
        mean_y = box_filter(y, self.radius) / (2 * self.radius + 1) ** 2
        
        # D(x) = E(x^2) - E^2(x)
        corr_x = box_filter(x * x, self.radius)
        var_x = corr_x / (2 * self.radius + 1) ** 2 - mean_x * mean_x
        
        cov_xy = box_filter(x * y, self.radius) / (2 * self.radius + 1) ** 2 - mean_x * mean_y
        
        a = cov_xy / (var_x + self.eps)
        b = mean_y - a * mean_x
        
        mean_a = box_filter(a, self.radius) / (2 * self.radius + 1) ** 2
        mean_b = box_filter(b, self.radius) / (2 * self.radius + 1) ** 2
        
        return mean_a * x + mean_b

# 示例使用
if __name__ == '__main__':
    input_image = PIL.Image.open('./cat.jpg').convert('RGB')
    np_image = np.array(input_image)
    input_image = torch.from_numpy(np_image).permute(2, 0, 1).unsqueeze(0).float() / 255.0
    # 假设输入图像为单通道灰度图像
    guide_image = input_image
    # 创建 Guided Filter 对象
    guided_filter = GuidedFilter(radius=5, eps=1e-4)
    # 应用滤波
    filtered_image = guided_filter(guide_image, input_image)
    filtered_image = F.max_pool2d(filtered_image, kernel_size=2, stride=2, padding=1)
    filtered_image = filtered_image.squeeze(0).permute(1, 2, 0).numpy()
    fig, axes = plt.subplots(1, 2)
    axes[0].imshow(np_image)
    axes[0].set_title('Original Image')
    axes[1].imshow(filtered_image)
    axes[1].set_title('Filtered Image')
    plt.show()

    print("Filtered image shape:", filtered_image.shape)

代码简洁之处就在于使用 box_filter 函数来简化计算，对照着上文 $a_k,b_k$ 的计算公式即可理解

example

差分卷积——边缘检测上一篇

Segformer 下一篇