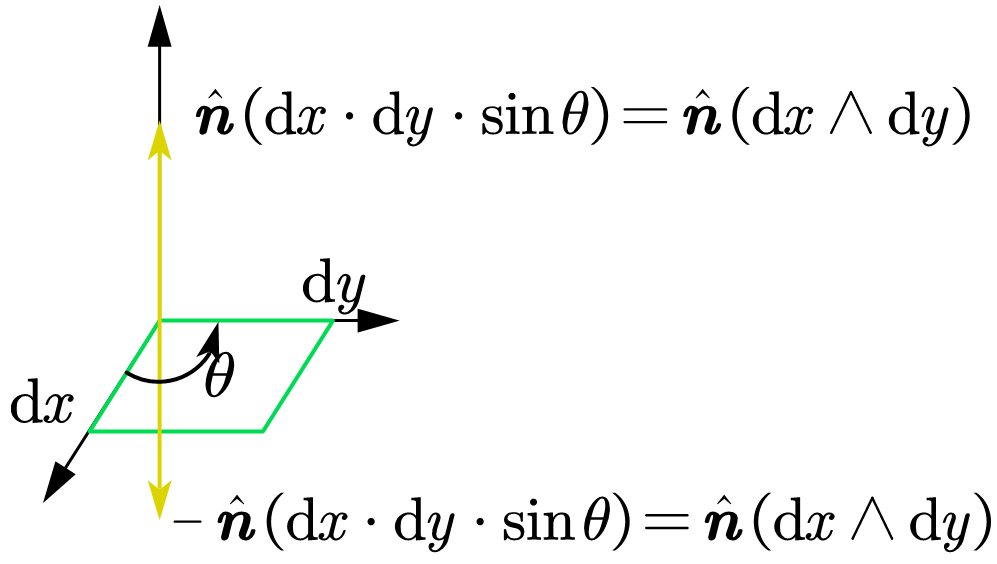外微分

外微分

​ 引入外微分的目的是将Stocks公式，Green公式和Gauss公式用一种方式描述，我们先从Green公式考虑：

对于一个第二型曲面积分：

∬Df(x,y)dxdy=∬D−f(x,y)dydx{\iint }_{D}f\left( {x,y}\right) {dxdy} = {\iint }_{D} - f\left( {x,y}\right) {dydx}

把重积分看作曲面积分的特殊情况 dxdy=−dydx{dxdy}=-{dydx}，如果我们想定义一个统一的形式，我们可以参考叉积的定义，用曲面的法向量方向给积分加上正负号，因此定义楔形积如下：

楔形积

楔积

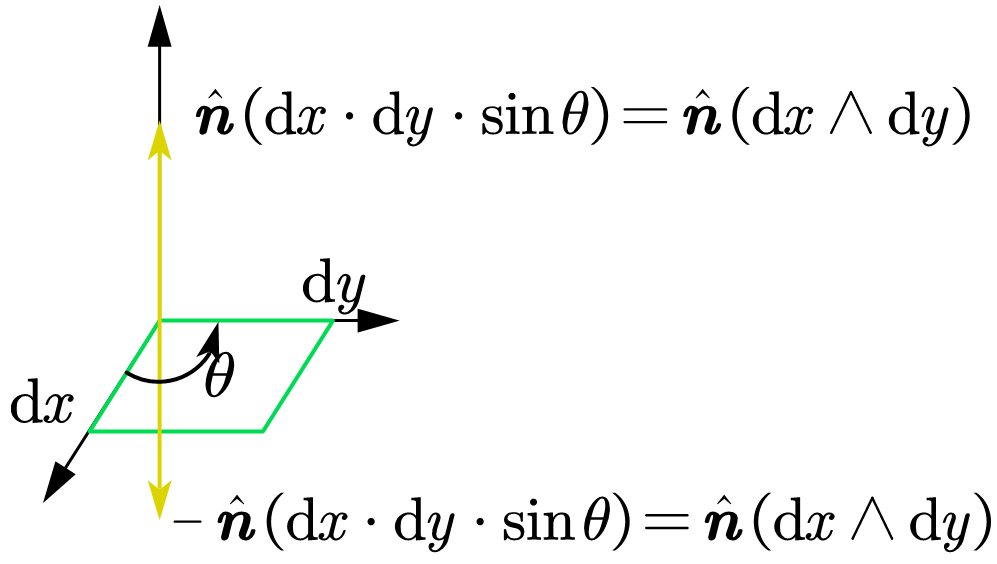
​ 虽然这个理解是用叉积，叉积并不是在所有 nn 为空间都有定义，但是我们可以使用楔积来类似定义这个算子：∧\land，则它有如下性质（反交换律）：

dx∧dy=−dy∧dxdx∧dx=0dx \land dy = - dy \land dx \\ dx \land dx = 0

在三维空间中，楔形积应该满足：

  • dl={dx,dy,dz}d\boldsymbol l=\{dx,dy,dz\} 代表与曲线方向向量同向的矢量线微元
  • dS={dy∧dz,dz∧dx,dx∧dy}d\boldsymbol S=\{dy\land dz,dz\land dx,dx \land dy\} 代表与曲面法向量同向的矢量面微元
  • 因为空间只有 3 维，因此 dV=dx∧dy∧dzdV=dx\land dy \land dz 代表标量体积微元

外微分：

外微分记号dω的含义

总结：如果 $ \omega $ 是一个三元函数 ω=f(x,y,z)\omega =f({x,y,z}) ，那么（这也是我们想要的定义）：

  • ω\omega 被称为「第零次外微分形式」，其微分满足 dω=(∇f)⋅(dl)\mathrm{d}\omega = (\nabla f)\cdot (\mathrm{d}\boldsymbol l)
  • 如果设 F={P,Q,R}\boldsymbol{F} = \{ P,Q,R\} ，ω\omega 是一个一维的微元 ω=F⋅dl=Pdx+Qdy+Rdz\omega = \boldsymbol{F} \cdot \mathrm{d}\boldsymbol{l}= P\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z，那么 ω\omega 被称为「第一次外微分形式」，其微分满足：dω=(∇×F)⋅(dS)\mathrm{d}\omega = (\nabla \times \boldsymbol{F})\cdot (\mathrm{d}\boldsymbol S)
  • 如果设 F={P,Q,R}\boldsymbol{F} =\{P,Q,R\} ω\omega 是一个二维的微元 ω=F⋅dS=P  dy∧dz+Q  dz∧dx+R  dx∧dy\omega = \boldsymbol{F} \cdot \mathrm{d}\boldsymbol{S} = P\mathrm{\;d}y \land \mathrm{d}z + Q\mathrm{\;d}z \land \mathrm{d}x + R\mathrm{\;d}x \land \mathrm{d}y，那么 ω\omega 被称为「第二次外微分形式」，其微分满足：dω=(∇⋅F)⋅(dV)\mathrm{d}\omega =( \nabla \cdot \boldsymbol{F})\cdot(\mathrm{d}V)

可以这么总结： ω\omega 是几次外微分形式，关键看 $\omega =\boldsymbol F \cdot \mathrm{d}X ，，X$ 是几维，外微分就是几次形式，dω\mathrm{d}\omega 被我们称为外微分

外微分的性质

​ 外微分的严谨定义抽象而复杂，我们不给出定义直接给出性质（会用就完啦！）

求外微分就是对每一项的函数全微分，微分之间是外乘积

求一次外微分

α=Pdx+Qdy+Rdzdα=dP∧dx+dQ∧dy+dR∧dz=(∂P∂xdx+∂P∂ydy+∂P∂zdz)∧dx+(∂Q∂xdx+∂Q∂ydy+∂Q∂zdz)∧dy+(∂R∂xdx+∂R∂ydy+∂R∂zdz)∧dz=∂P∂xdx∧dx+∂P∂ydy∧dx+∂P∂zdz∧dx+∂Q∂xdx∧dy+∂Q∂ydy∧dy+∂Q∂zdz∧dy+∂R∂xdx∧dz+∂R∂ydy∧dz+∂R∂zdz∧dz=0−∂P∂ydx∧dy+∂P∂zdz∧dx+∂Q∂xdx∧dy+0−∂Q∂zdy∧dz−∂R∂xdz∧dx+∂R∂ydy∧dz+0=(∂R∂y−∂Q∂z)dy∧dz+(∂P∂z−∂R∂x)dz∧dx+(∂Q∂x−∂P∂y)dx∧dy\alpha = {Pdx} + {Qdy} + {Rdz}\\ {d\alpha } = {dP} \land {dx} + {dQ} \land {dy} + {dR} \land {dz}\\ = \left( {\frac{\partial P}{\partial x}{dx} + \frac{\partial P}{\partial y}{dy} + \frac{\partial P}{\partial z}{dz}}\right) \land {dx} + \left( {\frac{\partial Q}{\partial x}{dx} + \frac{\partial Q}{\partial y}{dy} + \frac{\partial Q}{\partial z}{dz}}\right) \land {dy} + \left( {\frac{\partial R}{\partial x}{dx} + \frac{\partial R}{\partial y}{dy} + \frac{\partial R}{\partial z}{dz}}\right) \land {dz} \\ = \frac{\partial P}{\partial x}{dx} \land {dx} + \frac{\partial P}{\partial y}{dy} \land {dx} + \frac{\partial P}{\partial z}{dz} \land {dx} + \frac{\partial Q}{\partial x}{dx} \land {dy} + \frac{\partial Q}{\partial y}{dy} \land {dy} + \frac{\partial Q}{\partial z}{dz} \land {dy} \\ + \frac{\partial R}{\partial x}{dx} \land {dz} + \frac{\partial R}{\partial y}{dy} \land {dz} + \frac{\partial R}{\partial z}{dz} \land {dz} \\ = 0 - \frac{\partial P}{\partial y}{dx} \land {dy} + \frac{\partial P}{\partial z}{dz} \land {dx} + \frac{\partial Q}{\partial x}{dx} \land {dy} + 0 - \frac{\partial Q}{\partial z}{dy} \land {dz} - \frac{\partial R}{\partial x}{dz} \land {dx} + \frac{\partial R}{\partial y}{dy} \land {dz} + 0 \\ = \left( {\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z}}\right) {dy} \land {dz} + \left( {\frac{\partial P}{\partial z} - \frac{\partial R}{\partial x}}\right) {dz} \land {dx} + \left( {\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}}\right) {dx} \land {dy}

求二次外微分：

β=Adx∧dy+Bdy∧dZ+Cdz∧dxdβ==(∂A∂xdx+∂A∂ydy+∂A∂zdz)∧dx∧dy+(∂B∂xdx+∂B∂ydy+∂B∂zdz)∧dy∧dz+(∂C∂xdx+∂C∂ydy+∂C∂zdz)∧dz∧dx=∂A∂zdz∧dx∧dy+∂B∂xdx∧dy∧dz+∂C∂ydy∧dz∧dx=(∂A∂z+∂B∂x+∂C∂y)dx∧dy∧dz\beta = {Adx} \land {dy} + {Bdy} \land {dZ} + {C} dz \land {dx} \\ {d\beta } = = \left( {\frac{\partial A}{\partial x}{dx} + \frac{\partial A}{\partial y}{dy} + \frac{\partial A}{\partial z}{dz}}\right) \land {dx} \land {dy} + \left( {\frac{\partial B}{\partial x}{dx} + \frac{\partial B}{\partial y}{dy} + \frac{\partial B}{\partial z}{dz}}\right) \land {dy} \land {dz} \\ + \left( {\frac{\partial C}{\partial x}{dx} + \frac{\partial C}{\partial y}{dy} + \frac{\partial C}{\partial z}{dz}}\right) \land {dz} \land {dx} \\ = \frac{\partial A}{\partial z}{dz} \land dx \land dy + \frac{\partial B}{\partial x}{dx} \land {dy} \land {dz} + \frac{\partial C}{\partial y}{dy} \land {dz} \land {dx} \\ = \left( {\frac{\partial A}{\partial z} + \frac{\partial B}{\partial x} + \frac{\partial C}{\partial y}}\right) {dx} \land {dy} \land {dz}

统一三大公式

​ 经过我们上面对外微分的计算，我们可以发现Stokes公式与Guass公式可以用如下的方式统一：

设 Ω\Omega 为 nn 维空间内的一个区域，则 ∂Ω\partial \Omega 为 nn 维空间内的 n−1n-1 维流形，则

∫Ωdω=∫∂Ωω\int_\Omega d \omega = \int_{\partial \Omega}\omega

​ 下面的图有一些小问题，不过能更好地理解三维空间内的外微分：

三维的外微分

庞加莱引理：

Poincaré 引理:

​ 若 ω\omega 为一外微分形式，其微分形式的系数具有二阶连续偏导数，则 ddω=0\mathrm{dd}\omega=0

三维空间下熟悉的例子：

  • 梯度的旋度为0： $ \operatorname{rot\ grad}f = \nabla \times( \nabla f) =\overrightarrow{0}$
  • 旋度的散度为 0：$ \operatorname{div\ rot}\overrightarrow{F} = \nabla \cdot ( \nabla \times \overrightarrow{F}) = 0 $

即梯度无旋、旋度无散