Actor-Critic算法
Actor-Critic
在 REINFORCE 算法中,每次需要根据一个策略采集一条完整的轨迹,并计算这条轨迹上的回报。由于采样方式的方差比较大,学习效率也比较低。我们可以借鉴时序差分学习的思想,使用动态规划方法来提高采样的效率,即从状态 开始的总回报可以通过当前动作的即时奖励 和下一个状态 的值函数来近似估计
演员-评论家算法(Actor-Critic Algorithm)是一种结合策略梯度和时序差分学习的强化学习方法,包括两部分,演员(Actor)和评价者(Critic),跟生成对抗网络(GAN)的流程类似:
- 演员(Actor)是指策略函数 ,即学习一个策略来得到尽量高的回报。用于生成动作(Action)并和环境交互
- 评论家(Critic)是指值函数 ,对当前策略的值函数进行估计,即评估演员的好坏。用于评估Actor的表现,并指导Actor下一阶段的动作
借助于值函数,AC算法可以进行单步更新参数,不需要等到回合结束才进行更新
- Advantage Actor-Critic 叫做
A2C - Asynchronous Advantage Actor-Critic 称为
A3C
Actor-Critic
Q-learning
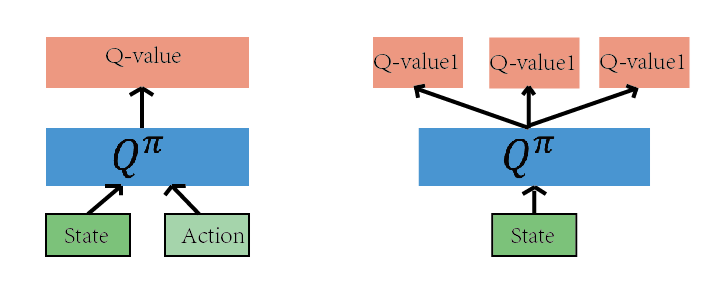
如上图的网络都是为了近似 Q(s,a)函数,有了 Q(s,a),我们就可以根据Q(s,a)的值来作为判断依据,作出恰当的行为。
Q-learning算法决策的依据是 的值。我们可以把这个算法的核心看成一个评论家(Critic),而这个评论家会对我们在当前状态 下,采取的动作 这个决策作出一个评价,评价的结果就是 的值
Q-learning 算法不适合解决连续动作空间的问题。因为如果动作空间是连续的,那么用Q-learning算法就需要对动作空间离散化,就会导致动作空间的维度非常高。Actor-Critic 算法可以认为是 Q-learning 用于处理连续动作空间的算法
Actor Critic
Actor-Critic 是Q-learning 和 Policy Gradient 的结合,为了导出 Actor-Critic 算法,我们先推到 Policy Gradient 算法:
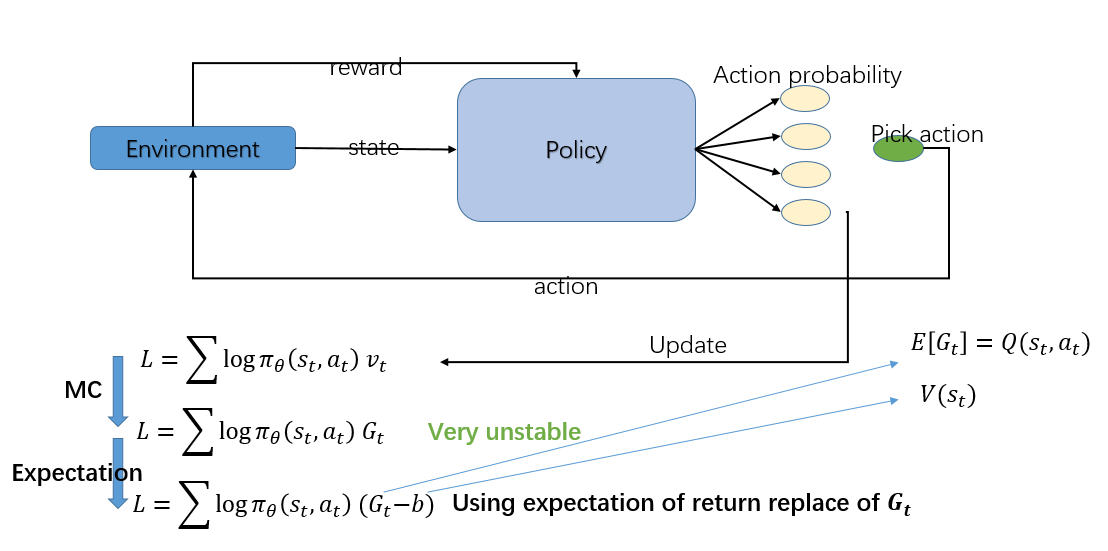
最简单的 Policy Gradient 算法要优化的函数如下:
目标是寻一策略π,最大化期望累积奖励 $ J\left( \pi \right) $ 。策略梯度方法经梯度上升优化此目标函数,每步策略梯度可通过如下简化形式近似:
其中 $\tau $ 代表一个完整轨迹, $ \pi_\theta$ 为策略, 为策略参数,引入Baseline $ b\left(s_t\right)$ 后,公式调整为:
在 $ R_t - b\left( s_t\right)$ 中, 常取 ,则原式即为即优势函数(Advantage) 的一般形式。优势函数衡量采取某动作相较于遵循当前策略的平均效益的优越程度
减Baseline的好处:
-
在策略梯度的上下文中,回报序列的高方差往往源于回报之间的高协方差,如果我们考虑不同时间步 和 的回报 和 ,它们的协方差 描述了两个回报值变动趋势的一致性。当回报序列具有高协方差时,意味着在时间序列上相邻或相隔不远的回报倾向于同时高于或低于它们的平均值,这种同步波动增加了估计梯度时的不确定性,从而增大了方差
-
Baseline的作用:减少回报序列的相关性
引入状态相关的 Baseline 是减小这种相关性的一种有效手段。上面减去 Baseline 的本质是得到了“优势”,这个值反映了相对于策略平均表现的超额回报
-
为何能减少相关性
- 分解信号:通过减去Baseline,将回报分解为策略的平均表现和相对于平均表现的增量部分(即优势)。这种分解有助于分离出那些真正反映策略改进空间的信息,而这些信息通常具有较低的跨时间步相关性
- 增强独立性:优势函数 相比于原始回报 ,在某种程度上更加“独立”于其他时间步的优势函数。这是因为每个时间步的优势值直接反映了相对于策略预期的额外增益,而这种增益受当前决策影响较大,相对独立于其他时间步的决策结果
为什么减去 Baseline 不会对优化过程产生影响?
虽然我们通过减去 Baseline 改变了更新的信号,但优化的目标依然是最大化累积奖励的期望值。减去 Baseline 的操作实质上是改变了解的路径,而非终点。因为优势函数的期望值反映了策略相对于当前策略平均表现的额外收益,优化这个量本质上仍然是为了最大化累积奖励的期望值
因为,故进一步变成:
照上面的式子看来,我们需要两个网络去估计和,但是考虑到贝尔曼方程:
弃掉期望:
在原始的A3C论文中试了各种方法,最后做出来就是直接把期望值拿掉最好,这是根据实验得出来的。
最终的式子为:
这样只需要一个网络就可以估算出V值了,而估算V的网络正是我们在 Q-learning 中做的,所以我们就把这个网络叫做 Critic。这样就在 Policy Gradient 算法的基础上引进了 Q-learning 算法了
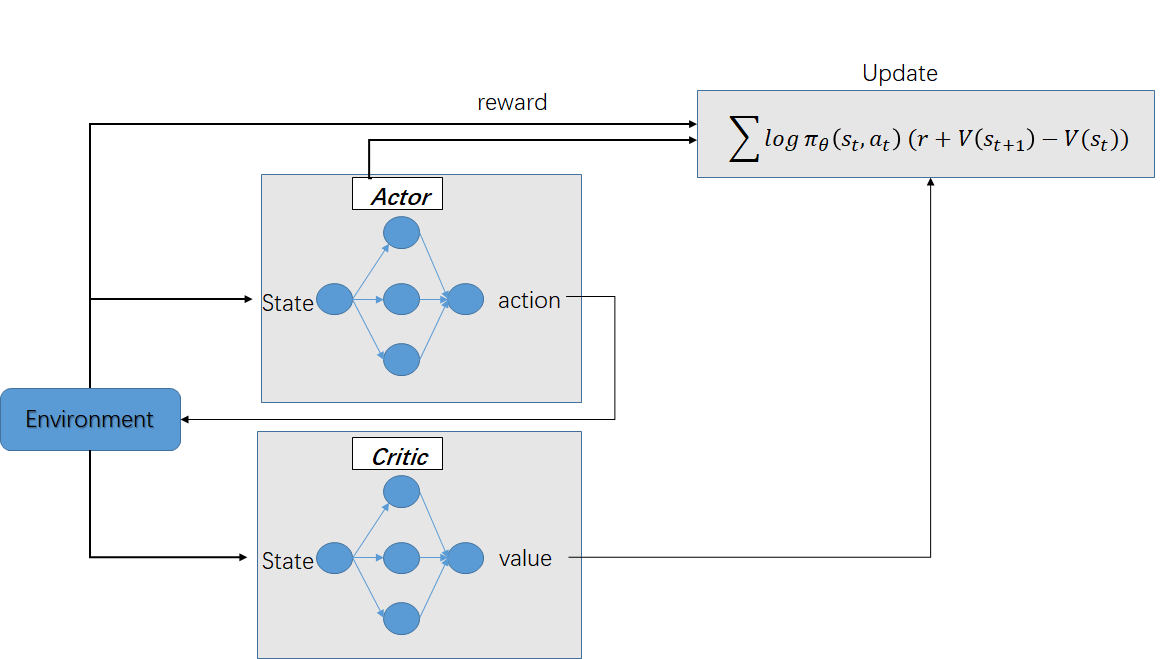
Actor-Critic算法流程
评估点基于TD误差,Critic使用神经网络来计算TD误差并更新网络参数,Actor也使用神经网络来更新网络参数
输入:迭代轮数T,状态特征维度n,动作集A,步长,,衰减因子,探索率, Critic网络结构和Actor网络结构。
输出:Actor网络参数,Critic网络参数
- 随机初始化所有的状态和动作对应的价值Q;
- for i from 1 to T,进行迭代:
- 初始化S为当前状态序列的第一个状态,拿到其特征向量
- 在Actor网络中使用作为输入,输出动作A,基于动作A得到新的状态S’,反馈R;
- 在Critic网络中分别使用,作为输入,得到Q值输出V(S),V(S’);
- 计算TD误差
- 使用均方差损失函数作Critic网络参数w的梯度更新;
- 更新Actor网络参数:
对于Actor的分值函数,可以选择softmax或者高斯分值函数。
Actor-Critic优缺点
优点
- 相比以值函数为中心的算法,Actor - Critic 应用了策略梯度的做法,这能让它在连续动作或者高维动作空间中选取合适的动作,而Q-learning 做这件事会很困难甚至瘫痪。、
- 相比单纯策略梯度,Actor - Critic 应用了Q-learning 或其他策略评估的做法,使得Actor Critic 能
进行单步更新而不是回合更新,比单纯的Policy Gradient 的效率要高。
缺点
- 基本版的Actor-Critic算法虽然思路很好,但是难收敛
目前改进的比较好的有两个经典算法:
- DDPG算法,使用了双Actor神经网络和双Critic神经网络的方法来改善收敛性。
- A3C算法,使用了多线程的方式,一个主线程负责更新Actor和Critic的参数,多个辅线程负责分别和环境交互,得到梯度更新值,汇总更新主线程的参数。而所有的辅线程会定期从主线程更新网络参数。这些辅线程起到了类似DQN中经验回放的作用,但是效果更好。