model_free

model free reinforcement learning

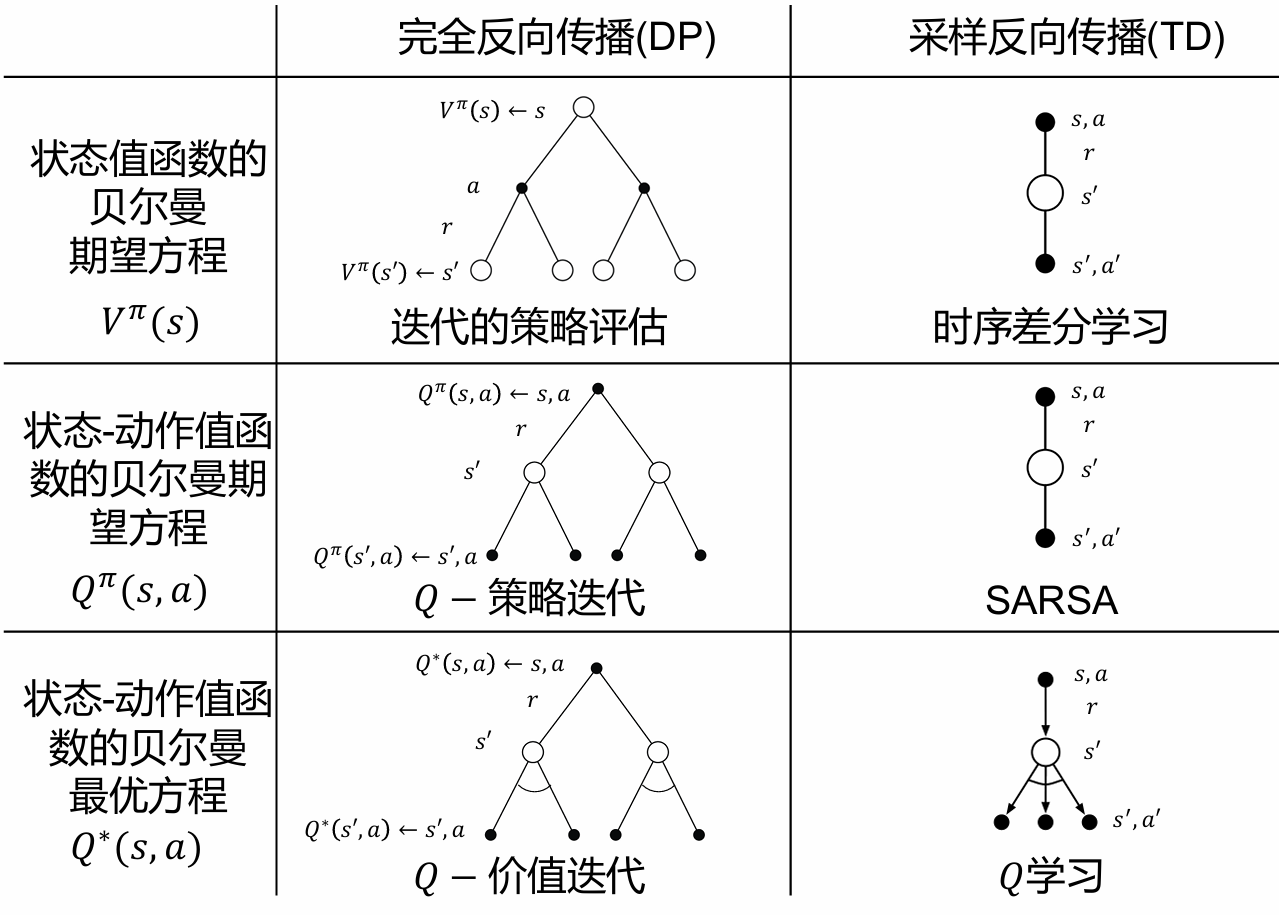
​ Model-Free强化学习（MFRL）的核心在于不依赖环境动态模型的策略学习方法，最优策略的选择为 π(s)=arg⁡max⁡a∈A∑s′Psa(s′)V(s′)\pi(s) = \arg\max_{a \in \mathcal{A}} \sum_{s'}P_{sa}(s')V(s')，但是既然不对环境建模，就无法知道状态转移概率 Psa(s)P_{sa}(s)，因此只能基于 QπQ^\pi 来进行动作的选择，通过直接估计动作值函数Q(s,a)Q(s,a)来指导决策，使得算法在复杂环境中具有更强的适应性：

π(s)=arg⁡max⁡a∈AQ(s,a)\pi(s) = \arg\max_{a \in \mathcal{A}} Q(s,a)

因此，动作值函数的更新，估计就代表着策略的更新，下面举两种 model free 的算法：

On-policy: SARSA

​ On-policy 算法是指使用行为策略（生成数据的策略）与目标策略（优化的策略）完全相同的算法，SARSA 是一种 on-policy 的算法，策略评估和策略改进时采用的策略不同：

  • 策略评估：使用 TD(0)TD(0) 算法更新 Q(s,a):Q(s,a)←Q(s,a)+α(r+γQ(s′,a′)−Q(s,a))Q(s,a): Q(s,a) \leftarrow Q(s,a) + \alpha(r + \gamma Q(s',a')-Q(s,a))
  • 策略改进：ϵ\epsilon-greedy 算法进行策略改进

​ 和前面价值迭代的方式相同，策略评估的方式中，其实包含着策略和 QQ 的耦合更新，每一步更新得到的 QQ 并没有一个策略 π\pi 对应，而是作为一个中间值加速收敛

Q-update

Off-policy: DQN

​ on-policy 的数据问题：on-policy 缺乏训练的数据，每次策略改变之后再之前的数据全部被丢弃，导致数据量不够的问题，往往需要从原先数据内进行重要性采样（variance 很大），为了解决这个问题便有了 Q-learning

​ 什么是 off-policy：off-policy 指的是在数据采集和策略更新所使用的策略不是同一个策略，具体来说分为策略 π\pi 和策略 μ\mu：

  • 目标策略 π(a∣s)\pi(a|s)：进行价值评估（exploitation）(Vπ(s)V^\pi(s) 或 Qπ(s,a)Q^\pi(s,a))
  • 行为策略 μ(a∣s)\mu(a|s)：负责数据采集（exploration）收集数据：{s1,a1,r1,s2,a2,r2,...,sT}∼μ\{s_1, a_1, r_1, s_2, a_2, r_2, ..., s_T\} \sim \mu

off-policy 的好处在于：

  • 平衡探索 (exploration) 和利用 (exploitation)
  • 重用旧策略所产生的经验（增加训练数据）

​ off-policy 算法极大拓宽了强化学习的范围，使用过去积累的数据训练策略，避免高风险场景的频繁试错

Q-learning 中，由 QQ 函数的定义：

Q(st,at)=∑t=0Tγtr(st,at),at∼μ(st)=r(st,at)+γQ(st+1,at+1)\begin{aligned} Q(s_t,a_t) =& \sum_{t=0}^{T} \gamma^t r(s_t,a_t), a_t \sim \mu(s_t) \\ =& r(s_t,a_t) + \gamma Q(s_{t+1},a_{t+1}) \end{aligned}

使用 TD(0)TD(0) 方式进行更新：

Qπ(st,at)=Qπ(st,at)+α(r(st,at)+γQπ(st+1,at+1)−Qπ(st,at))Q^\pi(s_t,a_t) = Q^\pi(s_t,a_t) + \alpha \left(r(s_t,a_t) + \gamma Q^\pi(s_{t+1},a_{t+1}) - Q^\pi(s_t,a_t)\right)

​ 为什么这样更新不需要重要性采样？原因在于策略 μ\mu 只影响当前 sts_t 状态下采用 ata_t 动作，后续的 QπQ^\pi 值仍然是有策略 π\pi 来决定的（历史信息），因此不需要使用重要性采样

我们让目标策略 π\pi 为最优策略，则 Q-learning 的更新方式变为：

Qπ(st,at)←Qπ(st,at)+α(r(st,at)+γQπ(st+1,at+1)−Qπ(st,at))=Qπ(st,at)+α(r(st,at)+γQπ(st+1,arg⁡max⁡at+1′Q(st+1,at+1′))−Qπ(st,at))=Qπ(st,at)+α(r(st,at)+γarg⁡max⁡at+1′Qπ(st+1,at+1′)−Qπ(st,at))\begin{aligned} Q^\pi(s_t,a_t) \leftarrow & Q^\pi(s_t,a_t) + \alpha \left(r(s_t,a_t) + \gamma Q^\pi(s_{t+1},a_{t+1}) - Q^\pi(s_t,a_t)\right) \\ =& Q^\pi(s_t,a_t) + \alpha \left(r(s_t,a_t) + \gamma Q^\pi(s_{t+1},\arg\max_{a_{t+1}'} Q(s_{t+1}, a_{t+1}')) - Q^\pi(s_t,a_t)\right) \\ =& Q^\pi(s_t,a_t) + \alpha \left(r(s_t,a_t) + \gamma \arg\max_{a_{t+1}'} Q^\pi(s_{t+1}, a_{t+1}') - Q^\pi(s_t,a_t)\right) \end{aligned}

​ 注意 off-policy 上面的理解只对于策略相差不大（采样策略和更新策略）的情况下，如果策略相差过大 QQ-learning 的算法是十分低效的

重要性采样的规避机制

​ Off-Policy 方法通过价值函数的策略一致性规避了传统重要性采样的需求：

Qπ(st,at)=Eμ[r+γQπ(st+1,at+1)∣st,at]Q^\pi(s_t,a_t) = \mathbb{E}_\mu\left[r + \gamma Q^\pi(s_{t+1},a_{t+1}) | s_t,a_t\right]

​ 关键在于目标策略 π\pi 主导后续状态-动作对的选择，使得期望计算不依赖行为策略 μ\mu 的采样分布。这种特性使得 Q-learning 在策略差异较小时效率显著提升，但在策略差异过大时可能面临收敛性挑战

应用场景对比分析

特性 On-Policy Off-Policy
数据效率 低（需持续交互） 高（可复用数据）
探索安全性 风险较高 可控（分离策略）
算法复杂度 较低 较高
典型应用 在线实时控制 推荐系统、医疗决策

illustration

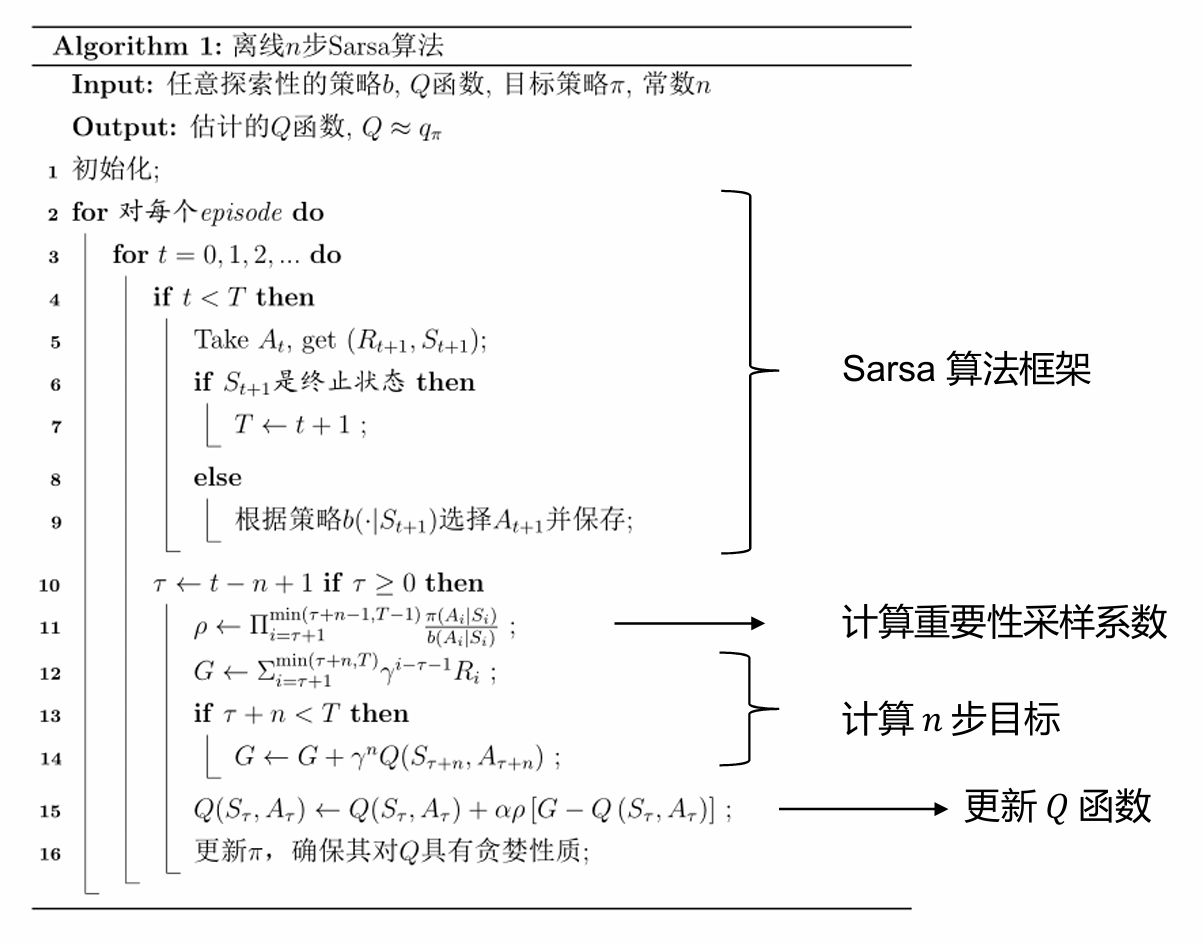
Off-policy & Importance Sampling

​ 前面我们说过，任何 on-policy 算法都可以使用 off-policy 方式进行学习，SARSA 也不例外，我们可以将多步 SARSA 使用 off-policy 方式进行学习，同时引入重要性采样（需要重要性采样的原因在于多步 SARSA + off-policy）：

SARSA+off-policy