普通的 DQN 算法通常会导致对Q 值的过高估计(overestimation)。原因在与 Q 网络的自举(bootstrapping):
传统 DQN 优化的 TD 误差目标为:
r + γ max a ′ ∈ A Q w − ( s ′ , a ′ ) r+\gamma \max_{a'\in A}Q_{w^-}(s',a')
r + γ a ′ ∈ A max Q w − ( s ′ , a ′ )
其中,max a ′ Q w − ( s ′ , a ′ ) \max_{a'}Q_{w-}(s',a') max a ′ Q w − ( s ′ , a ′ ) w − w^- w − max \max max
选取状态 s ′ s' s ′ a ∗ = arg max a ′ Q a^*=\arg \max_{a'}Q a ∗ = arg max a ′ Q
再计算该动作对应的价值 Q w − ( s ′ , a ′ ) Q_{w^-}(s', a') Q w − ( s ′ , a ′ )
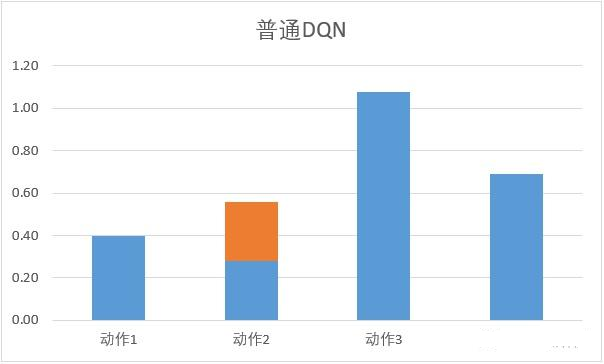
当这两部分共同采用同一套 Q 网络的时候,每次得到的都是神经网络中估算所有动作状态的最大值 ,考虑神经网络会不断累计正误差,DQN 的过高估计问题会非常严重,本质上的原因在于:
探索不足:探索不足导致产生的样本无法反应出概率分布: π : p ( s ′ , r ∣ s , a ) \pi:p\left( s',r {\mid} s,a \right) π : p ( s ′ , r ∣ s , a )
值函数存在方差: Q ( s , a ) Q(s,a) Q ( s , a )
贪心思想将高估的值进行了传递 :训练过程中,实际的 Q ( s ′ , a ′ ) Q\left( s',a' \right) Q ( s ′ , a ′ ) Q ∗ ( s ′ , a ′ ) Q^{*}\left( s',a' \right) Q ∗ ( s ′ , a ′ ) Q ( s , a ) Q(s,a) Q ( s , a ) s ′ s' s ′ max a ′ Q ( s ′ , a ′ ) \max_{a'}Q\left( s',a' \right) max a ′ Q ( s ′ , a ′ )
为了解决这一问题,Double DQN 算法提出利用两套独立训练的神经网络来估算 max a ‘’ Q ∗ ( s ′ , a ′ ) \max\limits_{ a‘’}Q^*\left(s', a' \right) a ‘ ’ max Q ∗ ( s ′ , a ′ ) 利用 一套神经网络 Q ω Q_{\omega} Q ω Q a r Q_{ar} Q a r 。这样即使其中一套神经网络的某个动作存在比较严重的过高估计问题,由于另一套神经网络的存在,这个动作最终使用的 Q Q Q
我们设选取动作网络参数为 w w w w − w^- w −
r + γ Q w − ( s ′ , arg max a ′ Q w ( s ′ , a ′ ) ) r+\gamma Q_{w^-}(s', \arg\max_{a'}Q_{w}(s', a'))
r + γ Q w − ( s ′ , arg a ′ max Q w ( s ′ , a ′ ) )
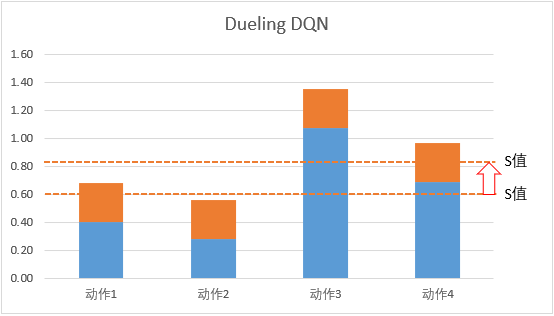
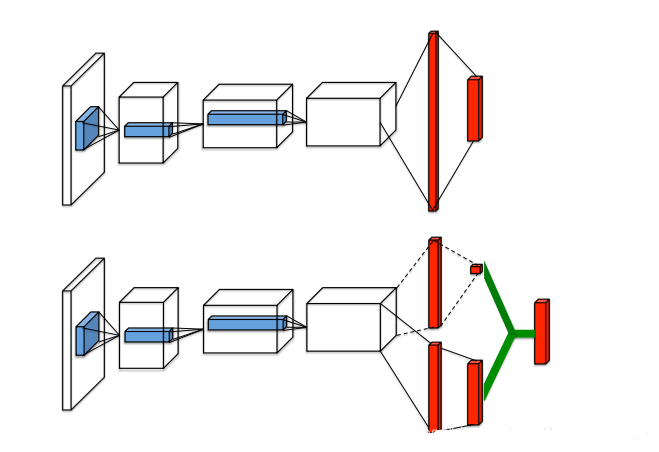
Dueling DQN是 DQN的另一种改进算法,它在传统 DQN 的基础上只进行了微小的改动,但能大幅提升 DQN的表现
它从另外一个方面考虑 DQN 的问题:每次更新 Q 网络的时候,我们只是对网络中的最大值进行反向传播,而不管其他的 Q 值,这导致不同动作的 Q 值可能相差过大:
因此在 Dueling DQN 中,引入优势函数的概念:
将动作价值函数 Q Q Q V V V A A A A ( s , a ) = Q ( s , a ) − V ( s ) A(s,a)=Q(s,a)-V(s) A ( s , a ) = Q ( s , a ) − V ( s )
因此 Q 网络被建模为:
Q η , α , β ( s , a ) = V η , α ( s ) + A η , β ( s , a ) Q_{\eta, \alpha, \beta}(s,a)=V_{\eta, \alpha}(s)+A_{\eta, \beta}(s,a)
Q η , α , β ( s , a ) = V η , α ( s ) + A η , β ( s , a )
对于公式 Q η , α , β ( s , a ) = V η , α ( s ) + A η , β ( s , a ) Q_{\eta,\alpha,\beta}\left( s,a\right) = V_{\eta,\alpha}\left( s \right) + A_{\eta,\beta}\left( s,a\right) Q η , α , β ( s , a ) = V η , α ( s ) + A η , β ( s , a ) V V V A A A Q Q Q V V V C C C A A A C C C Q Q Q 导致了训练的不稳定性 。为了解决这一问题,Dueling DQN 强制最优动作的优势函数的实际输出为 0 , 即:
Q_{\eta,\alpha,\beta}\left(s,a \right) = V_{\eta,\alpha}\left( {s} \right) + A_{\eta,\beta}\left( {s}, {a} \right) {-} {\max}\limits_{ {d}}A_{\eta,\beta}\left( {s}, a' \right)
此时 V ( s ) = max a Q ( s , a ) V(s) = \max_aQ(s,a) V ( s ) = max a Q ( s , a ) V V V
Q η , α , β ( s , a ) = V η , α ( s ) + A η , β ( s , a ) − 1 ∣ A ∣ ∑ d A η , β ( s , a ′ ) Q_{\eta,\alpha,\beta}\left(s,a\right) = V_{\eta,\alpha}\left( s\right) + A_{\eta,\beta}\left(s, a \right) - \frac{1}{|A|}\sum_dA_{\eta,\beta}\left(s,a' \right)
Q η , α , β ( s , a ) = V η , α ( s ) + A η , β ( s , a ) − ∣ A ∣ 1 d ∑ A η , β ( s , a ′ )
此时 V ( s ) = 1 ∣ A ∣ ∑ d Q ( s , a ′ ) V(s) = \frac{1}{|A|}\sum_d Q( s,a') V ( s ) = ∣ A ∣ 1 ∑ d Q ( s , a ′ )
无论是 Double DQN 还是 Dueling DQN,他们都是通过优化神经网络结构的方式来改进 DQN 中 Q Q Q Q Q Q Q Q Q
一些工具类:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class RelayBuffer (object ):def __init__ (self, max_length ):def add (self, state, action, reward, next_state, done ):def sample (self, batch_size ):return random.sample(self.buffer, batch_size)def size (self ):return len (self.buffer)class Qnet (nn.Module):def __init__ (self, state_dim, hidden_dim, action_dim ):super ().__init__()def forward (self, x ):return xclass VAnet (torch.nn.Module):def __init__ (self, state_dim, hidden_dim, action_dim ):super (VAnet, self).__init__()1 )def forward (self, x ):1 , keepdim=True )return Q
实现与训练代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 device = torch.device("cuda" if torch.cuda.is_available() else "cpu" )class DQN (object ):def __init__ (self, state_dim, hidden_dim, action_dim, learning_rate, gamma, epsilon, target_update, type ='ValillaDQN' ):if type == 'DuelingDQN' :elif type == 'ValillaDQN' or 'DoubleDQN' :else :assert False , 'DQN type error' 0 type = type def take_action (self, state ):""" 实现epsilon-greedy策略 """ if np.random.random() < self.epsilon:else :float , device=device)return actiondef max_q_value (self, state ):float , device=device)return self.q_net(state).max ().item()def update (self, transition ):""" train 函数中的内部部分 """ float , device=device)1 , 1 )float , device=device).reshape(-1 , 1 )float , device=device)float , device=device).reshape(-1 , 1 )1 , actions)if self.type == 'DuelingDQN' or 'ValillaDQN' :max (self.q_net(states), dim=1 , keepdim=True )elif self.type == 'DoubleDQN' :1 , keepdim=True )1 , max_action)1 - dones)if self.count % self.target_update == 0 :0 1 1e-2 200 128 0.98 0.01 50 5000 1000 64 'Pendulum-v1' 0 ]11 def dis_to_con (discrete_action, env, action_dim ): 0 ] 0 ] return action_lowbound + (discrete_action / (action_dim - 1 ) * (action_upbound - action_lowbound))def train_DQN (agent, env, num_episodes, replay_buffer, minimal_size, batch_size ):0 for i in range (10 ):with tqdm(total=int (num_episodes / 10 ),'Iteration %d' % i) as pbar:for i_episode in range (int (num_episodes / 10 )):0 False while not done:0.005 + max_q_value * 0.995 if replay_buffer.size() > minimal_size:if (i_episode + 1 ) % 10 == 0 :'episode' :'%d' % (num_episodes / 10 * i + i_episode + 1 ),'return' :'%.3f' % np.mean(return_list[-10 :])1 )return return_list, max_q_value_list