奈奎斯特判据推导
对于线性定常系统,我们之前最初判断稳定性的方式是:判断闭环传递函数所有根(即所有闭环极点)的实部是否全部为负。奈奎斯特判据的目标是,通过一种共性映射将原复平面(记为 s 平面)映射到新的平面(记为 F 平面),通过辐角原理在新的复平面上研究闭环极点的新位置反推原复平面内闭环极点的位置情况
辐角原理
设复平面上的回路 Γs 的内部为 I(Γs),若 F(s) 在 I(Γs) 中除了有限个极点外处处解析(亚纯函数),且 F(s) 在 Γs 上解析且不为 0,则
P(F,Γs)−Z(F,Γs)=2π1ΔargF(s)
其中 P(F,Γs),Z(F,Γs) 分别为 F(s) 在 I(Γs) 中的极点(pole)与零点(zero)个数,ΔargF(s) 是 s 沿顺时针方向旋转一周时 F(s) 辐角的增量
证明:
Ln f(s) = ln\abs{f(s)}+i\arg f(s)\\arg f(s) = \arg Ln f(s) \\
\Rightarrow \Delta \arg f(s) = \Delta \arg Ln f(s)\\
\frac{}{}
奈奎斯特稳定性判据
我们希望选择 F(s) 才能与系统稳定性结合,我们选泽反馈系统的 F(s)=1+G(s)H(s),可以发现:
- F(s) 的零点为闭环传递函数的极点
- F(s) 的极点为开环传递函数(加上反馈传递函数)的极点
则闭环系统稳定的充要条件为 F(s) 零点均在 s 平面的左半平面
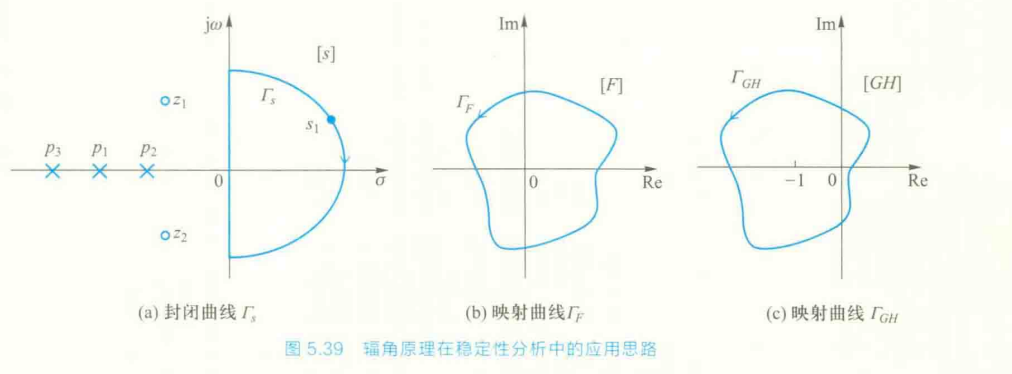
若我们将 s 平面的闭合曲线取为包围整个右半平面的圆弧(称为D型围线,我们可以把D型围线取得足够大让它包围所有 F(s) 的零极点),设 F(s) 在右半平面内极点数和零点数为 P,Z,则:
当 s 平面上沿 Γs 顺时针方向转一周时,在 F 平面上 ΓF 绕原点逆时针旋转的周数 N 等于 s 平面上封闭曲线 Γs 包含 F(s) 的极点数 P 和零点数 Z 之差,即 N=P−Z
而 G(s)H(s) 其实就是我们的幅相曲线,所以我们把问题化为在 F 平面内 ΓGH 绕点 (−1,0) 的圈数 N:
-
如果 G(s)H(s) 的变化曲线 ΓGB 绕 (−1,0) 顺时针旋转,则 N<0 ;
-
如果 G(s)H(s) 的变化曲线 ΓGR 不包围 (−1,0) 点,则 N=0 ;
-
如果 G(s)H(s) 的变化曲线 ΓGH 穿过 (−1,0) 点,即 G(s)H(s)=−1,说明 F(s) 的 变化曲线 ΓF 穿过原点,即 F(s)=0,则封闭曲线 Γs 穿过了 F(s) 的零点,也就意味着封闭曲线 Γs 穿过了原闭环传递函数的极点
映射
我们的幅相曲线定义是代入 s=jw 让 w 从0变为无穷画出来的曲线,但是我们需要D型围线从虚轴的负无穷到虚轴的正无穷,这里的幅相曲线显然是不满足的,不过考虑到幅相曲线的实部是关于 w 的偶函数,虚部是关于 w 的奇函数,因此在 s 平面中从虚轴的 −∞∼0 对应的曲线就是 F 平面中原幅相曲线的沿实轴的对称曲线(注意方向也对称),于是现在唯一的问题就是从D型围线中从虚轴的正无穷重新回到虚轴的负无穷对应的曲线:
第三段无穷半径的圆弧:
由于选取的旋转方向为顺时针旋转,因此我们设第三段曲线方程为 s=limR→∞Re−jθ,其中 θ:−90°→90°,由于:
G(s)H(s)R→∞=ansn+an−1sn−1+⋯+a0bmsm+bm−1sm−1+⋯+b0=R→∞limanbmRm−nej(n−m)θ={anbm n=m0 n>m
因此 s 平面内无穷大半径的弧对应映射到 F 平面内就是一个点,因此我们就可以不管在 F 平面内考虑第三段的对应曲线!
s 平面内虚轴上存在极点的讨论:
我们前面提到过,应用辐角原理需要曲线上解析,但是实际上我们没有任何限制说D型围线上不许出现极点,因此我们讨论两种 F 不解析的特殊情况:
s 平面原点处存在开环极点:
此时可以发现开环传递函数有 v 个积分环节,我们将封闭曲线稍微变形一下让它绕过原点极点(称它为增补段):s=limr→0reiθ,θ:−90°→90°,则增补段在 F 平面内映射为:
G(s)H(s)r→0=sv(ansn−v+⋯+av)K(b+msm+bm−1sm−1+⋯+b0)=∞e−jvθ
因此在原开环传递函数存在积分环节的时候,F 平面内需要增加上半径为无穷大的圆弧,且在 w 从 0− 变到 0+ 的时候圆弧顺时针绕原点旋转 vπ
s 平面虚轴上存在成对开环极点:
同理分析可得:增补段在 F 平面内对应曲线为无穷大的圆弧,且在 w 从 d− 变到 d+ 的时候圆弧顺时针绕原点旋转 vπ
可以得出结论:s 平面虚轴上有多少个极点对应就要画多少个半径为无穷的圆弧增补段
奈奎斯特判据定理:
奈奎斯特稳定判据 (Nyquist stability criterion) : 对于反馈控制系统,设其开环传递函数为 G(s)H(s),P 为位于 s 平面右半平面的 G(s)H(s) 的极点数,N 为 G(s)H(s) 的奈氏曲线(包括增补段的映射曲线)逆时针方向包围 (−1,0) 的次数,若奈氏曲线不穿过 (−1,0) 点,则有下面结论:
-
闭环系统稳定的充分必要条件是 P=N
-
若 P−N>0 ,则闭环系统不稳定,不稳定根 (右半平面的根) 的个数为 Z=P−N
若奈氏曲线穿过 (−1,0) 点,闭环极点存在纯虚根或者零根
对于最小相位系统,它的定义是 s 平面右半平面没有零极点的系统,因此如果对最小相位系统使用奈奎斯特判据,P 就自动等于0了
