n维欧拉公式

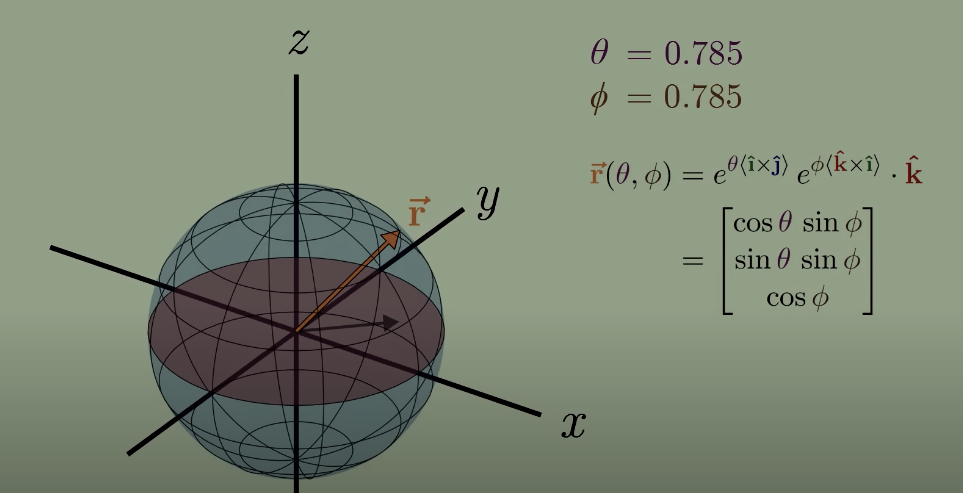
欧拉公式在n维的推广

我们知道 $e^{z} = e^r(cos \theta + sin\theta)$ 为最熟悉的欧拉公式形式，而复数的表示可以用二元的矩阵取代，因此我们可以将复数形式的欧拉公式改写为矩阵形式，因此很自然的一个想法是，这个公式是否能推广到 $n$ 维欧式空间

欧拉公式的意义

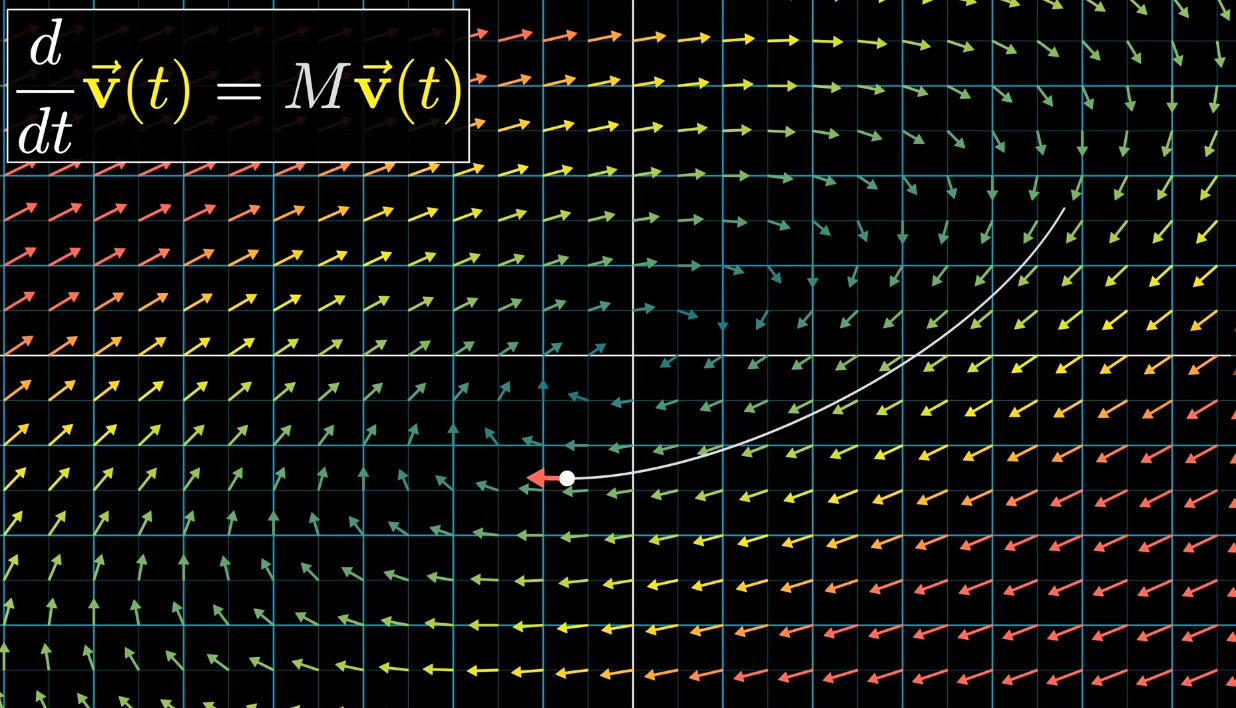
以一个线性微分方程组为例：

\left\{\begin{matrix} \frac{d}{dt}x_{1}(t) = a_{11}x_{1}(t) + a_{12}x_{2}(t) + {\cdots} + a_{1n}x_{n}(t) \\ \frac{d}{dt}x_{2}(t) = a_{21}x_{1}(t) + a_{22}x_{2}(t) + {\cdots} + a_{2n}x_{n}(t) \\ {\cdots} \\ \frac{d}{dt}x_{n}(t) = a_{n1}x_{1}(t) + a_{n2}x_{2}(t) + {\cdots} + a_{nn}x_{n}(t) \end{matrix} \right.

可以把它等价地写为 $\frac{d}{dt}\boldsymbol x(t) = A\boldsymbol x(t)$ ，它的解就像普通微分方程一样： $\boldsymbol x(t) = e^{\boldsymbol At}\boldsymbol x(0)$ ，它的几何意义是一个 $n$ 维向量在空间内的运动情况，我们把 $\boldsymbol x$ 视为运动轨迹，则 $\boldsymbol A$ 则视为对空间内的位置到对应的速度的变换：

A的含义

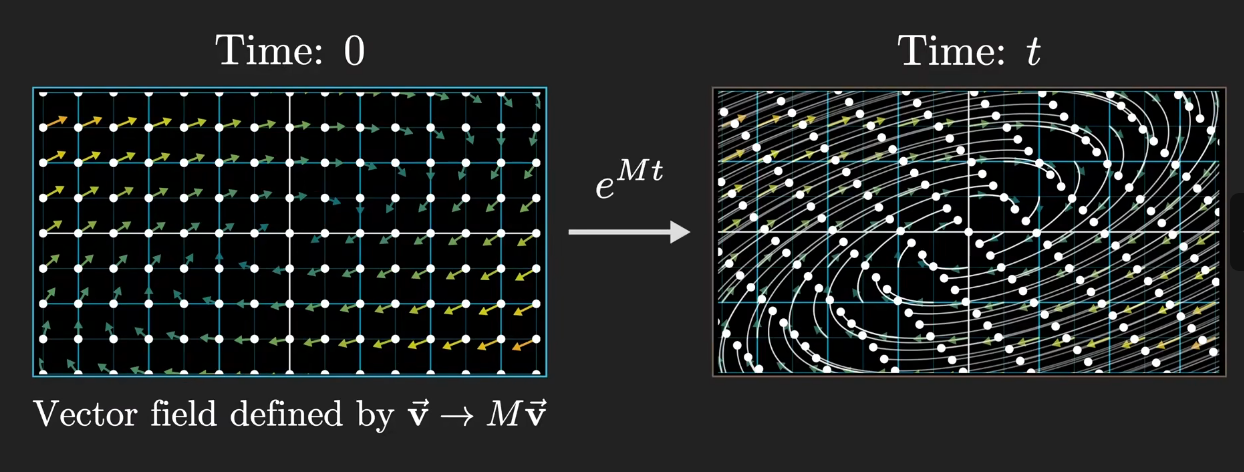
该方程的解 $e^{\boldsymbol At}$ 视为让一个初始值沿着这个场运动 $t$ 时间（它仍然是一个矩阵，还是对空间的一个变换）：

e^T

如果能写出沿某个平面的沿着某个东西旋转的速度场，那么我们是否能利用这个公式来拓展我们的欧拉公式，让他描绘出旋转的过程？

令 $R = \left[ \begin{array}{c} 0, -1\\ 1,\ 0\\ \end{array} \right]$ ，则 $\boldsymbol R$ 代表在这个空间逆时针旋转 $90\degree$ 的速度场， $e^{\boldsymbol Rt}$ 就是旋转矩阵：

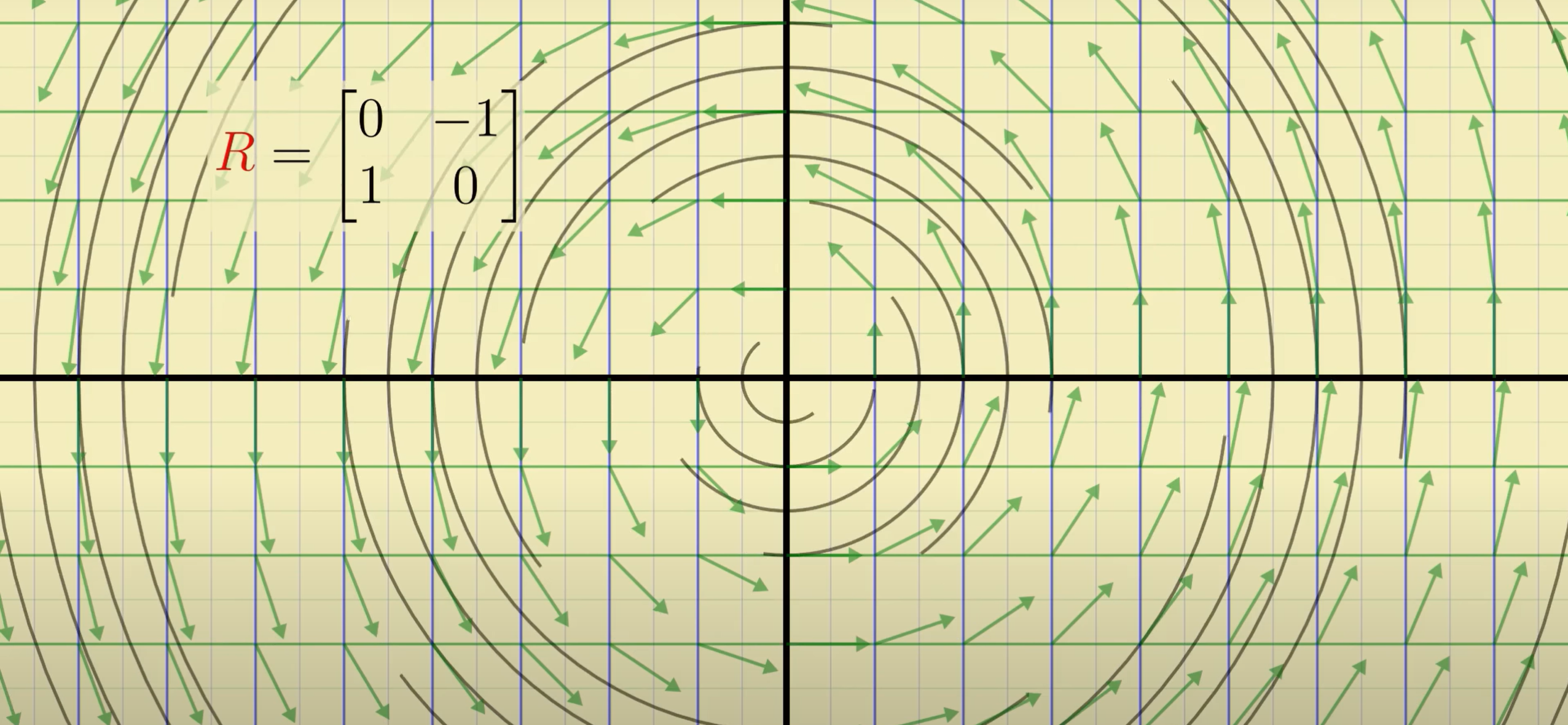
那么按理来说 $e^{\boldsymbol Rt}$ 具有周期性，我们用数学的方式论证一下：

由于 $R$ 的特殊性：

\boldsymbol{R}^4=\left[ \begin{matrix} 0& -1\\ 1& 0\\ \end{matrix} \right] ^4=\left[ \begin{matrix} -1& 0\\ 0& -1\\ \end{matrix} \right] ^2=\boldsymbol{I}

我们可以按照矩阵指数函数的定义直接展开：

e^{\boldsymbol{Rt}}=\sum_{n=0}^{\infty}{\frac{\boldsymbol{R}^n}{n!}t^n} =e^{\boldsymbol{Rt}}=\sum_{n=0}^{\infty}{\frac{\boldsymbol{R}^n}{n!}t^n} \\ =\sum_{n\equiv 0\left( mod4 \right)}{\frac{1}{n!}\left[ \begin{matrix} t^n& 0\\ 0& t^n\\ \end{matrix} \right]}+\sum_{n\equiv 1\left( mod4 \right)}{\frac{1}{n!}\left[ \begin{matrix} 0& -t^n\\ t^n& 0\\ \end{matrix} \right]}+\sum_{n\equiv 2\left( mod4 \right)}{\frac{1}{n!}\left[ \begin{matrix} -t^n& 0\\ 0& -t^n\\ \end{matrix} \right]}+\sum_{n\equiv 3\left( mod4 \right)}{\frac{1}{n!}\left[ \begin{matrix} 0& t^n\\ -t^n& 0\\ \end{matrix} \right]} \\ =\left[ \begin{matrix} 1-\frac{t^2}{2}+\frac{t^4}{4!}-\cdots& -t+\frac{t^3}{3!}-\frac{t^5}{5!}+\cdots\\ t-\frac{t^3}{3!}+\frac{t^5}{5!}-\cdots& 1-\frac{t^2}{2}+\frac{t^4}{4}-\cdots\\ \end{matrix} \right] =\left[ \begin{matrix} \cos t& -\sin t\\ \sin t& \cos t\\ \end{matrix} \right]

这不就是线性代数里面熟悉的旋转矩阵吗（其实这也是二维的欧拉公式），有了这个理解，我们可以继续理解我们的高维欧拉公式

高维欧拉公式

很遗憾的是，高维的欧拉公式只能规定在某一个平面里面旋转 $n$ 维向量，由于复平面的特殊性，我们在复平面内往往意识不到这一点

我们以三维空间为例，设 $\boldsymbol{\vec{u}\ \vec{v}}$ 为相互正交的单位向量（这样可以先不考虑它的伸缩性），考虑 $\boldsymbol{\vec{w}}=\boldsymbol{\vec{u} \times \vec{v}\ \ \ \ \vec{r}'=\vec{w} \times \vec{r}}$ （理解它的几何含义），这样就能把 $\boldsymbol {\vec{r}}$ 在 $\boldsymbol{\vec{u}\ \vec{v}}$ 平面内顺时针旋转 $\pi/2$ ，我们发现三重叉积就是我们想要的旋转，下面我们用矩阵的语言描述它：