Rewrite the Stars论文精读
Why do element-wise mutiplication work?
我们常常注意到在神经网络中,element-wise multiplication 往往能够取得很好的效果。之前不同领域中文章往往也应用了这一点并且提出了各自的概念或解释(例如gating mechanism,high-order, modulation mechanism, visual-attention等等),但是往往都是比较直觉的。 这篇文章主要尝试去真正的解释为什么神经网络中element-wise multiplication效果好: 因为在神经网络中element-wise multiplication起到了一个多项式核函数的作用-将特征隐式的映射到一个高维的非线性的空间上,从而增大了模型的表达能力,提高performance。当我们意识到element-wise multiplication其实起到了核函数的作用时,我们其实有很多可以后续做的尝试的很有趣的事情(例如完全没有激活函数的DNN等)
Introduction
我们首先经验主义地来分析下star会带来什么好处(本文把 element-wise multiolication 称为 star operation)。 论文中简化了 FocalNet/VAN 等设计,抽象出下图一个简单的 Demo block ,然后堆这个block形成一个网络叫做 DemoNet ,在 ImageNet 上来比较 star 和 sum 的效果区别。在没有任何其他因素的影响下,我们发现star取得的效果远远高于sum,而且效果好得很明显,能够在ImageNet上比sum高出2-6个点!(⚠️非常夸张)
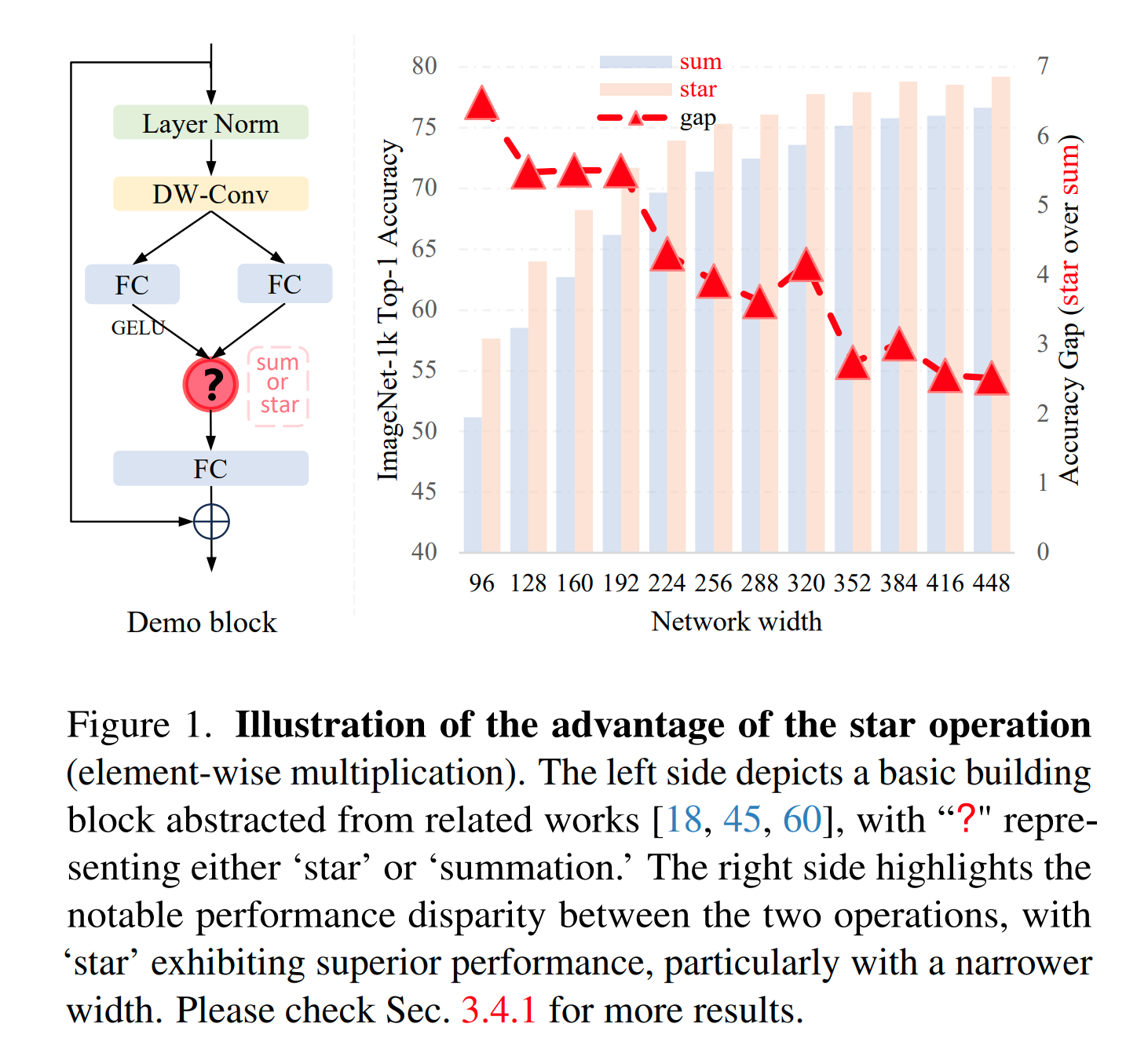
原因解析:
在单层神经网络中,star operation 操作可以写为 ,代表两个线性特征的融合为一个新的特征,为了简单起见,可以把偏置项写入输入,即用如下记号:
为了简化分析,下面假设形状:
其中 为隐藏层维度, 为输入数据维度, 为输入数据长度,则 star operation 可以写为:
注意这里的上标不代表着几次方,而是代表着第几个数(原论文记号太阴间了), 的表达式如下:
每一项都代表着 的非线性组合的系数,总共有 项,即当我们组合用了 star 和全连接层时,其实一个 维的特征中任意两维都相乘组合成了一个新的维度,和原本的 维中任意一维都是线性无关的。那么这不就是核函数(并且是多项式核函数)的核心思想吗:低维映射到高维非线性特征提高表达力!这也部分印证了在上图中随着网络宽度增加,element-wise multiplication 和 sum之间的效果差异逐渐减小的现象。而且这只是一层网络可以将 维空间隐性的投影到 维上,当堆叠多层时候,几乎可以达到无限维!例如对于一个10层128维宽的网络,最后能够实际达到大约90^1024维!
进一步的证明:
为了进一步说明 star operation 引入非线性的影响。论文中把 DemoNet 网络中唯一的激活函数扔了,使得整个网络完全不包含任何非线性(忽略layer norm)
用sum时候,整个网络效果下降巨大,但是用star时候,几乎没有下降。论文中举了很多实验更充分地说明了这一点
可视化验证:
论文进一步做了一个月牙形 点的决策面的实验, 实验发现, element-wise multiplication 网络的决策面和 polynomial SVM 的很像,而与 Gaussian SVM 决策面差距很大。进一步从视觉上验证了分析:

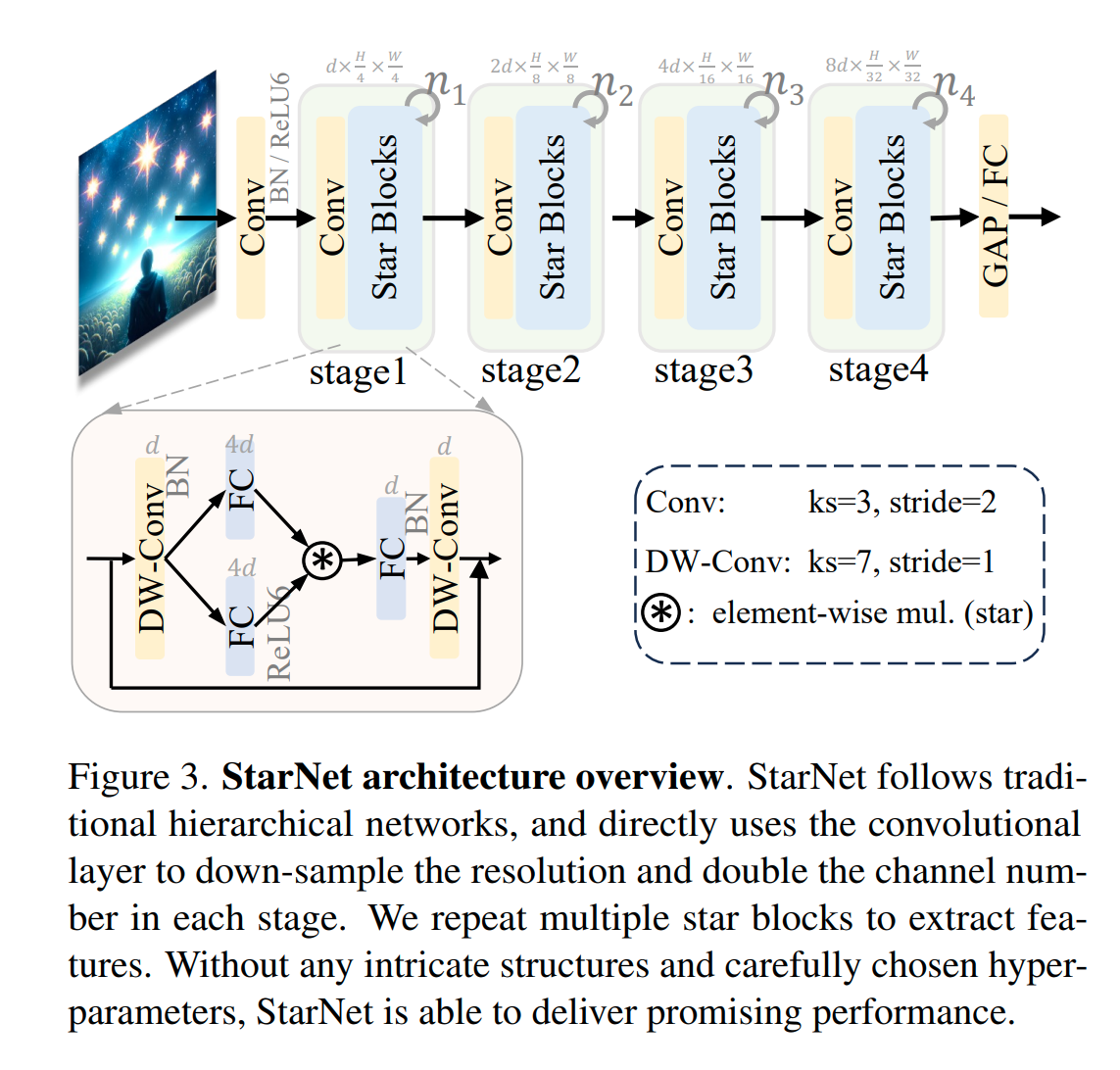
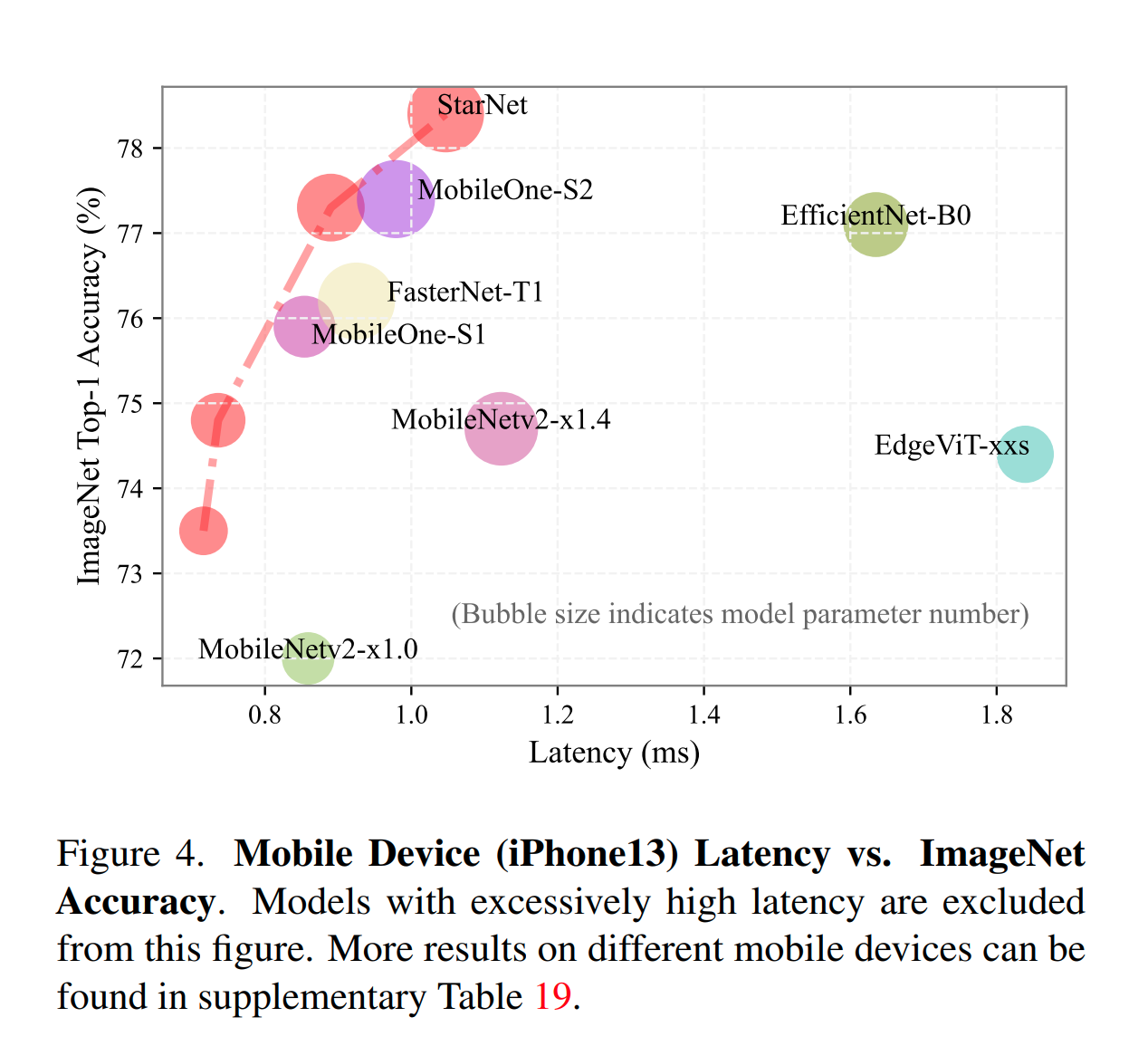
Proof-of-concept应用:
最后,联系到 Kernel trick 的意义和应用,论文尝试了一个极其简单的的efficient网络:StarNet,几乎朴素到不能再朴素, 却能够取得非常惊艳的效果, 也进一步说明的 element-wise multiplication 的应用价值: