Manba论文解读

​ 自 2017 年被提出以来，Transformer 已经成为 AI 大模型的主流架构，但随着模型规模的扩展和需要处理的序列不断变长，Transformer 的局限性也逐渐凸显。一个很明显的缺陷是：Transformer 模型中自注意力机制的计算量会随着上下文长度的增加呈平方级增长，比如上下文增加 32 倍时，计算量可能会增长 1000 倍，计算效率非常低。

​ 而就在最近，Mamba 的架构似乎打破了这一局面。与类似规模的 Transformer 相比，Mamba 具有 5 倍的吞吐量，而且 Mamba-3B 的效果与两倍于其规模的 Transformer 相当。性能高、效果好，Mamba 成为新的研究热点

现有架构问题

​ 序列建模的核心问题是：同时解决有效和高效。有效是指能够选择性记忆历史信息，解决长距离依赖（Long-Range Dependencies，LRDs）问题；高效是指计算高效。

​ 传统的模型如循环神经网络（RNNs）、卷积神经网络（CNNs）和 Transformers 在处理长距离依赖方面有专门的变体，但它们在处理超过 10000 步的极长序列时仍然面临挑战。

Transformer 问题

​ Transformer 的一个主要优点是，无论它接收到多长的输入，它都使用序列中的所有 token 信息（无论序列有多长）来对输入数据进行处理。但是为了获得全局信息，注意力机制在长序列上非常耗费显存。注意力创建一个矩阵，将每个 token 与之前的每个 token 进行比较。矩阵中的权重由 token 对之间的相关性决定。在训练过程中，Attention 计算可以并行化，所以可以极大地加快训练速度。但是在推理过程中，当生成下一个 token 时，我们需要重新计算整个序列的注意力。

​ 长度为$L$ 的序列生成 token 大约需要 $L^2$ 的计算量，如果序列长度增加，计算量会平方级增长。因此，需要重新计算整个序列是 Transformer 体系结构的主要瓶颈

RNN 的问题

​ 在生成输出时，RNN 只需要考虑之前的隐藏状态和当前的输入。这样不会重新计算以前的隐藏状态，这正Transformer 不具备的。这种结构可以让 RNN 进行快速推理，并且理论上可以无限扩展上下文长度，因为每次推理只取一个隐藏状态和当前输入，内存占用非常稳定。

​ RNN 的每个隐藏状态都是之前所有隐藏状态的聚合。但是这里会有一个问题。随着时间的推移，RNN 会忘记更久的信息，因为它只考虑前一个状态。并且 RNN 的这种顺序性产生了另一个问题。训练不能并行进行，因为它需要按顺序完成每一步

​ 与 Transformer 相比，RNN 的问题完全相反！它的推理速度非常快，但不能并行化导致训练很慢

状态空间模型 SSM

什么是 SSM

​ ssm是用于描述这些状态表示的模型，并根据某些输入预测其下一个状态可能是什么。状态空间模型（State Space Models，SSM）由如下方程定义：

$$\ \ y(t),u(t)\in \mathbb{R} \\ \boldsymbol x'(t) = \boldsymbol A \boldsymbol x(t) + \boldsymbol B u(t) \\ y(t) = \boldsymbol C \boldsymbol x(t) + D u(t) \\$$

$u(t)$ 为一维输入信号（一个标量），$y(t)$ 为输入信号（一个标量），$\boldsymbol x(t) \in \mathbb{R}^N$ 为 $N$ 维潜在状态，$A \in \mathbb{R}^{N \times N}$ 为状态转移矩阵，$\boldsymbol B \in \mathbb{R}^{N \times 1}$ 为输入影响状态的矩阵，$D$ 为直接控制输入到输出的参数（很多时候取值直接为0）

SSM 架构

​ 下图是 SSM 的架构，主要包含两个部分：状态更新方程和输出方程。

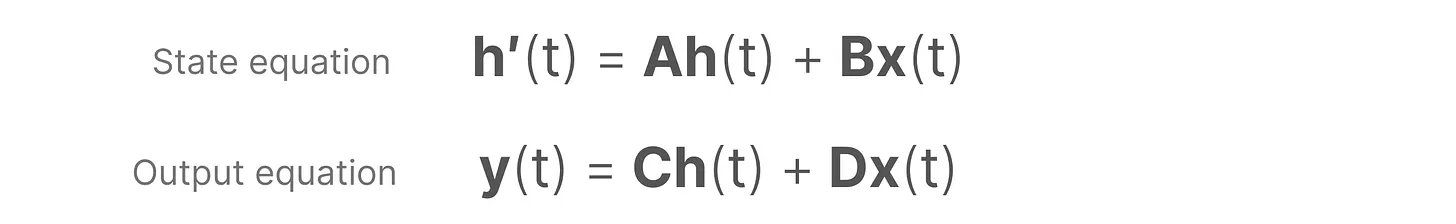
​ 第一行描述了状态方程，第二行描述了输出方程。这两个方程是SSM的核心

1. 上面的第一个方程是不和RNN循环结构：$\boldsymbol h_t = tanh(\boldsymbol (W h)_{t-1} +\boldsymbol U x_t)$非常类似：通过上一个隐藏状态和当前输入综合得到当前的隐藏状态，只是两个权重 $W$、$U$ 换成了 $A,B$ 两个系数，且去掉了非线性的激活函数 $tanh$
2. 但是转移方程为什么是导数？我觉得可能是想用导数去逼近下一时间状态：

$$\boldsymbol h(t+\Delta) \sim h(t) + \Delta \times \boldsymbol h'(t) \\ =\boldsymbol h(t) + \Delta \times \left( \boldsymbol {A h}(t) +\boldsymbol B x(t) \right) \\ = \boldsymbol h(t) + \Delta \boldsymbol {A h}(t) +\Delta \boldsymbol B x(t) \\ \overset{def} = \boldsymbol{\bar{A} h}(t) + \boldsymbol{\bar{B}}x(t)$$

建立对SSM中两个核心方程的统一视角

最终，我们可以通过下图统一这两个方程

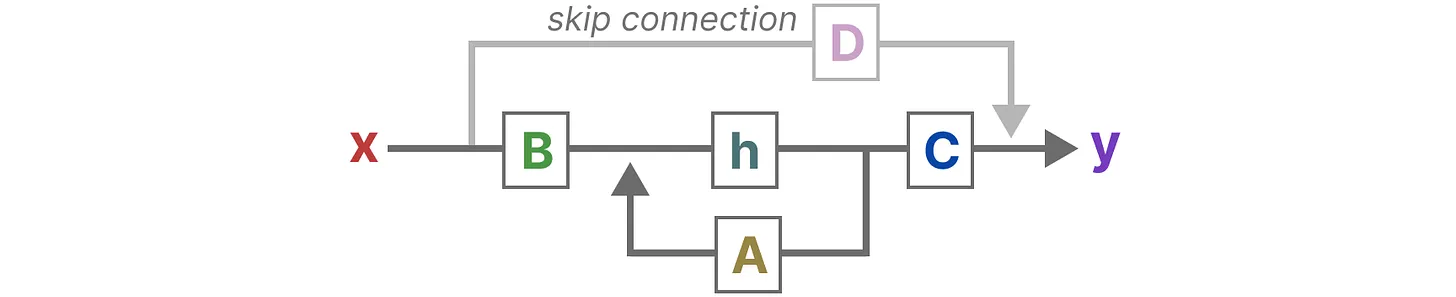
​ 看这个图我莫名地熟悉，这不就是信号流图吗？（盲猜以后有新的控制图对应的架构）

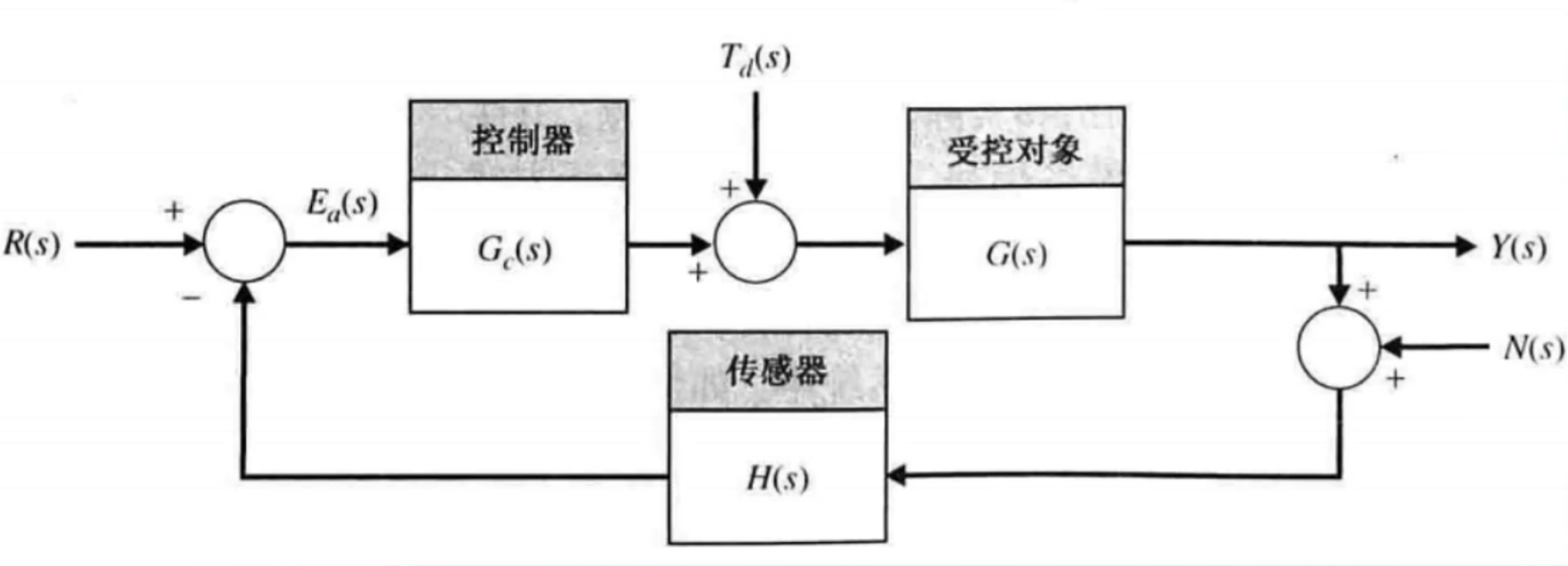
从SSM到S4的升级之路

​ SSM到S4的三步升级：离散化SSM、循环/卷积表示、基于HiPPO处理长序列

离散数据的连续化：基于零阶保持技术做连续化并采样

​ 由于除了连续的输入之外，还会通常碰到离散的输入(如文本序列)，不过，就算SSM在离散数据上训练，它仍能学习到底层蕴含的连续信息，因为在SSM眼里，sequence不过是连续信号signal的采样，或者说连续的信号模型是离散的序列模型的概括

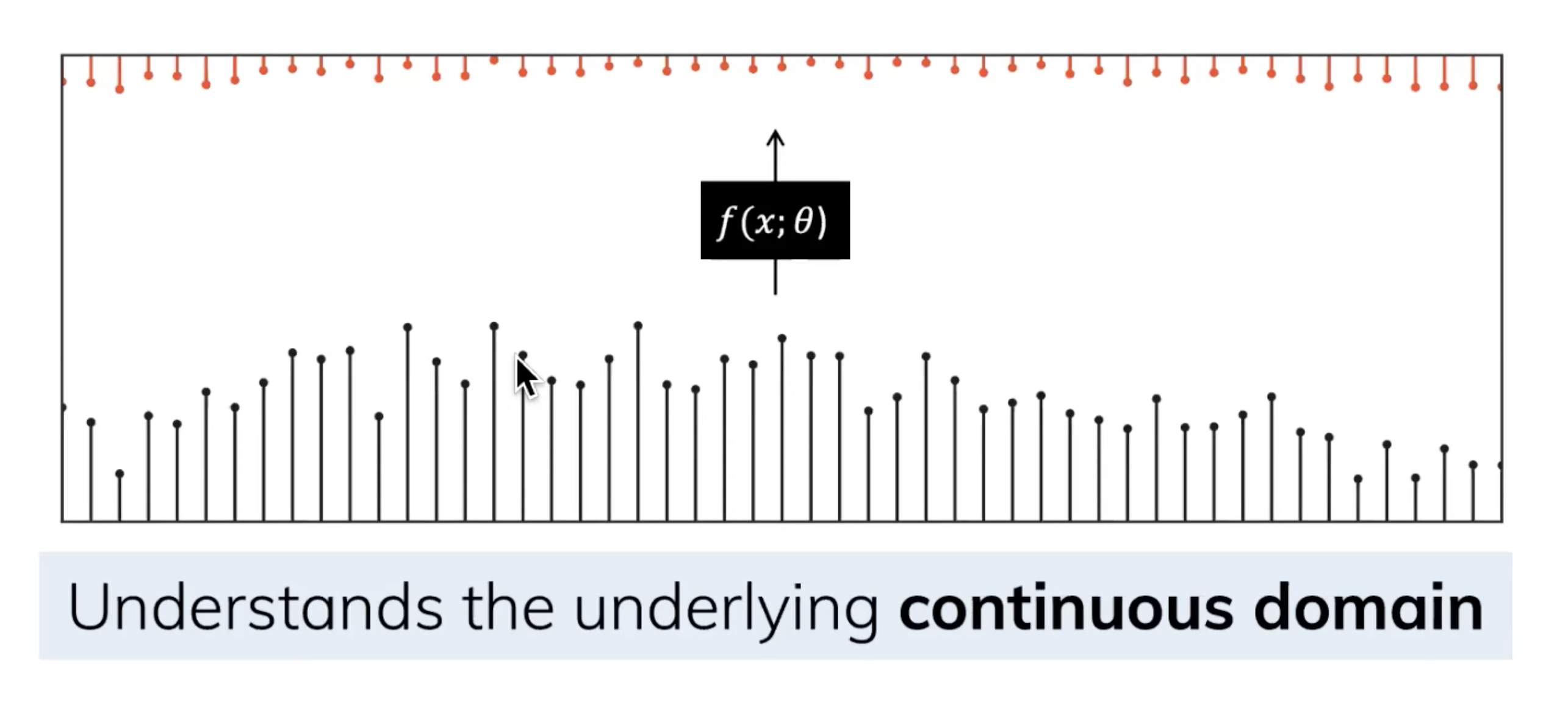
​ 那模型如何处理离散化数据呢？答案是利用零阶保持技术(Zero-order hold technique)

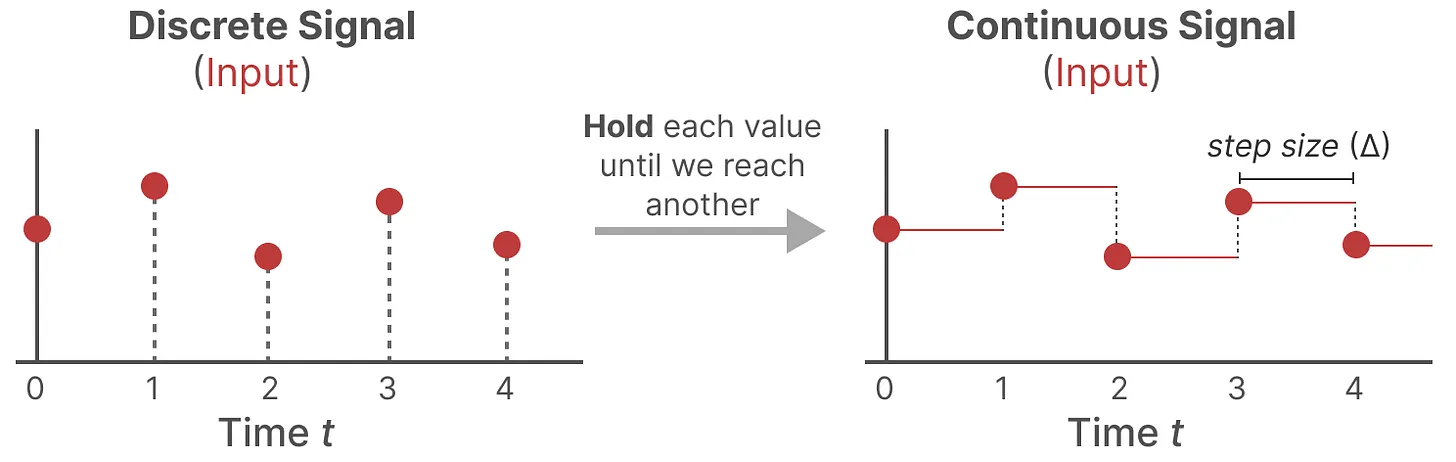
1. 首先，每次收到离散信号时，我们都会保留其值，直到收到新的离散信号，如此操作导致的结果就是创建了 SSM 可以使用的连续信号
2. 保持该值的时间由一个新的可学习参数表示，称为步长(siz) $\Delta$，它代表输入的阶段性保持(resolution)
3. 有了连续的输入信号后，便可以生成连续的输出，并且仅根据输入的时间步长对值进行采样（就是用零阶多项式插值）

$$\boldsymbol h(t+\Delta) \sim h(t) + \Delta \cdot \boldsymbol h'(t) \\ =\boldsymbol h(t) + \Delta \cdot \left( \boldsymbol {A h}(t) +\boldsymbol B x(t) \right) \\ = \boldsymbol h(t) + \Delta \cdot \boldsymbol {A h}(t) +\boldsymbol{\Delta \cdot B x}(t) \\ \overset{def} = \boldsymbol{\bar{A} h}(t) + \boldsymbol{\bar{B}}x(t)$$

零阶保持就是指用如下式子去逼近（注意 $\boldsymbol \Delta$ 是一个矩阵而不是差分算子）：

$$\boldsymbol{\bar{A}} = exp(\boldsymbol {\Delta A}) \\ \boldsymbol{\bar{B}} = (\boldsymbol{\Delta A})^{-1}(exp( \boldsymbol {\Delta A })- \boldsymbol I) \boldsymbol {\Delta B}$$

理解这两个式子：

• 上面 $\boldsymbol{\bar{A}=I+\Delta A}$ 的定义中，可以发现它与 $exp(\boldsymbol {\Delta A})$ 的泰勒展开是一样的
• 把 $exp(\boldsymbol{\Delta A-I})$ 部分代为 $\boldsymbol A$，那么这个式子就是恒等式

那么状态转移方程就可以改写为：

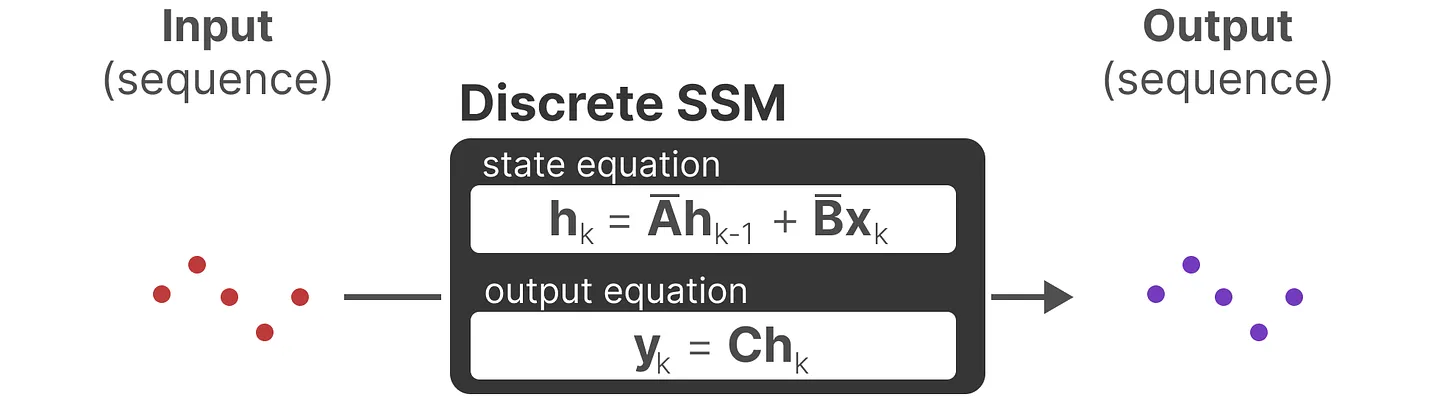
​ 注意：我们在保存时，仍然保存矩阵 $\boldsymbol A$ 的连续形式(而非离散化版本)，只是在训练过程中，连续表示被离散化(During training, the continuous representation is discretized)

循环结构表示：方便快速推理

​ 因此离散 SSM 允许可以用离散时间步长重新表述问题：

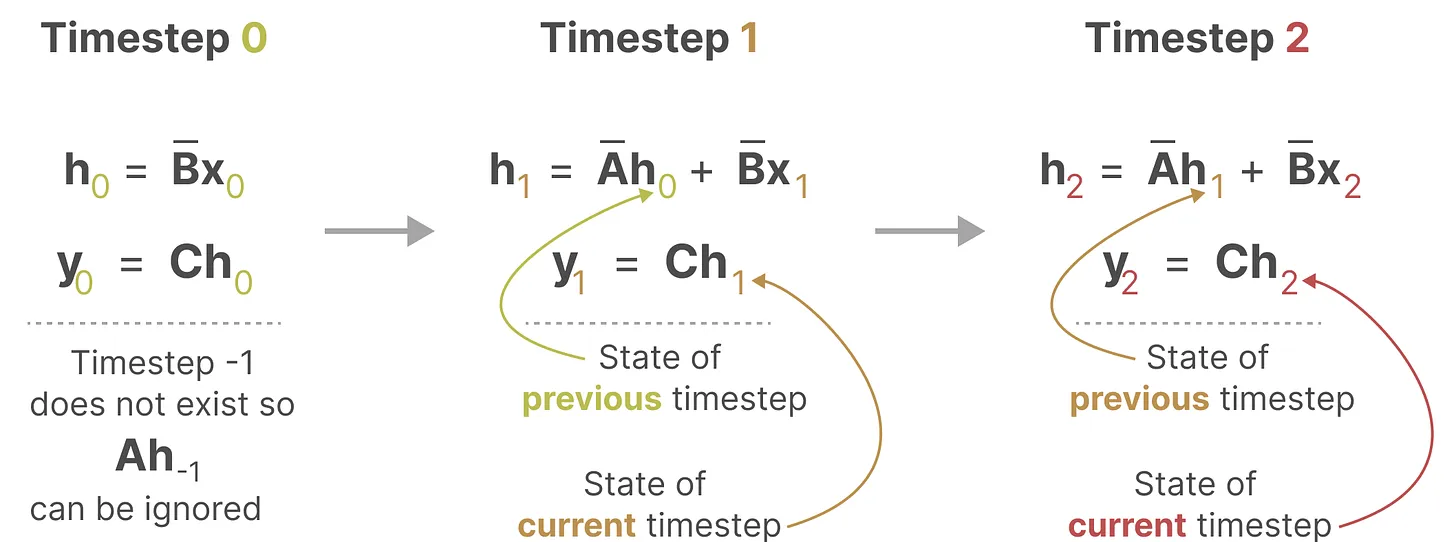
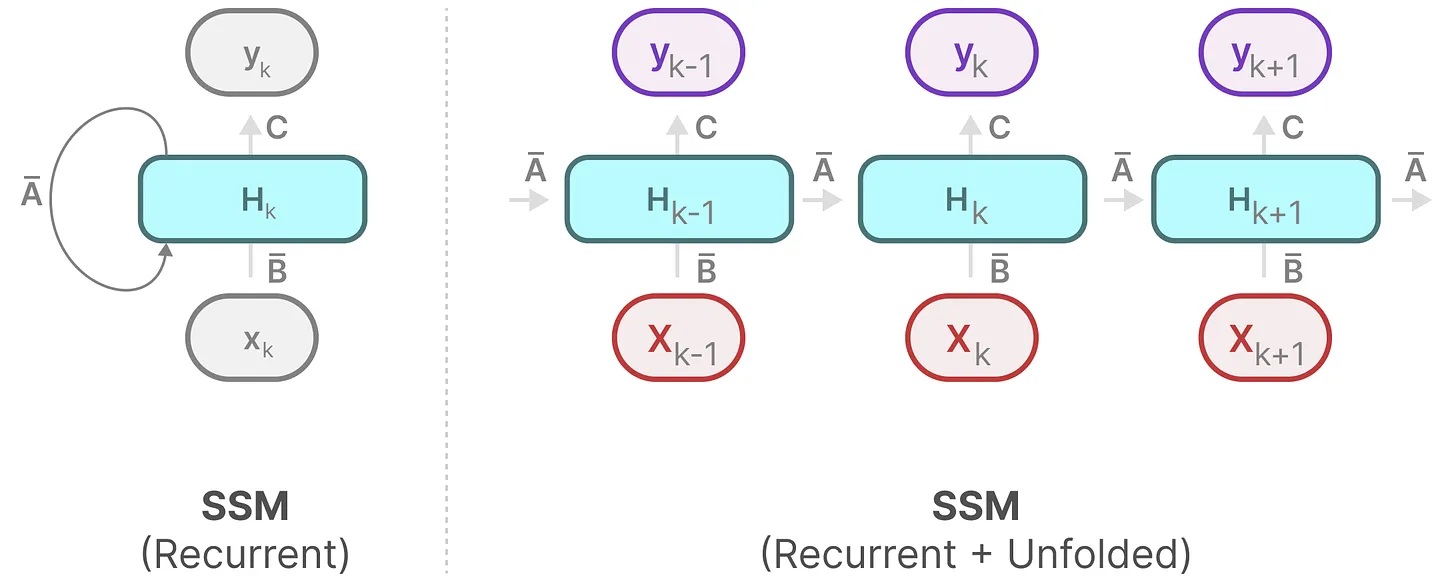
在每个时间步，都会涉及到隐藏状态的更新（其实就是RNN）：

$$y_2 = \boldsymbol {Ch}_2 = \boldsymbol {C(\bar{A}h_1+\bar{B})} x_2 \\ = \boldsymbol {C(\bar{A}}(\boldsymbol {\bar{A}h_0+\bar{B})}x_1+\boldsymbol {\bar{B}}) x_2 \\ = \boldsymbol {C\bar{A}^2\bar{B}}x_0 + \boldsymbol{C\bar{A}\bar{B}}x_1 + \boldsymbol {C\bar{B}}x_2$$

​ 因此mamba可以像RNN一样快速推理：

卷积结构表示：方便并行训练

​ 因为mamba没有采用非线性函数，它的状态转移都是线性的，因此可以使用卷积卷积视角，我们使用一维卷积视角：

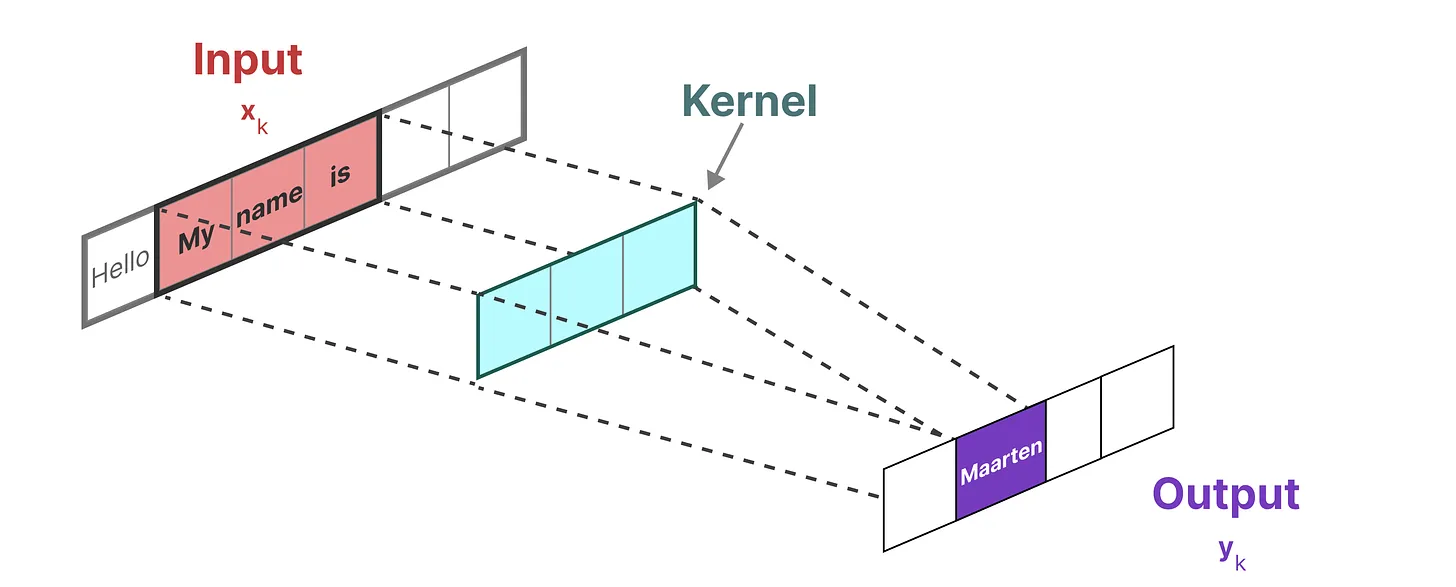
​ 而用来表示这个“卷积核”的内核源自 SSM 公式

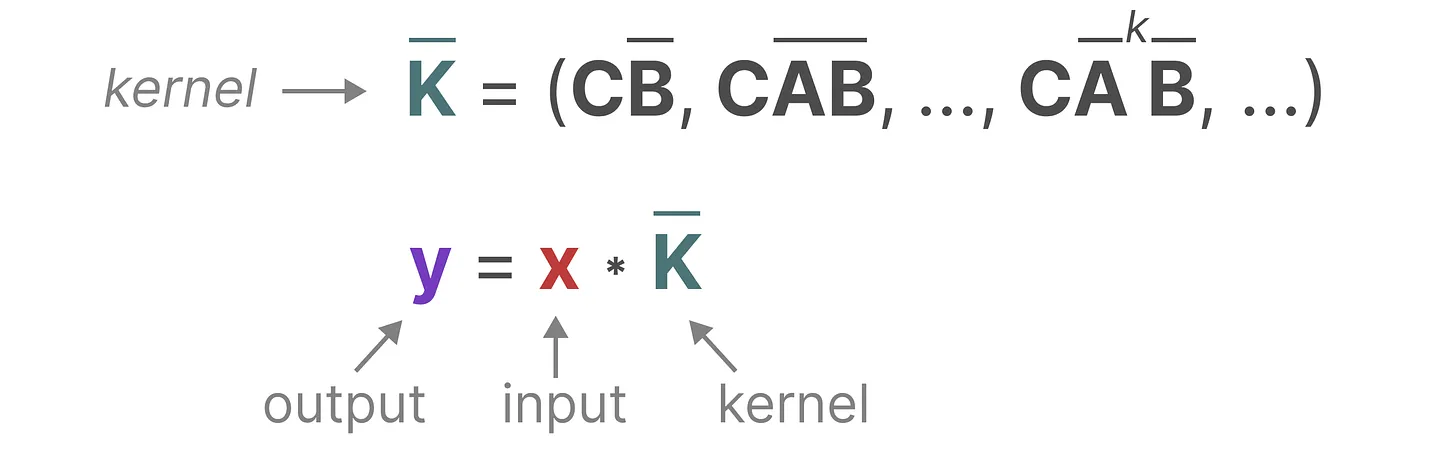
​ 将 SSM 表示为卷积的一个主要好处是它可以像卷积神经网络CNN一样进行并行训练。然而，由于内核大小固定，它们的推理不如 RNN 那样快速

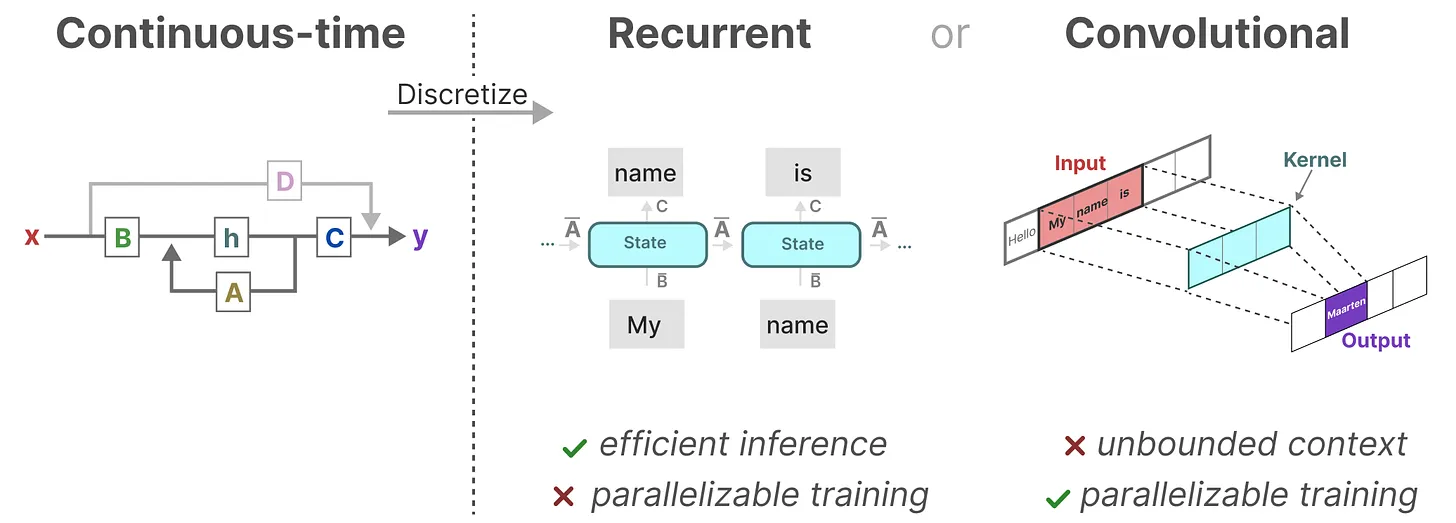
那有没两全其美的办法呢？最终是有的

1. 作为从输入信号到输出信号的参数化映射，SSMs可以当做是RNN与CNN的结合「These models can be interpreted as acombination of recurrent neural networks (RNNs) and convolutional neural networks (CNNs)」，即推理用RNN结构，训练用CNN结构

   

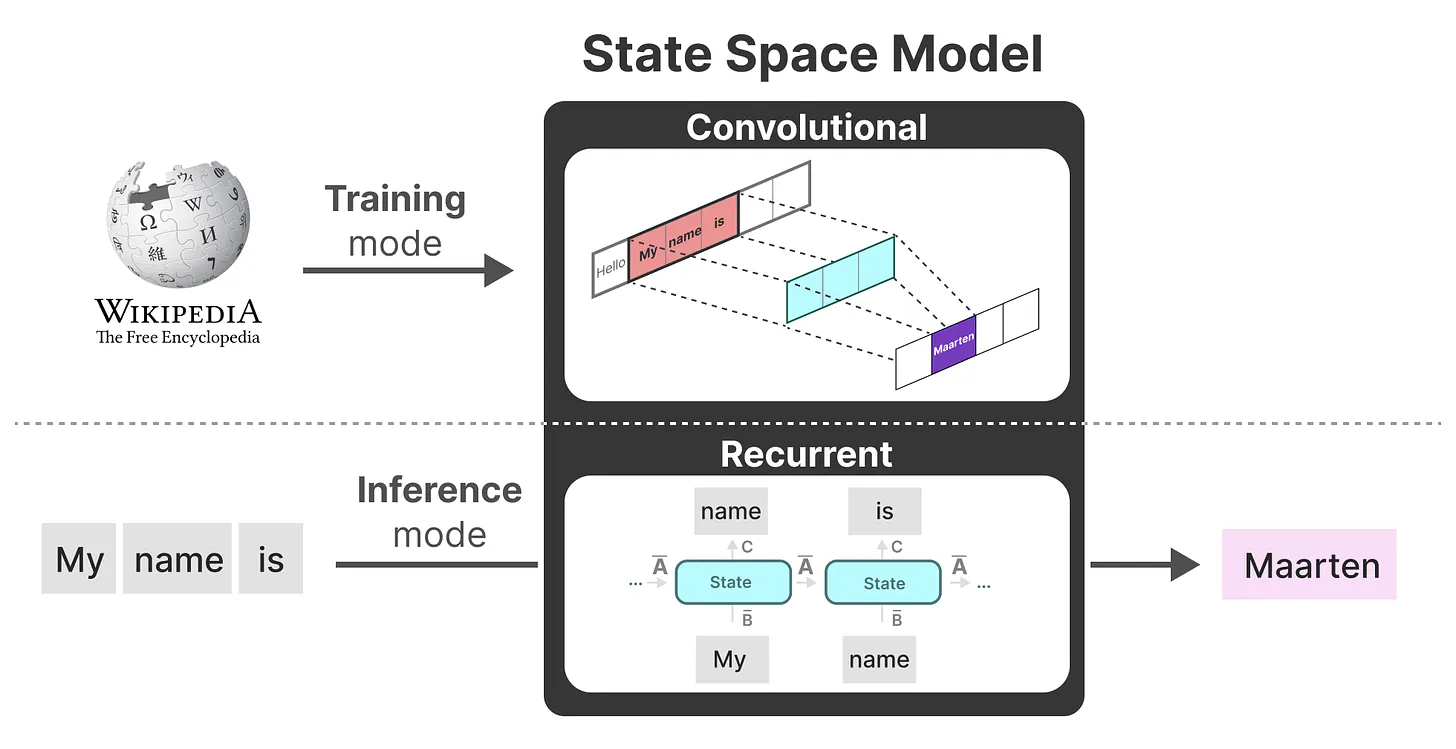
2. 总之，这类模型可以非常高效地计算为递归或卷积，在序列长度上具有线性或近线性缩放(This class of models can be computed very efficiently as either arecurrence or convolution, with linear or near-linear scaling in sequence length)

长距离依赖问题的解决之道——HiPPO

​ 如我们之前在循环表示中看到的那样，矩阵 $A$ 捕获先前previous状态的信息来构建新状态，同RNN一样，矩阵A只记住之前的几个token和捕获迄今为止看到的每个token之间的区别

那么我们怎样才能以保留比较长的memory的方式创建矩阵A呢？

1. 答案是可以使用Hippo(Hippo的全称是High-order Polynomial Projection Operator，其对应的论文为：HiPPO: Recurrent Memory with Optimal Polynomial Projections)（Mamba作者博士毕业论文，长达330页），解决如何在有限的存储空间中有效地解决序列建模的长距离依赖问题
2. HiPPO尝试将当前看到的所有输入信号压缩为系数向量(HiPPO attempts to compress all input signals it has seen thus far into a vector of coefficients)

它使用矩阵 $A$ 构建一个“可以很好地捕获最近的token并衰减旧的token”状态表示(to build a state representation that captures recent tokens well and decays older tokens)，说白了， 通过函数逼近产生状态矩阵 A 的最优解，其公式可以表示如下

$$A_{nk}\left\{ \begin{array}{c} \left( 2n+1 \right) ^{1/2}\left( 2k+1 \right) ^{1/2}\ \ \left( n>k \right)\\ n+1\ \ \ \ \ \left( n=k \right)\\ 0\ \ \ \left( n<k \right)\\ \end{array} \right.$$

​ 正由于HiPPO 矩阵可以产生一个隐藏状态来记住其历史(从数学上讲，它是通过跟踪Legendre polynomial的系数来实现的（勒让德多项式牛逼），这使得它能够逼近所有以前的历史)，使得在被应用于循环表示和卷积表示中时，可以处理远程依赖性

• 相比于随机初始化一个矩阵 $A$，使用Hippo初始化可以显著缓解遗忘问题
• 为了避免Hippo矩阵本身 $N^2$ 的尺寸带来过大的运算量，利用矩阵分解，可以使用低秩矩阵表示Hippo：

$$\boldsymbol {A = V \Lambda V^* - PQ^T = V(\Lambda - (V^*P)(V^*Q)^*)V^*}$$

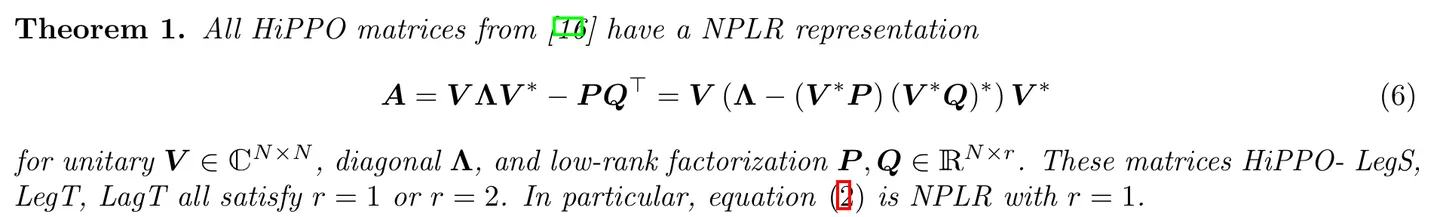
从s4到s6

参数化矩阵：

​ 对于矩阵 $\boldsymbol{\bar{A} ,\bar{B}}$，如果他们与输入无关，他们训练完之后就会平等的对待序列中每一个元素（看那个状态方程），我们想要动态调整模型对输入的“注意力”的话，就必须让矩阵 $\boldsymbol{\bar{A} ,\bar{B}}$ 与输入有关，即参数化矩阵，于是引出了我们的 s6 算法：

​

​ 我们的目的是参数化 $\boldsymbol{\bar{A},\bar{B}, \Delta}$ 矩阵（不参数化 $A$，好不容易初始化的不要随便破坏）

​ 假设输入数据 $x$ 的大小为 $(B, L, D)$，其中 $B, L, D$ 分别为 batch size，length，embedding dimension。再记 $N$ 为隐状态的维数，则矩阵 $\boldsymbol{\bar{A}, \bar{B}}$ 大小可以表示为:

$$shape(\boldsymbol {\bar {A}}) = shape(\boldsymbol {\bar {B}}) = (B, L, D, N)$$

• 但是这些矩阵太大了，如果直接从输入通过线性层再 reshape 的话会引入很大的参数量
• 其次，在之前的推导中我们知道 $\boldsymbol {\bar A， \bar{B}}$ 与 $\boldsymbol{\bar A, B, \Delta}$ 之间的关系，因此我们只需要将 $\boldsymbol {\Delta}$ 参数化即可
• 然后我们顺便也把输出方程的 $\boldsymbol C$ 也参数化

参数化代码如下：

$$\boldsymbol{\bar{A}} = exp(\boldsymbol {\Delta A}) \\ \boldsymbol{\bar{B}} = (\boldsymbol{\Delta A})^{-1}(exp( \boldsymbol {\Delta A })- \boldsymbol I) \boldsymbol {\Delta B}$$

delta = self.x2Delta(x)	# 通过一个线性层
delta = F.softplus(self.dt_proj(delta))
B = self.x2B(x)			# 通过一个线性层

A_bar = torch.exp(einops.einsum(delta, A, 'b l d_in, d_in n -> b l d_in n'))
B_bar = einops.einsum(delta, B, x, 'b l d_in, b l n, b l d_in -> b l d_in n')

硬件感知算法：

​ 既然我们将矩阵 $\boldsymbol{\bar{A} ,\bar{B}}$ 变得和输入有关，那么说明每一个时间点的 $\boldsymbol{\bar{A} ,\bar{B}}$ 都不一样了，那么我们就不能使用之前的卷积算法了！，即使如此，作者还是提出了一个算法能够让他并行计算：

选择性扫描算法：

• 放弃了使用卷积来描述 SSM，而是定义了一种新的“加”运算，在并行计算中，"连加"操作是可行的
• 假设运算操作的顺序而关联矩阵 $A$ 无关，我们会发现 $x_t$ 乘的矩阵都说源于 $x_t$ 的

定义新的运算过程：

我们的两个方程为：

$$\boldsymbol{h_t = \bar{A} h_{k-1} + \bar{B}x_k} \\ \boldsymbol{y_k = Ch_k} \\ \boldsymbol y_2 = \boldsymbol {C\bar{A1}\bar{A}_2\bar{B}_0}x_0 + \boldsymbol{C\bar{A}_2\bar{B}_1}x_1 + \boldsymbol {C\bar{B}_2}x_2$$

受此启发，我们定义运算：

$$(A_t, B_t x_t) \oplus (A_{t+1}, B_{t+1}x_{t+1}) = (A_tA_{t+1}, A_{t+1}B_tx_t + B_{t+1}x_{t+1})$$

​ 可以发现这个运算满足交换律和结合律，去该运算的第二项结果，虽然不是卷积运算，但是是一种并行运算

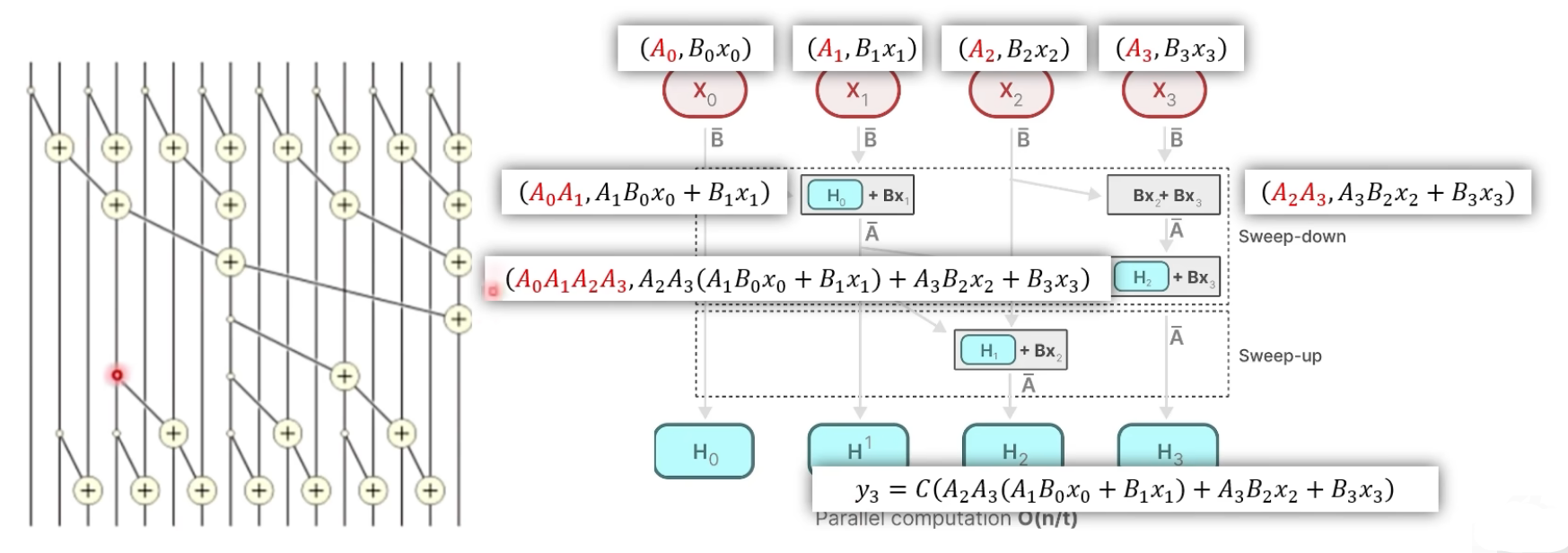
• 在上图的例子中，$x_3$ 对应的输出计算方式为：先分别对 $x_1,x_2$ 和 $x_3, x_4$ 进行上面的二元计算，再对这两个计算结果再进行一次二元计算即可

利用Mamba模型小的优势进一步加速

​ 由于Mamba模型的参数量较小，因此整个模型可以一次性全部再入到 GPU 的 SRAM 里面，把计算全部放在 SRAM 里面完成，这样就减少了大模型在 GPU 内反复把数据在 DRAM 和 SRAM 之间交换产生的时间耗费

​ 这一部分不精读，对 GPU 硬件知识要求比较高，我懒得看

Mamba最终架构：