常用Neck网络-1

SPP(Spatial Pyramid Pooling)

Motivation：

SPP的提出就是为了解决CNN输入图像大小必须固定的问题，从而可以使得输入图像高宽比和大小任意

网络结构解析：

SPP-Neck网络结构如下：

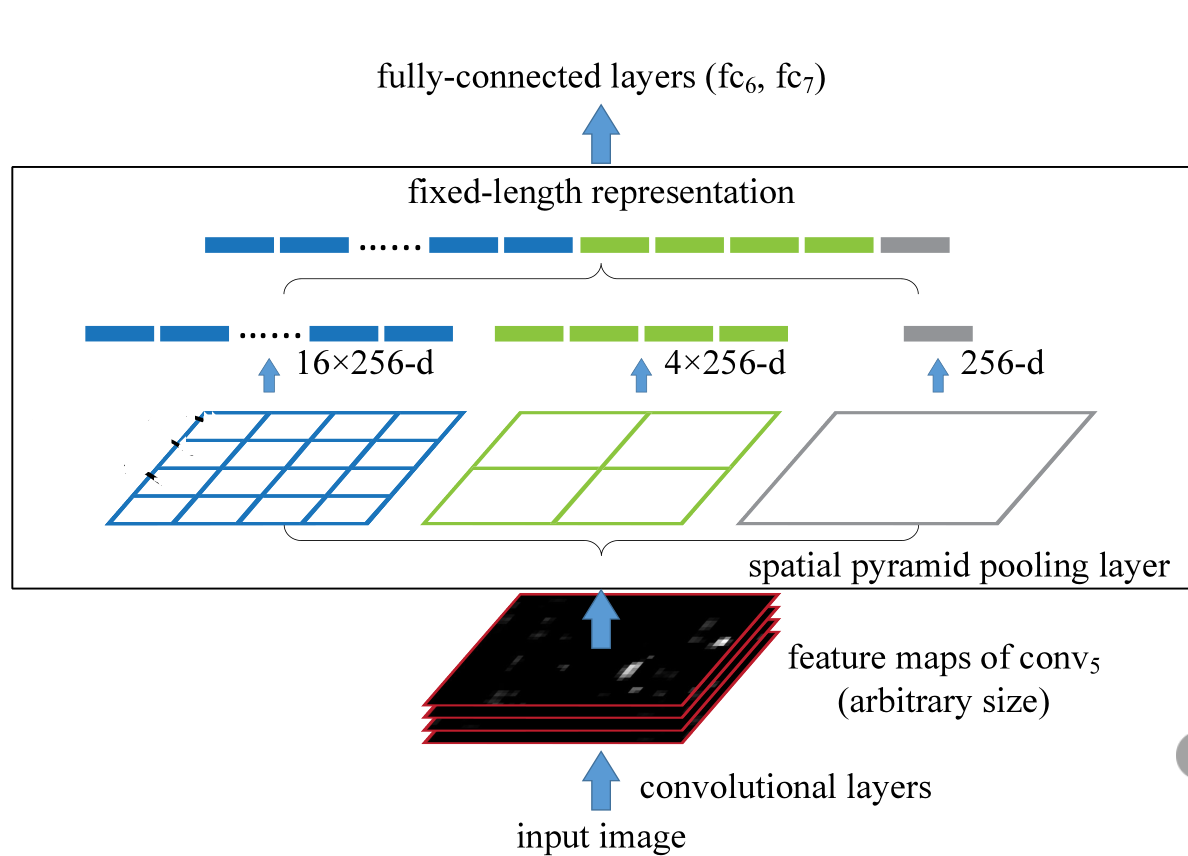
SPP-Neck

首先是输入层(input image),其大小可以是任意的
中间的部分就是SPP-Neck层，SPP会在最后一层卷积层输出的特征图上进行操作，将其划分为多个不同大小的子区域，并对每个子区域分别执行池化操作
- 最左边有是原特征图拆分成16份的图，256表示的是原特征图的channel对应在Linear层的维度，共有16个这样的Linear层(最常见的是使用等比分割以形成规则的网格，并不一定是等比分)
- 中间部分和右侧部分的网络同理，就是将原特征图分成了 $2 \times 2$ 和 $1 \times 1$ ，同理左边的部分

代码实现：

import math
import torch
import torch.nn as nn
import torch.nn.functional as F

# 构建SPP层(空间金字塔池化层)
class SPPLayer(nn.Module):

    def __init__(self, num_levels, pool_type='max_pool'):
        super().__init__()

        self.num_levels = num_levels
        self.pool_type = pool_type

    def forward(self, x):
        num, c, h, w = x.size()
        for i in range(self.num_levels):
            level = i+1
            kernel_size = (math.ceil(h / level), math.ceil(w / level))
            stride = (math.ceil(h / level), math.ceil(w / level))
            pooling = (math.floor((kernel_size[0]*level-h+1)/2), math.floor((kernel_size[1]*level-w+1)/2))

            # 选择池化方式 
            if self.pool_type == 'max_pool':
                tensor = F.max_pool2d(x, kernel_size=kernel_size, stride=stride, padding=pooling).view(num, -1)
            else if self.pool_type == 'avg_pool':
                tensor = F.avg_pool2d(x, kernel_size=kernel_size, stride=stride, padding=pooling).view(num, -1)

            # 展开、拼接
            if (i == 0):
                x_flatten = tensor.view(num, -1)
            else:
                x_flatten = torch.cat((x_flatten, tensor.view(num, -1)), 1)
        return x_flatten

ASPP(Atrous Spatial Pyramid Pooling)

Motivation:

可以认为是SPP在语义分割中的应用，结合了空洞卷积可在不丢失分辨率（不进行下采样）的情况下扩大卷积核的感受野。Deep CNN 中普通卷积对于其他任务还有一些致命性的缺陷。主要问题有：

内部数据结构丢失；空间层级化信息丢失
小物体信息无法重建 (假设有四个pooling layer 则任何小于 $2^4=16$ pixel 的物体信息将理论上无法重建

在这样问题的存在下，语义分割问题一直处在瓶颈期无法再明显提高精度，而 dilated convolution 的设计就良好的避免了这些问题

网络结构解析：

ASPP网络结构如下：

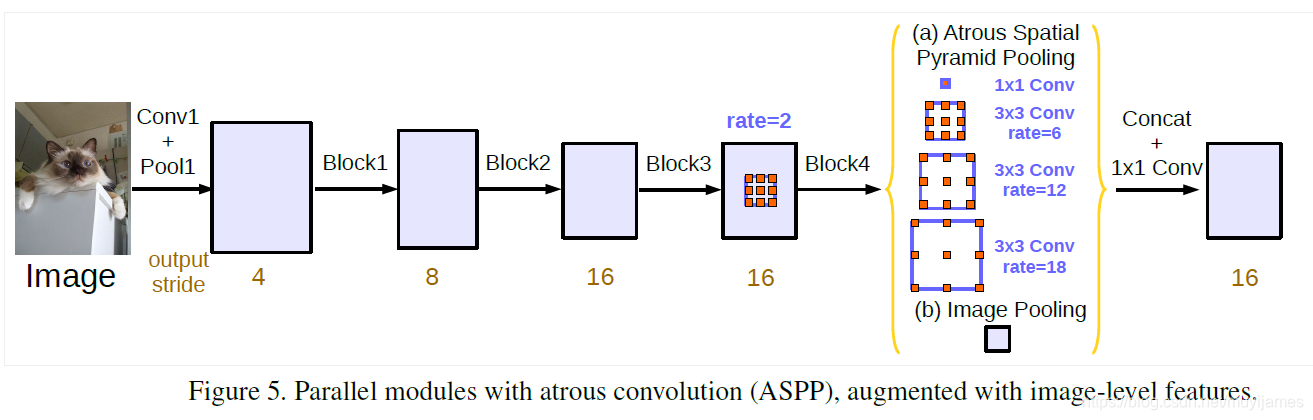
ASPP-network

中间黄色括号部分即为 ASPP-Neck，展开结构如下所示：

ASPP

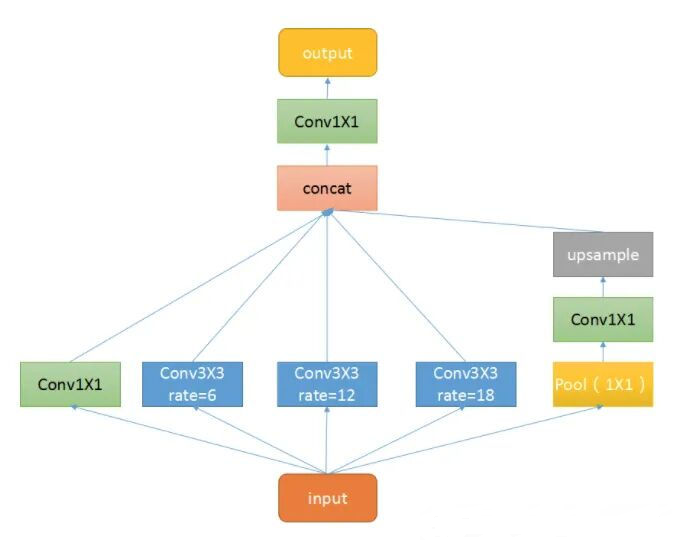
对于 input，网络会对 feature map 分别进行 $1 \times1 $ 和不同比例空洞卷积，这些操作都不改变 feature map 的大小
右边部分称为 ASPP Pooling，目的是为了得到语义信息，首先是一个 AdaptiveAvgPool2d 层。自适应均值池化就是不需要指定 kernel size 和 stride，只需指定最后的输出尺寸，再进行 $1 \times 1$ 卷积后上采样
最终将这些 feature map concat 到一起再特征融合即可

代码实现：

# 空洞卷积
class ASPPConv(nn.Sequential):
    def __init__(self, in_channels, out_channels, dilation):
        modules = [
            nn.Conv2d(in_channels, out_channels, 3, padding=dilation, dilation=dilation, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU()
        ]
        super(ASPPConv, self).__init__(*modules)

# 池化 -> 1*1 卷积 -> 上采样
class ASPPPooling(nn.Sequential):
    def __init__(self, in_channels, out_channels):
        super(ASPPPooling, self).__init__(
            nn.AdaptiveAvgPool2d(1),  # 自适应均值池化
            nn.Conv2d(in_channels, out_channels, 1, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU())

    def forward(self, x):
        size = x.shape[-2:]
        for mod in self:
            x = mod(x)
        # 上采样
        return F.interpolate(x, size=size, mode='bilinear', align_corners=False)  

# 整个 ASPP 架构
class ASPP(nn.Module):
    def __init__(self, in_channels, atrous_rates, out_channels=256):
        super(ASPP, self).__init__()
        modules = []
        # 1*1 卷积
        modules.append(nn.Sequential(
            nn.Conv2d(in_channels, out_channels, 1, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU()))

        # 多尺度空洞卷积
        rates = tuple(atrous_rates)
        for rate in rates:
            modules.append(ASPPConv(in_channels, out_channels, rate))

        # 池化
        modules.append(ASPPPooling(in_channels, out_channels))

        self.convs = nn.ModuleList(modules)
        
        # 拼接后的卷积
        self.project = nn.Sequential(
            nn.Conv2d(len(self.convs) * out_channels, out_channels, 1, bias=False),
            nn.BatchNorm2d(out_channels),
            nn.ReLU(),
            nn.Dropout(0.5))

    def forward(self, x):
        res = []
        for conv in self.convs:
            res.append(conv(x))
        res = torch.cat(res, dim=1)
        return self.project(res)

NAS-FPN(Neural Architecture Search)

Motivation:

采用神经网络结构搜索（Neural Architecture Search, NAS），在一个覆盖所有跨尺度连接的新型可扩展搜索空间中发现了一个新的特征金字塔结构，NAS-FPN。与原始FPN相比，NAS-FPN显著提高了目标检测的性能，并取得了更好了速度-精度的 trade-off

网络结构解析：

作者提出了merging cell作为FPN的basic building block，将任何两层的输入特征融合为一层的输出特征：

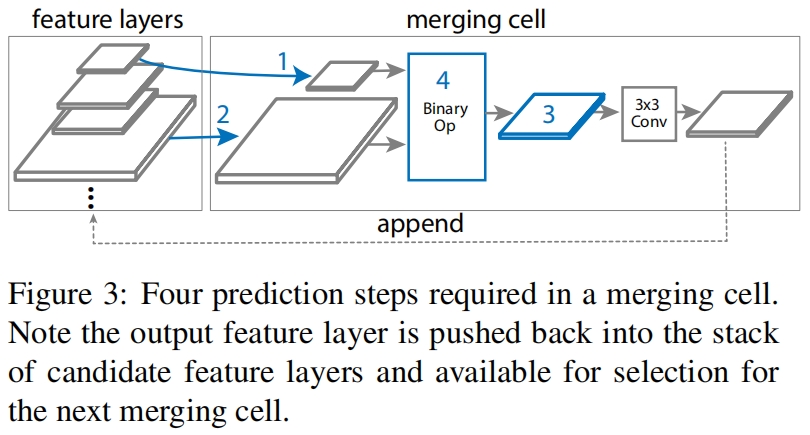
搜索示意图

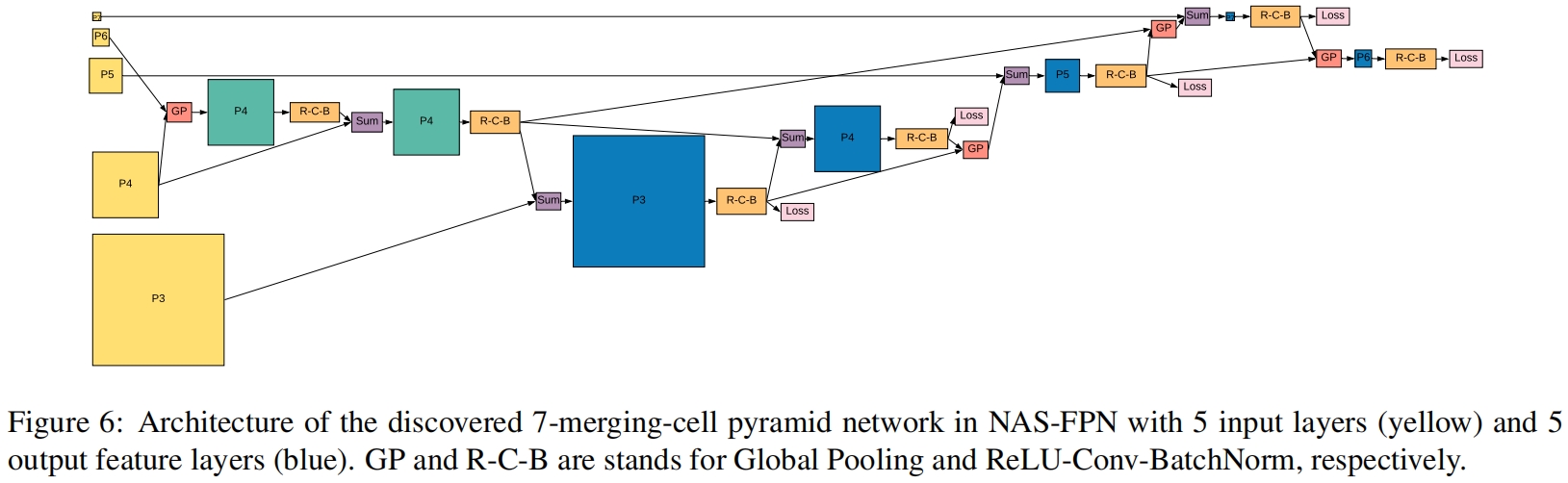
最终搜索到的NAS-FPN的完整结构如图6所示

NAS-FPN

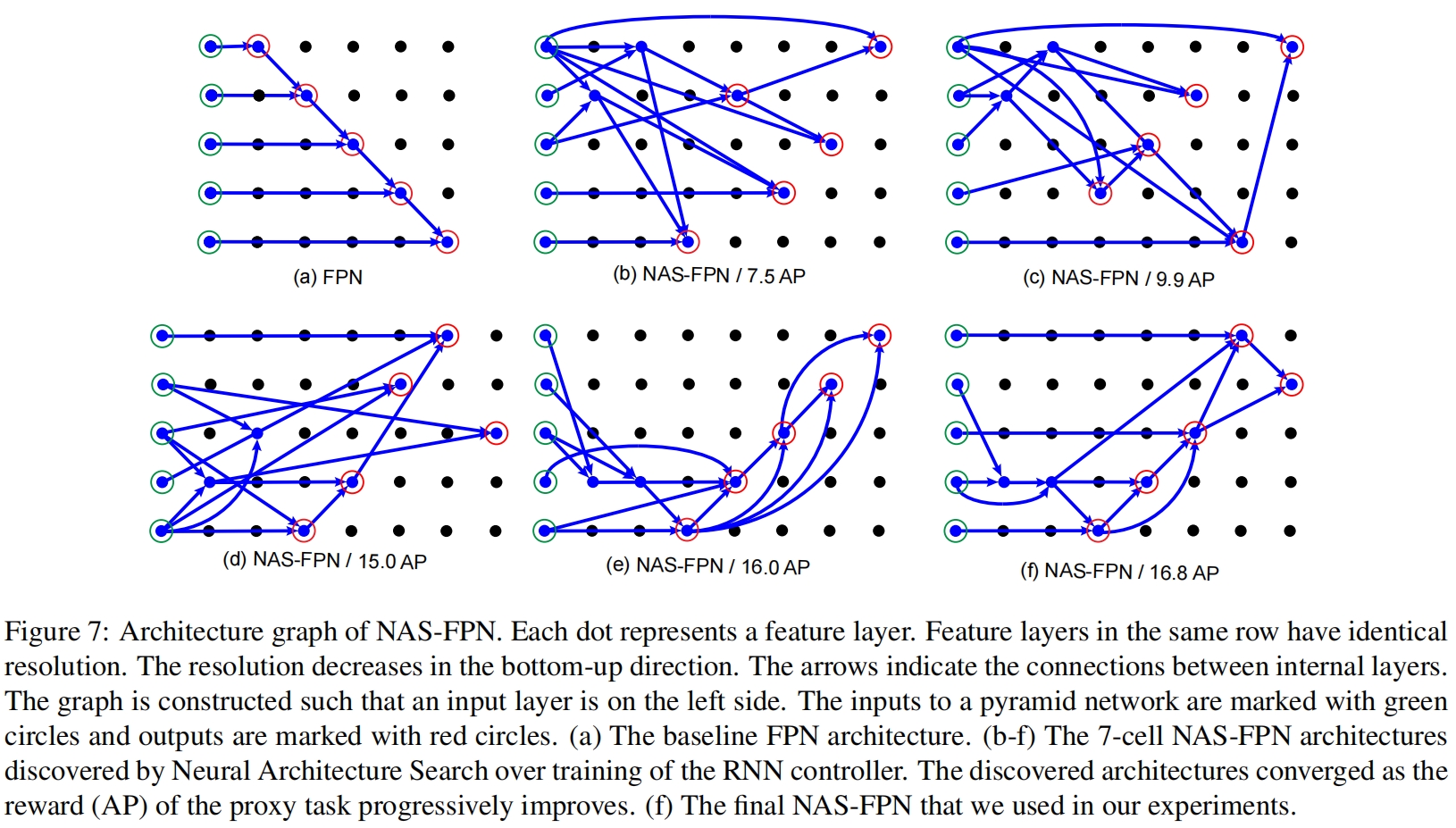
如下图所示，下图其中(a)是原始FPN结构，(b)-(f)的精度逐渐变高，(f)是最终的NAS-FPN结构，每个圆点代表一个特征层，绿色圆圈表示输入层，红色圆圈表示输出层，这些特征层在同一个行中具有相同的分辨率。箭头指示特征层之间的连接或信息流的方向

网格搜索示意

代码实现：

以 mmdetection 中的一部分代码为例：

def forward(self, inputs: Tuple[Tensor]) -> tuple:
    # [(8,256,160,160),
    #  (8,512,80,80),
    #  (8,1024,40,40),
    #  (8,2048,20,20)]
    """Forward function.
     Args:
        inputs (tuple[Tensor]): Features from the upstream network, each
            is a 4D-tensor.
    Returns:
        tuple: Feature maps, each is a 4D-tensor.
    """
    # build P3-P5
    feats = [
        lateral_conv(inputs[i + self.start_level])
        for i, lateral_conv in enumerate(self.lateral_convs)
    ]  # [(8,256,80,80),(8,256,40,40),(8,256,20,20)]
    # build P6-P7 on top of P5
    for downsample in self.extra_downsamples:
        feats.append(downsample(feats[-1]))  # [..., (8,256,10,10),(8,256,5,5)]
 
    p3, p4, p5, p6, p7 = feats
 
    for stage in self.fpn_stages:
        # gp(p6, p4) -> p4_1
        # print(stage['gp_64_4'])
        p4_1 = stage['gp_64_4'](p6, p4, out_size=p4.shape[-2:])  # (8,256,40,40)
        # sum(p4_1, p4) -> p4_2
        p4_2 = stage['sum_44_4'](p4_1, p4, out_size=p4.shape[-2:])  # (8,256,40,40)
        # sum(p4_2, p3) -> p3_out
        p3 = stage['sum_43_3'](p4_2, p3, out_size=p3.shape[-2:])  # (8,256,80,80)
        # sum(p3_out, p4_2) -> p4_out
        p4 = stage['sum_34_4'](p3, p4_2, out_size=p4.shape[-2:])  # (8,256,40,40)
        # sum(p5, gp(p4_out, p3_out)) -> p5_out
        p5_tmp = stage['gp_43_5'](p4, p3, out_size=p5.shape[-2:])  # (8,256,20,20)
        p5 = stage['sum_55_5'](p5, p5_tmp, out_size=p5.shape[-2:])  # (8,256,20,20)
        # sum(p7, gp(p5_out, p4_2)) -> p7_out
        p7_tmp = stage['gp_54_7'](p5, p4_2, out_size=p7.shape[-2:])  # (8,256,5,5)
        p7 = stage['sum_77_7'](p7, p7_tmp, out_size=p7.shape[-2:])  # (8,256,5,5)
        # gp(p7_out, p5_out) -> p6_out
        p6 = stage['gp_75_6'](p7, p5, out_size=p6.shape[-2:])  # (8,256,10,10)
 
    return p3, p4, p5, p6, p7

PANet(Path Aggregation Network)

Motivation:

dense prediction task 不仅要关心语义信息，还要关注图像的精确到像素点的浅层信息。PANet 最大的贡献是提出了一个自顶向下和自底向上的双向融合骨干网络，同时在最底层和最高层之间添加了一条“short-cut”，用于缩短层之间的路径

网络结构解析：

PANet网络结构如下：
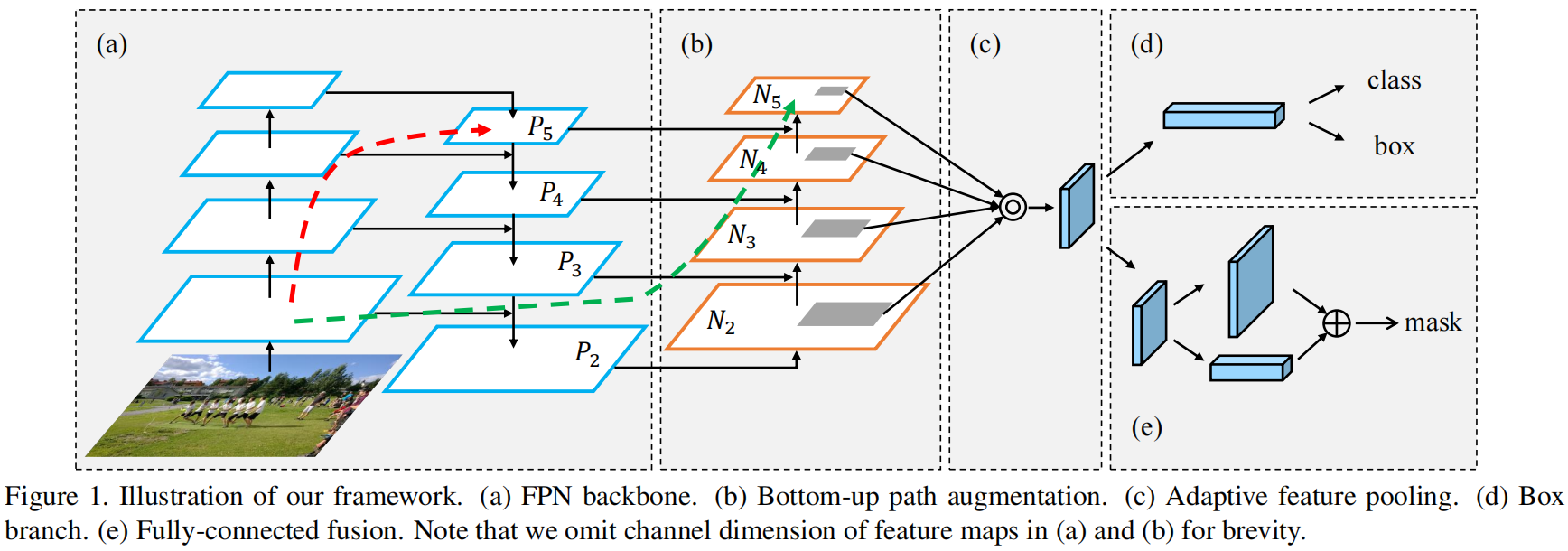
PANet

具体的实现比较简单，就是在FPN的基础上加上了一个Neck部分，再通过两条虚线将浅层网络信息跳连到深层网络中（按理来说PANet是可以在NAS-FPN那篇论文中搜索到的，查了一下确实PANet的发表时间早于NAS-FPN）

其它：

还有各种FPN网络如PANet、ASFF、NAS-FPN、BiFPN、Recursive-FPN…太多了，有需要的时候再查

个人感想：要是 NAS 能够改变算法能够搜索地足够快的话，能把这些 FPN 网络全部搜索完就好了，哪需要认为设计这么多乱七八糟的 FPN…

Wandb教程(3) 上一篇

FeatUp(1) 下一篇