intro

什么是强化学习

​ 强化学习是机器通过与环境交互来实现目标的一种计算方法。机器和环境的一轮交互是指，机器在环境的一个状态下做一个动作决策，把这个动作作用到环境当中，这个环境发生相应的改变并且将相应的奖励反馈和下一轮状态传回机器（因此强化学习示意图很像RNN网络）。这种交互是迭代进行的，机器的目标是最大化在多轮交互过程中获得的累积奖励的期望。强化学习用智能体（agent）概念来表示做决策的机器。相比于有监督学习中的“模型”，强化学习中的“智能体”强调机器 不但可以感知周围的环境信息，还可以通过做决策来直接改变这个环境，而不只是给出一些预测信号（预测型 AI 和决策型 AI）

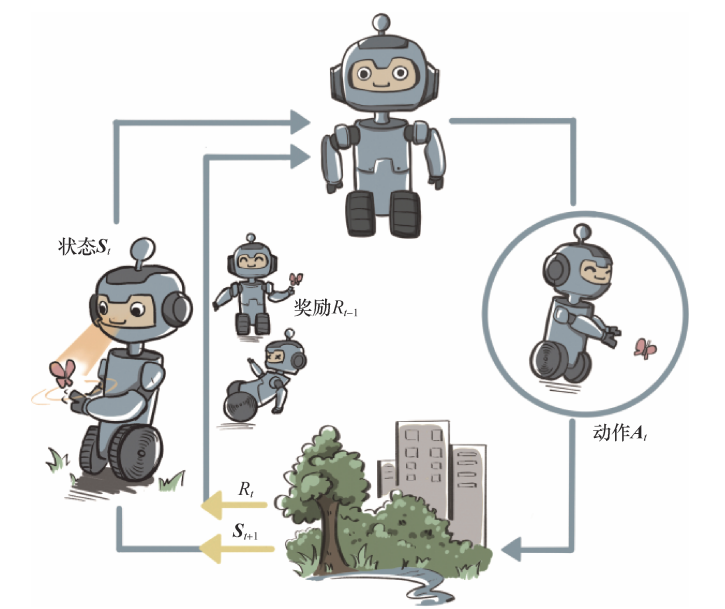
强化学习的环境

​ 环境这样一个自身演变的随机过程中加入一个外来的干扰因素，即智能体的动作， 那么环境的下一刻状态的概率分布将由当前状态和智能体的动作来共同决定，用最简单的数学公式（马尔可夫决策过程）表示则是：

$$\text{环境下一刻状态} \sim P( \cdot \mid \text{当前状态，智能体的动作})$$

每一轮状态转移都伴随着两方面 的随机性：一是智能体决策的动作的随机性，二是环境基于当前状态和智能体动作来采样下一刻状态的随机性

强化学习的数据：

​ 有监督学习的任务建立在从给定的数据分布中采样得到的训练数据集上，通过优化在训练 数据集中设定的目标函数（如最小化预测误差）来找到模型的最优参数。这里，训练数据集背 后的数据分布是完全不变的。 在强化学习中，数据是在智能体与环境交互的过程中得到的。如果智能体不采取某个决策动作，那么该动作对应的数据就永远无法被观测到，所以当前智能体的训练数据来自之前智能体的决策结果。因此，智能体的策略不同，与环境交互所产生的数据分布（占用度量）就不同

• 强化学习的策略在训练中会不断更新，其对应的数据分布（即占用度量）也会相应地 改变。因此，强化学习的一大难点就在于，智能体看到的数据分布是随着智能体的学习而不断 发生改变的
• 由于奖励建立在状态动作对之上，一个策略对应的价值其实就是一个占用度量下对应 的奖励的期望，因此寻找最优策略对应着寻找最优占用度量

与其它学习的区别

​ 对于一般的有监督学习任务，我们的目标是找到一个最优的模型函数，使其在训练数据集上最小化一个给定的损失函数。在训练数据独立同分布的假设下，这个优化目标表示最小化模型在整个数据分布上的泛化误差（generalization error），用简要的公式可以概括为：

$$\text{最优模型} = \arg\min_{\text{模型}} E_{\text{(特征，标签)}\text{数据分布}}[\text{损失函数(标签,模型)}]$$

相比之下，强化学习任务的最终优化目标是最大化智能体策略在和动态环境交互过程中的价值。根据1.5节的分析，策略的价值可以等价转换成奖励函数在策略的占用度量上的期望，即：

$$\text{最优策略} = \arg\max_{\text{策略}} E_{\text{(状态，动作) }\sim \text{策略的占用度量}}[\text{奖励函数(状态,动作)}]$$

（1）有监督学习和强化学习的优化目标相似，即都是在优化某个数据分布下的一个分数值的期望

（2）二者优化的途径是不同的，有监督学习直接通过优化模型对于数据特征的输出来优化目标，即修改目标函数而数据分布不变；强化学习则通过改变策略来调整智能体和环境交互数据的分布，进而优化目标，即修改数据分布而目标函数不变

按照如何找到最优策略分类

​ 在强化学习（Reinforcement Learning, RL）中，Value-Based RL、Policy-Based RL 和 Model-Based RL 是三种主要方法，它们在概念和实现上有显著区别。

Value-Based RL

​ Value-Based RL 通过学习价值函数（value function）评估状态或状态-动作对的预期累积奖励，不需要显式地学习环境的动态模型，利用近似动态规划（approximate dynamic programming）更新价值函数（model-free，直接从交互数据中学习，而不需要构建环境模型）

• 典型算法有价值迭代算法，直接学习价值函数而非对策略进行直接更新来隐式地改进策略，由此来学习最优的决策

• 算法特点：稳定，逐步收敛到最优解，适用于离散动作空间。但在高维或连续空间计算复杂，需函数近似（如神经网络）

Policy-Based RL

​ Policy-Based RL 直接学习策略（policy），通过优化策略最大化累积奖励（仍然是 model-free 算法）

• 典型算法就是策略迭代算法，通过不断进行策略改进来学习策略

• 算法特点优点：适用于连续动作空间，可学习随机策略。但是收敛性差，样本效率低。

Model-Based RL

​ Model-Based RL 学习环境模型（状态转移模型和奖励函数），通过模型进行内部规划和模拟优化策略（使用模型来预测未来的状态和奖励）

• 典型算法就是 dynamic programming，它依赖于完整的环境模型（状态转移概率和奖励函数）。主要有两种方法估计环境模型，策略迭代和价值迭代

• 算法特点：高效，减少与真实环境的交互。模型准确性关键，复杂环境学习准确模型困难。

---

​ 实际上 model-free RL 的本质仍然是 model-based 的，对值函数的估计本身就隐式包含了对环境的一种估计，但也不是全是 model-based，因为值函数还收策略的影响，因此可以认为 model-free RL 对环境的估计已经在值函数估计中做了

---

符号定义：

基础定义：

状态（State）与动作（Action）：

• 动作 和 动作全集 定义为：$a , \mathcal{A} \quad (a \in \mathcal{A})$
• 状态 和 状态全集 定义为：$s, \mathcal{S} \quad (s \in \mathcal{S})$

当状态和动作的表示为向量值时，则用粗体表示：$\boldsymbol{a, s}$，在 MDP 中，表示动作和状态的随机变量（向量）记为 $S_t,A_t$。

策略（Policy）$\pi$：

• 确定性策略：对于每一个状态 $s$，策略 $\pi$ 映射到一个特定的动作 $a$，即 $\pi : \mathcal{S} \to \mathcal{A}$
• 随机性策略：策略 $\pi$ 定义了一个概率分布，表示在状态 $s$ 下采取动作 $a$ 的概率，即 $\pi(a|s): \mathcal{S} \times \mathcal{A} \to [0,1]$

MDP 中的概念

奖励分布 $\mathcal{R}(\cdot |s,a)$：

​ 奖励分布记作 $\mathcal{R}(r | s, a)$，表示在状态 $s$ 下采取动作 $a$ 时获得奖励 $r$ 的概率：

$$\mathcal{R}(r | s, a) = P(R_t = r | S_{t-1} = s, A_{t-1} = a)$$

状态转移概率分布 $P(s' | s, a)$：

​ 状态转移概率分布记作 $P(s' | s, a)$，表示在状态 $s$ 下采取动作 $a$ 后转移到状态 $s'$ 的概率：

$$P(s'|s,a) = P(S_{t+1} = s' | S_t = s, A_t = a)$$

即时奖励 $R_t$：

​ 即时奖励 $R_t$ 是一个随机变量，表示在时间步 $t$ 获得的奖励。它是根据奖励分布 $\mathcal{R}(r | s, a)$ 采样得到的：

$$R_t \sim \mathcal{R}(\cdot | S_{t-1}, A_{t-1})$$

​ 在确定性环境中，奖励分布退化为一个确定性的函数，即时奖励 $R_t$ 就是奖励函数 $r(s, a)$ 的确定性输出：

$$R_t = r(S_{t-1}, A_{t-1})$$

奖励 $r(s,a)$：

​ 奖励 $r(s,a)$ 定义为 $R_t$ 的期望，表示在状态 $s$ 下采取动作 $a$ 时获得的平均奖励：

$$r(s,a) = \mathbb{E}_{s^\prime \sim P(\cdot|s,a)}[R_t | S_{t-1} = s, A_{t-1} = a]$$

​ 在随机性环境中，$r(s,a)$ 是奖励分布 $\mathcal{R}(r | s, a)$ 的期望值，而在确定性环境中，$r(s,a)$ 就是即时奖励 $R_t$ 的确定性值

累计折扣奖励 $G_t$：

​ 累计折扣奖励 $G_t$ 是基于策略 $\pi$ 和环境动态采样得到的一系列即时奖励 $R_t,R_{t+1},R_{t+2},\cdots$ 的加权和。具体采样过程如下：

• 从某个初始状态 $S_t=s$ 开始。根据策略 $\pi(a|s)$ 选择动作 $A_t=a$，根据状态转移概率 $P(s^\prime |s,a)$ 采样得到下一个状态 $S_{t+1}=s^\prime$。根据奖励分布 $R(r|s,a)$ 采样得到即时奖励 $R_{t+1}$，重复上面骤，得到 $R_{t+1}, R_{t+2},\dots$ 可以得到一列奖励序列

累计折扣奖励 $G_t$ 就是这个序列的加权和，公式表示为：

$$G_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \dots = \sum_{i=0}^\infty \gamma^i R_{t+i}$$

其中 $R_{t+i} \sim \mathcal{R}(\cdot|S_{t+i}, A_{t+i})$，$A_{t+i} \sim \pi(\cdot|S_{t+i})$

动作值函数：

​ 表示在给定策略 $\pi$ 下，从状态 $s$ 执行动作 $a$ 后，预期可以获得的累积折扣奖励，则 $Q^\pi(s,a)=Q: \mathcal{S} \times \mathcal{A} \to \mathbb{R}$，其中 $\Pi$ 为策略空间，即所有可能的策略集合。记 $Q^*(s,a)$ 为最优状态值函数。

​ $\pi$ 是动作值函数的一个输入，因此动作值函数是定义在函数空间和标量空间的笛卡尔积上的函数，因此可以视为一个广义的泛函。在实际中我们不怎么将 $\pi$ 写到 $Q$ 内部而是写在上标处

\begin{align} Q^\pi(s, a) =& \mathbb{E}_\pi[G_t | S_t = s, A_t = a] \\ =& \mathbb{E}_{\pi, s^\prime \sim P(\cdot| s,a)} [R_t + \gamma V^\pi(s^\prime)| S_t = s, A_t = a] \\ =& r(s,a) + \gamma \sum_{a^\prime}P(s^\prime|s,a)V^\pi(s^\prime) \end{align}

状态值函数：

​ 表示在给定策略 $\pi$ 下，从状态 $s$ 开始，预期可以获得的累积折扣奖励。$V^\pi(s)=V: \mathcal{S} \to \mathbb{R}$，记 $V^*(s)$ 为最优状态值函数。

则根据定义可以很简单的写出两个值函数之间的关系：

\begin{align} V^\pi(s) =& \mathbb{E}_\pi[G_t | S_t = s] \\ =&\mathbb{E}_{a \sim \pi(\cdot|s)} [Q^\pi(s,a)| S_t = s] \\ =& \sum_a \pi(a|s) Q^\pi(s,a) \end{align}

几个概念的区分

符号	公式	核心区别
$R_t$	$$ R_t = \sum_{k=0}^{\infty} \gamma^k r_{t+k+1} $$	随机变量，表示从时刻 $t$ 开始实际路径的即时奖励的随机变量。与策略无关，反映实际路径
$$G_t$$	$$ G_t = \sum_{k=0}^{T-t-1} \gamma^k r_{t+k+1} $$	随机变量，是单条轨迹的实际观测值
$r(s, a)$	$$ r(s, a) = \mathbb{E}[r_{t+1}(s,a) \mid S_t = s, A_t = a] $$	标量函数，表示在状态 $s$ 执行动作 $a$ 后单步的期望即时奖励。
$Q^\pi(s, a)$	$$ Q^\pi(s, a) = \mathbb{E}_\pi[G_t	S_t = s, A_t = a] $$

---

• $R_t,r(s,a)$ 反映的是即时的奖励，$G_t,Q^\pi(s,a)$ 反映的是长期的奖励，$Q^\pi(s, a)$ 是 $G_t$ 的期望（固定 $s,a$，而 $V^\pi(s)$ 只固定 $s$），$r(s,a)$ 是 $R_t$ 的期望
• $R_t$ 和 $G_t$ 是单条轨迹的实际观测值，不可直接计算，理论推导的时候他们都会被求期望

最优策略的简化写法：

​ 由于学习目标是学习一个最优策略 $\pi^8$，因此很多指标在最优策略下有简写：

• 动作值函数 $Q^\pi(s,a)$ 在最优策略 $\pi^*$ 下的取值记为 $Q^*(s,a)$
• 状态值函数 $V^*(s)$ 在最优策略 $\pi^*$ 下的取值记为 $V^*(s)$
• 优势函数

其它记号：

$\mathbb{E}_{\text{Env}}$ 一般来说只是对状态转移取期望，此时会固定 $t$ 时刻的状态 $s_t$ 和动作 $a_t$，即：

$$\mathbb{E}_{\text{Env}} = \mathbb{E}_{s' \sim P(\cdot|s,a)}$$

$\mathbb{E}_{\pi}$ 一般来说是同时对动作选择和状态转移求期望，此时只固定 $t$ 时刻的状态 $s_t$，即要取二重的期望：

$$\mathbb{E}_{\pi} = \mathbb{E}_{s' \sim P(\cdot|s,a)}\mathbb{E}_{a \sim \pi(\cdot|s)}$$

• 值得一提的是强化学习中下标 $\pi$ 的含义，代表着后续的采样过程都遵循策略 $\pi$，但是在策略提升定理里面的记法除外，$\mathbb{E}_{\pi'}[R_t + \gamma V^\pi(S_{t+1}) | S_t = s]$ 中求期望的下标 $\pi'$ 这个策略只影响一步的采样，即 $t$ 时刻的动作 $a_t$ 的采样，后续执行的策略仍然是 $\pi$

基本概念：

模型：

​ 对环境的一种建模，给定一个状态和动作，模型能够预测下一个状态和奖励的分布：即 $p(s',r|s,a)$，模型一般可以分为两类，分布模型（distribution model）和样本模型（sample model）：

• 分布模型（distribution model）：描述轨迹的所有可能性和概率
• 样本模型（sample model）：根据概率进行采样，只产生一条可能的轨迹

模型的作用是得到模拟的经验数据，来帮助进行策略的规划

规划：

​ 输入一个模型和旧策略，输出一个新策略的过程称为规划：

graph LR
    A[输入模型] --> C[规划]
    B[旧策略] --> C
    C --> D[新策略]

规划分为状态空间的规划（state-space planning）和规划空间（plan-space planning）的规划：

• 状态空间的规划(state-space planning)：在状态空间搜索最佳策略，这是最常见的

• 规划空间的规划(plan-space planning)：在规划空间搜索最佳策略，包括遗传算法和偏序规划。这时，一个规划就是一个动作集合以及动作顺序的约束，这时的状态就是一个规划，目标状态就是能完成任务的规划