多臂老虎机

多臂老虎机问题

题目描述：

​ 有一个拥有 $K$ 根拉杆的老虎机(multi-armed bandit)，拉动每一根拉杆都对应一个关于奖励的概率分布 $\mathcal{R}$。我们每次拉动其中一根拉杆，就可以从该拉杆对应的奖励概率分布中获得一个奖励 $r$。我们在各根拉杆的奖励概率分布未知的情况下，从头开始尝试，目标是在操作 $T$ 次拉杆后获得尽可能高的累积奖励。由于奖励的概率分布是未知的， 因此我们需要在**“探索拉杆的获奖概率”和“根据经验选择获奖最多的拉杆”**中进行权衡。“采用怎样的操作策略才能使获得的累积奖励最高”便是多臂老虎机问题

多臂老虎机问题可以表示为一个元组 $\langle \mathcal{A,R} \rangle$ ，其中：

• $\mathcal{A}$ 为动作集合，其中一个动作表示拉动一根拉杆，若多臂老虎机一共有 $K$ 根拉杆，那 动作空间就是集合 $\{\boldsymbol {a_1, a_2, ..., a_k} \}$，我们用 $\boldsymbol a_t \in \mathcal{A}$ 表示任意一个动作
• $\mathcal{R}$ 为奖励概率分布，拉动每一根拉杆的动作 $a$ 都对应一个奖励概率分布 $\mathcal{R}(r \mid \boldsymbol a)$ ，拉动不同拉杆的奖励分布通常是不同的

​ 假设每个时间步只能拉动一根拉杆，多臂老虎机的目标为最大化一段时间步 $T$ 内累积的奖励： $\max \sum_{t=1}^{T} r_t, \ r_t \sim \mathcal{R}(\cdot \mid \boldsymbol a_t)$ 。其中 $\boldsymbol a_t$ 表示在第 $t$ 时间步拉动某一拉杆的动作，$r_t$ 表示动作 $\boldsymbol a_t$ 获得的奖励

​ 多臂老虎机问题没有环境状态的改变，没有 state transition 随机性带来的噪声，容易推各种策略算法的上界，具有理论意义，多臂老虎机问题的主要核心在于探索（exploration）与利用（exploitation）之间的 trade off

算法描述：

​ 对于每一个动作 $\boldsymbol a$，我们定义其期望奖励为 $Q(\boldsymbol a) = \mathbb{E}_{r \sim \mathcal{R}(\cdot \mid \boldsymbol a)} [r]$（没有状态的参与）。于是，至少存在一根拉杆，它的期望奖励不小于拉动其他任意一根拉杆，我们将该最优期望奖励表示为 $Q^* = \max_{\boldsymbol a \in \mathcal{A}} Q(\boldsymbol a)$。

​ 为了找出最优拉杆，算法的核心在于对黑盒模型内部信息的估计，这包含两个步骤：

1. 对同一根拉杆拉多次的回报估计
2. 决定探索新的拉杆还是选择已观测到的最优的拉杆，即策略算法

估计已有的拉杆：

​ 为了知道拉动哪一根拉杆能获得更高的奖励，我们需要估计拉动这根拉杆的期望奖励。由于只拉动一次拉杆获得的奖励存在随机性，所以需要多次拉动一根拉杆，然后计算得到的多次奖励的期望，其算法流程如下所示

对于 $ \forall \boldsymbol a \in \mathcal{A}$，初始化计数器 $N(\boldsymbol a)=0 $ 和期望奖励估值 $\hat{Q}(\boldsymbol a)=0$

for t = 1 to T do
选取某根拉杆，该动作记为 $ a_t $
得到奖励 $ r_t $
更新计数器： $ N(a_t) = N(a_t) + 1 $
更新期望奖励估值： $ \hat Q(a_t) = \hat Q(a_t) + \frac{1}{N(a_t)}[r_t - \hat Q(\boldsymbol a_t)] $
end for

由以下公式导出：

Q_k = \frac{1}{k} \underset{i=1} {\overset {T}\sum} r_i = \frac{1}{k}\left( r_k + \underset{i=1} {\overset {T-1}\sum} r_i = \frac{1}{k}\right) \\ = Q_{k-1} + \frac{1}{k}[r_k -Q_{k-1}]

策略算法实现：探索新的拉杆

​ 为了观察拉动一根拉杆的期望奖励离最优拉杆期望奖励的差距，引入愧悔（regret）概念。懊悔被定义为拉动当前拉杆的动作 $\boldsymbol a$ 与最优拉杆的期望奖励差，即 $ R(\boldsymbol a)=Q^*−Q(\boldsymbol a)$。累积懊悔（cumulative regret）即操作 $T$ 次拉杆后累积的懊悔总量，对于一次完整的 $T$ 步决策 $\{\boldsymbol {a_1, a_2, ..., a_T} \}$，累积懊悔为 $\sigma_R = \sum_{t=1}^T R(\boldsymbol a_i)$。MAB 问题的目标为最大化累积奖励，等价于最小化累积懊悔

​ 考虑探索（exploration）与利用（exploitation）之间的 trade off：

• 如果探索占比为 100%，则每次决策都不是最优决策，因此累计懊悔的增长速度是 $O(T)$
• 如果利用占比为 100%，在没有搜索到最优决策的情况下每次做的都是次优决策，因此累计懊悔的增长速率仍为 $O(T)$

因此做到探索和利用之间的 balance 是非常重要的

​ 设计策略时就需要平衡探索和利用的次数，使得累积奖励最大化。一个比较常用的思路是在开始时做比较多的探索，在对每根拉杆都有比较准确的估计后， 再进行利用

探索策略的一些方法主要有下面集中：

• Naive Exploration：比如 $\epsilon$-greedy，$\epsilon$-greedy 衰减等
• Optimistic Initialization：积极初始化，其实不是一种真正的探索算法，容易收敛到局部最优解
• Uncertainty Measurement：将不确定性度量也纳入收益中
• Probability Matching
• State Searching：是在 alpha go 中使用的一种技术

$\epsilon$ -Greedy：

​ 完全贪婪算法即在每一时刻采取期望奖励估值最大的动作（拉动拉杆），这就是纯粹的利用， 而没有探索，所以我们通常需要对完全贪婪算法进行一些修改，强化学习中最 naive 和常用的探索算法为 $\epsilon$ -贪婪 （$\epsilon$ -Greedy）。它在完全贪婪算法的基础上添加了噪声，每次以概率$1−\epsilon$ 选择以往经验中期望奖励估值最大的那根拉杆（利用），以概率 $\epsilon$ 随机选择一根拉杆（探索）

$$\boldsymbol{a}_t =\left\{ \begin{array}{c} \arg\underset{\boldsymbol{a}\in \mathcal{A}}{\max}\hat Q(\boldsymbol a) \ &\text{sample probability:}\ 1-\epsilon \\ \text{sample from} \mathcal{A} &\text{sample probability} \ \epsilon \\ \end{array} \right.$$

​ 随着探索次数的不断增加，我们对各个动作的奖励估计得越来越准，此时就没必要继续花大力气进行探索。所以具体实现中，我们可以令 $\epsilon$ 随时间衰减。但是请注意，$\epsilon$ 不会在有限的步数内衰减至 0，因为基于有限步数观测的完全贪婪算法仍然是一个局部信息的贪婪算法，永远距离最优解有一个固定的差距

Uncertainty Measurement：

UCB 算法:

​ 将不确定性度量也纳入收益中，综合考虑现有的期望奖励估值和不确定性，设 $U(\boldsymbol a)$ 为动作 $\boldsymbol a$ 探索的信息收益。经验性的：如果 $N(\boldsymbol a)$ 大则 $U(\boldsymbol a)$ 小，则策略可以写为：

$$\pi: \boldsymbol a = \arg\max_{a \in \mathcal{A}} Q(\boldsymbol a) + U(\boldsymbol a)$$

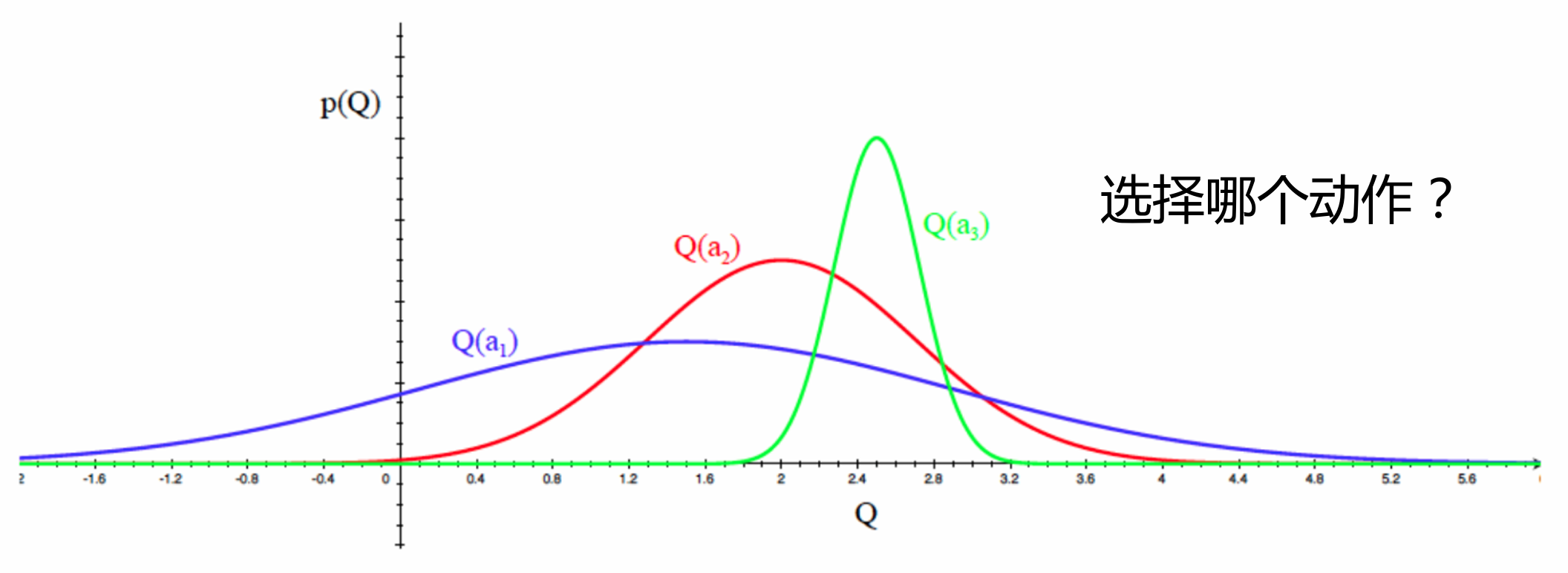
​ 上置信界（upper confidence bound，UCB）算法是一种经典的基于不确定性的策略算法， 它用到了霍夫丁不等式（Hoeffding’s inequality）：

​ 令 $X_1, X_2, ..., X_n$ 为 $n$ 个独立同分布的随机变量，取值范围为 $[0,1]$，其经验期望为 $\bar x_n = \frac{1}{n} \sum_{j=1}^n X_j$ ，则有：

$$P(E[x] \geq \bar x_t + u) \leq e^{-2nu^2}$$

但是需要注意的是，这里的 UCB 算法其实内在是一种白盒算法，我们是知道老虎机的分布是伯努利分布了，因此越不确定的算法它的概率分布越“扁平”，但是对于一般的情况，概率分布可能就是很扁平的，那么这样的算法肯定是不适用的

Thompson Sampling：

​ 这个算法的想法十分简单，估计每个老虎机采样的概率分布，从每个概率分布内直接采样，按照采样值进行排序，用采样值最高的老虎机序号来执行动作，因此汤普森采样是一种计算所有拉杆的最高奖励概率的蒙特卡洛采样方法

​

​ 使用 Thompson Sampling 方法的核心就是估计概率分布，而且要让奖励概率分布在过程中进行更新，因此用来建模的概率分布最好需要适合递推，在实际中常常采用 $\beta$ 分布来进行递推（其实也是一种内在的白盒算法）