einops 和 einsum 的使用——einsum
einsum是一个强大的执行爱因斯坦求和约定的函数,他几乎可以进行张量的所有运算,加上改变张量形状的einops库,它们可以使代码更加易读。它们的主要区别如下:
- 表达能力:
einops 提供了更广泛的张量操作,包括但不限于求和。它可以用于重排、合并、拆分等各种操作,使得代码更具灵活性einsum 主要用于执行张量的求和操作,虽然可以通过合适的字符串表示式执行其他操作,但相对而言,其表达能力不如 einops 多样
- 直观性:
einops 的语法更加直观,它使用一些关键词来描述张量操作,使得代码更易读。einsum 使用字符串表示式,这种表示方式相对于einops比较难懂
- 性能:
- 在一些情况下,
einops 可能在性能上稍逊于 einsum。einsum 的实现经过了高度优化,特别是在使用NumPy等库时,它可以通过C语言加速执行,因此在某些情况下可能更快
- 使用场景:
einops 更适合需要进行各种复杂张量操作的情况,特别是需要频繁改变张量形状的情况einsum 更适合执行相对简单的张量求和操作,尤其是对于数学上常见的张量运算。
einsum的用法:
einsum实现矩阵乘法的例子:
1
2
3
4
| a = torch.rand(2,3)
b = torch.rand(3,4)
c = torch.einsum("ik,kj->ij", [a, b])
|
einsum 的第一个参数 “ik,kj->ij”,该字符串(下文以 equation 表示)表示了输入和输出张量的维度。equation 中的箭头左边表示输入张量,以逗号分割每个输入张量,箭头右边则表示输出张量。表示维度的字符只能是26个英文字母 ‘a’ - ‘z’。
而 einsum 的第二个参数表示实际的输入张量列表,其数量要与 equation 中的输入数量对应。同时对应每个张量的 子 equation 的字符个数要与张量的真实维度对应,比如 “ik,kj->ij” 表示输入和输出张量都是两维的。
基本规则:
- 规则一,equation 箭头左边,在不同输入之间重复出现的索引表示,把输入张量沿着该维度做乘法操作,以上面矩阵乘法为例, “ik,kj->ij”,k 在输入中重复出现,所以就是把 a 和 b 沿着 k 这个维度作相乘操作
- 规则二,只出现在 equation 箭头左边的索引,表示中间计算结果需要在这个维度上求和,也就是上面提到的求和索引
- 规则三,equation 箭头右边的索引顺序可以是任意的,比如上面的 “ik,kj->ij” 如果写成 “ik,kj->ji”,那么就是返回输出结果的转置,用户只需要定义好索引的顺序,转置操作会在 einsum 内部完成
特殊规则
特殊规则有两条:
- equation 可以不写包括箭头在内的右边部分(不推荐),那么在这种情况下,输出张量的维度会根据默认规则推导。就是把输入中只出现一次的索引取出来,然后按字母表顺序排列,比如上面的矩阵乘法 “ik,kj->ij” 也可以简化为 “ik,kj”,根据默认规则,输出就是 “ij” 与原来一样;
- equation 中支持 “…” 省略号(不推荐),用于表示并不关心的索引,比如只对一个高维张量的最后两维做转置可以这么写:
1
2
3
| a = torch.randn(2,3,5,7,9)
b = torch.einsum('...ij->...ji', [a])
|
矩阵转置:
Bji=Aij
1
2
| a = torch.arange(6).reshape(2, 3)
torch.einsum('ij->ji', [a])
|
求和
b=i∑j∑Aij
1
2
| a = torch.arrange(6).reshape(2, 3)
torch.einsum('ij->', [a])
|
点积
c=i∑aibi
1
2
3
| a = torch.arrange(3)
b = torch.arrange(3, 6)
torch.einsum('i,i->', [a, b])
|
Hardmard积
Cij=AijBij
1
2
3
| a = torch.arrange(6).reshape(2, 3)
b = torch.arrange(6, 12).reshape(2, 3)
torch.einsum('ij,ij->ij', [a, b])
|
外积
Cij=aibj
1
2
3
| a = torch.arrange(3)
b = torch.arrange(3, 7)
torch.einsum('i,j->ij', [a, b])
|
batch矩阵相乘
Cijl=k∑AijkAikl
1
2
3
| a = torch.randn(3,2,5)
b = torch.randn(3,5,3)
torch.einsum('ijk,ikl->ijl', [a, b])
|
张量缩约(上面例子的一般版本)
Cpstuv=q∑r∑ApqrsBtuqvr
注意:在相乘维度上元素个数一定要相同
1
2
3
4
| a = torch.randn(2,3,5,7)
b = torch.randn(11,13,3,17,5)
torch.einsum('pqrs,tuqvr->pstuv', [a, b]).shape
torch.Size([2, 7, 11, 13, 17])
|
双线性变换(einsum可用于超过两个张量的计算)
Dij=k∑l∑AikBjklAil
1
2
3
4
| a = torch.randn(2,3)
b = torch.randn(5,3,7)
c = torch.randn(2,7)
torch.einsum('ik,jkl,il->ij', [a, b, c])
|
案例
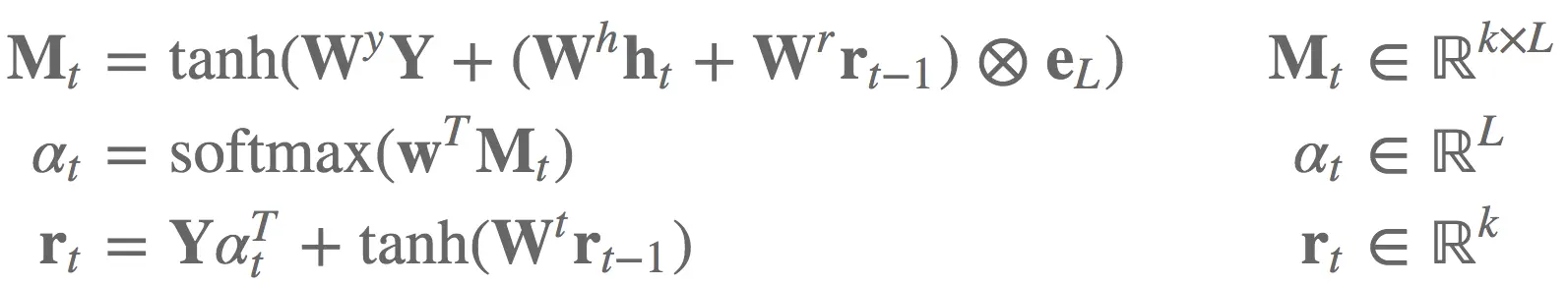
用传统写法实现这些可要费不少力气,特别是考虑batch实现。einsum是我们的救星!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
bM, br, w = random_tensors([7], num=3, requires_grad=True)
WY, Wh, Wr, Wt = random_tensors([7, 7], num=4, requires_grad=True)
def attention(Y, ht, rt1):
tmp = torch.einsum("ik,kl->il", [ht, Wh]) + torch.einsum("ik,kl->il", [rt1, Wr])
Mt = F.tanh(torch.einsum("ijk,kl->ijl", [Y, WY]) + tmp.unsqueeze(1).expand_as(Y) + bM)
at = F.softmax(torch.einsum("ijk,k->ij", [Mt, w]))
rt = torch.einsum("ijk,ij->ik", [Y, at]) + F.tanh(torch.einsum("ij,jk->ik", [rt1, Wt]) + br)
return rt, at
Y = random_tensors([3, 5, 7])
ht, rt1 = random_tensors([3, 7], num=2)
rt, at = attention(Y, ht, rt1)
|
总结
einsum是一个函数走天下,用例中可以看到,我们仍然需要在einsum之外应用非线性和构造额外维度。类似地,分割、连接、索引张量仍然需要应用其他库函数(einiops就是很好的选择)。
使用einsum的麻烦之处是你需要手动实例化参数,操心它们的初始化