Affinity-Aware Upsampling
相似度(affinity)在稠密预测任务中是一个非常重要的信息,二阶的特征常用于建立相似度信息,本文主要工作是将原有的动态上采样过程都总结成一阶的信息,并在此基础上提出使用二阶的信息,用此将自相似性引入采样过程,同时通过低秩双线性模型减少模型参数,降低模型计算开支
另一种将Upsampling算子统一的视角:
对于一个单通道的feature map Z∈Rk×k ,目标是通过 Z 去产生一个新的像素值(upsampled feature point),将 Z 向量化为 z∈Rk2×1,同时设上采样算子 W∈Rk×k 向量化为 w∈Rk2×1,则现有的上采样算子的形式可以统一为 g(w,z)=wTz (对应新的feature map中一个像素点)
文章中将现有的上采样算子分为了两类:
distance-based Upsampling
基于位置信息的上采样算子,例如最临近插值
feature-based Upsampling
基于图像内容信息的上采样算子,例如CARAFE,max upooling,IndexNet
可以看出无论哪种采样算子都是 g(w,z)=wTz 的形式
Learning Affinity-Aware Upsampling
现有一个feature map M∈RC×H×W,目标为产生大小为 M′∈RC×rH×rW 的新feature map,对于M′ 中每一点(设为 (i,j) 位置处),我们都要去学习一个上采样核 w∈Rk2×1 ,则将 w 与原图像对应点(⌊ri⌋,⌊rj⌋)邻域内的图像信息经过 g(w,z)=wTz 则可得新feature map (i,j) 位置处的像素值
本文Affinity 定义:
对于 l 和其他所有可能位置 p 之间的Affinity定义为:
∀psoftmax(sim(ml,mp))
相似度直接采用内积的方式定义:
sim(ml,mp)=mlTmp
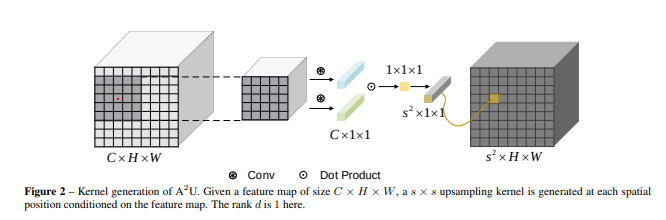
上采样算子的生成:
设原 local feature map(注意这个定义,它是目标采样点的邻域!!!)为 X∈RC×h1×w1 ,将其每一个关于通道切片向量化为X∈RC×N ,其中N=h1×w1 ,我们的目标是基于X 产生一个上采样算子,下面我们利用Affinity去进行上采样,我们不使用一阶的信息构建 $w = \sum_{i = 1}^C \sum_{j = 1}^N a_{ij} x_{ij} $,因为二阶的信息常常用于构建相似度,使用类似于transfomer中的二阶信息(QKV矩阵):为了编码二阶的信息,我们的想法是利用双线性插值,设另外一个feature map y∈RC×h2×w2,同样将其向量化为Y∈RC×M,M=h2×w2,yi∈RC×1xi∈RC×1
w=i=1∑Nj=1∑Maijψ(xi)Tϕ(yi)=k=1∑Ci=1∑Nj=1∑Maijqkxiktkyjk=k=1∑Ci=1∑Nj=1∑Maijkxikyjk=k=1∑CXkAkYk
其中 ϕ 和 ψ 为embedding function,$\mathscr{a}{ijk}=a{ij}q_kt_k $ ,Xk∈RN×1 Yk∈RM×1Ak∈RN×M , 是第k层feature map的affinity matrix。
Ak∈RN×M 参数量非常大而且难以训练,为了减少参数量且将计算过程变为卷积形式,我们引入假设:rank(Ak)≤d ,则可以分解为Ak=UkVKT ,$ \boldsymbol U_k \in \mathbb{R}^{N \times d},\boldsymbol V_k \in \mathbb{R}^{M \times d}$,因此上式可变形为:
w=k=1∑CxkUkVkTyk=k=1∑C1TUkTxk⊙VkTyk=1Tk=1∑CUkTxk⊙VkTyk
其中 ⊙ 代表Hadmard积,列向量 1∈Rd×1
因为我们要生成 s×s 大小的上采样核,则列向量 1 可写为 P∈Rd×s2 ,则**W向量化之后的采样核 w** 可以写为:
w=PTk=1∑CUkTxk⊙VkTyk=PTr=1catd(k=1∑C(ukrTxk⊙vkrTyk))=PTr=1catd(gconv(Ur,X)⊙gconv(Vr,Y))=conv(P,r=1catd(gconv(Ur,X)⊙gconv(Vr,Y)))
其中ukr∈RN×1,vkr∈RM×1,卷积核P∈Rd×s2×1×1,U∈Rd×C×h1×w1,V∈Rd×C×h2×w2 都是 P∈RN×d×1,U∈RN×d×C,V∈RN×d×C 的reshaped tensor,conv(K,M) 代表在使用kernal K 在feature map M 上使用卷积操作,gconv代表group convolution,且 groups 的个数为 C,至此,我们将一个新的算子化为了能用高效的 einsum 操作的形式
补充:
- X,Y 可以选择相同也可以选择不同,本文选择 X=Y,这样就对应着 self attention 中的自相似性
- rank d 的范围可以在 [1,min(N,M)] 内选取,本文令 d=1
- U,V 就可以视为 encoding function,为了补偿低秩模型导致的参数量过小的情况,本文选取动态生成 U,V,它们的参数可以根据模型复杂度选择:共享参数,不共享参数,半共享参数,本文中 U,V 的生成过程为:先通过一次平均值池化之后,在通过一次 1×1 的卷积生成
与下采样算子融合
类似于IndexNet,upsampling可以extend to downsampling,我们使用相同的 U,V 在上下采样操作中,但是使用不同的 P 考虑到采样核的大小不同。即上采样核 Wu 大小为 Su2×H×W, 下采样核$\mathcal{W}_d $ 大小为 Sd2×H/r×W/r ,本文中令 sd2=r2Su
一些经验:
- high-resolution feature map(图像大的)对于提取spatial information来说更加有效
- 二阶的特征比一阶特征在恢复spatial details更加有效
网络设计:
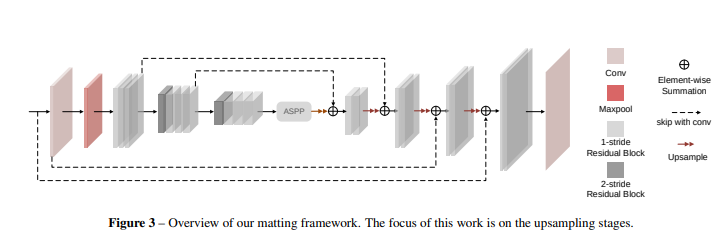
整个网络沿用了UNet的结构,(没看懂A2U在哪里)
Q:the pairwise similarity is damaged during upsampling?

